Wzór Na Pole Wycinka Koła

W geometrii, wycinek koła stanowi fundamentalną figurę, a obliczenie jego pola jest kluczowe w wielu zastosowaniach, od inżynierii po grafikę komputerową. Zrozumienie wzoru na pole wycinka koła pozwala na precyzyjne kalkulacje w różnorodnych kontekstach. W tym artykule przyjrzymy się temu wzorowi, jego pochodzeniu, zastosowaniom oraz przedstawimy przykłady, które pomogą zrozumieć jego praktyczne znaczenie.

Definicja i podstawowe pojęcia

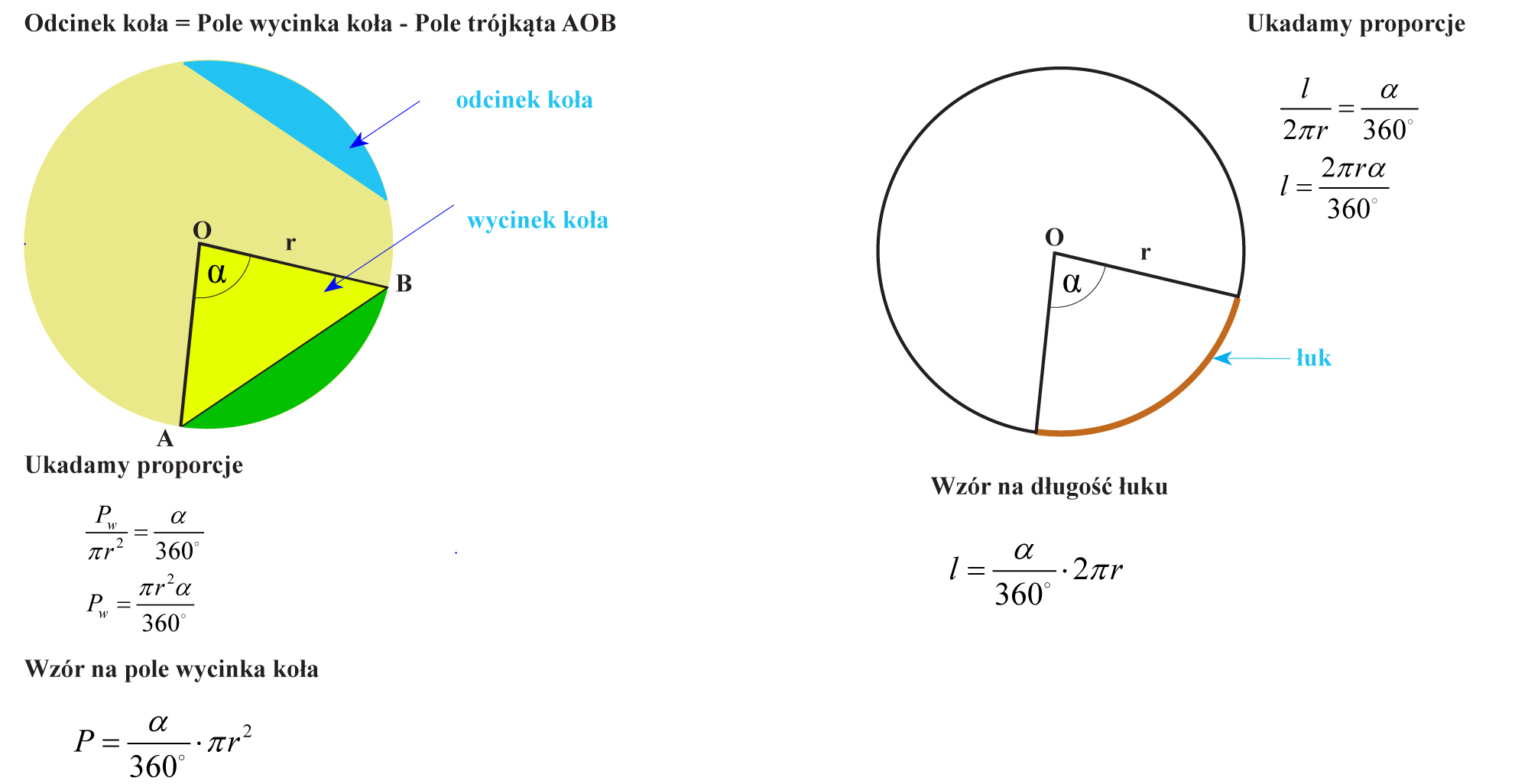
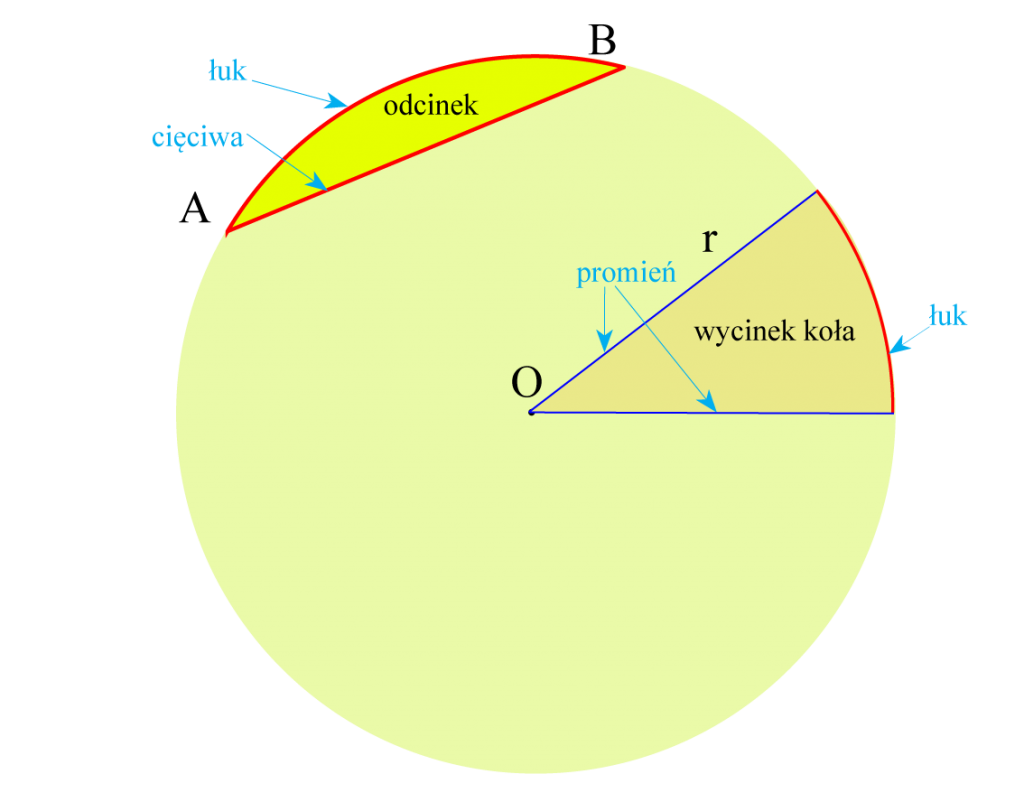
Zanim przejdziemy do samego wzoru, warto ugruntować naszą wiedzę o podstawowych pojęciach. Koło to zbiór wszystkich punktów na płaszczyźnie, które znajdują się w równej odległości od ustalonego punktu, zwanego środkiem koła. Odległość ta to promień (r). Wycinek koła to część koła ograniczona dwoma promieniami i łukiem między nimi.

Kluczowym elementem wycinka koła jest kąt środkowy (α), który jest kątem między dwoma promieniami tworzącymi wycinek. Kąt ten może być wyrażony w stopniach lub radianach, co ma wpływ na postać wzoru na pole wycinka.

Wyrażanie kąta w stopniach i radianach

Stopnie to popularna jednostka miary kątów, gdzie pełny kąt (pełny obrót) ma 360 stopni. Z kolei radian to miara kąta środkowego oparta na długości łuku wycinka. Definiuje się go jako kąt, dla którego długość łuku wycinka jest równa promieniowi koła. Pełny kąt w radianach wynosi 2π.

Przeliczanie między stopniami a radianami odbywa się za pomocą prostej proporcji:

α (rad) = α (stopnie) * (π / 180)

α (stopnie) = α (rad) * (180 / π)

Wzór na pole wycinka koła

Pole wycinka koła można obliczyć za pomocą dwóch podstawowych wzorów, w zależności od tego, czy kąt środkowy jest podany w stopniach, czy w radianach.

Wzór z kątem w stopniach

Jeśli kąt środkowy α jest wyrażony w stopniach, to wzór na pole wycinka koła wygląda następująco:

P = (α / 360) * πr²

Gdzie:

P to pole wycinka koła.
α to kąt środkowy wyrażony w stopniach.
r to promień koła.
π (pi) to stała matematyczna, w przybliżeniu równa 3.14159.

Ten wzór opiera się na proporcji. Pole wycinka koła stanowi pewną część pola całego koła (πr²), a ta część jest określona przez stosunek kąta środkowego wycinka do pełnego kąta (360 stopni).

Wzór z kątem w radianach

Jeśli kąt środkowy α jest wyrażony w radianach, to wzór na pole wycinka koła upraszcza się do:

P = (1/2) * α * r²

Gdzie:

P to pole wycinka koła.
α to kąt środkowy wyrażony w radianach.
r to promień koła.

Wzór ten jest bardziej elegancki i często używany w obliczeniach matematycznych i fizycznych, ponieważ radian jest naturalną jednostką miary kątów.

Pochodzenie wzoru

Wzór na pole wycinka koła wyprowadza się z proporcji. Pole wycinka jest proporcjonalne do kąta środkowego, jaki ten wycinek obejmuje. Rozważmy całe koło, którego pole wynosi πr², a kąt środkowy wynosi 360 stopni (lub 2π radianów). Wtedy:

Dla stopni: P / πr² = α / 360 => P = (α / 360) * πr²

Dla radianów: P / πr² = α / 2π => P = (α / 2π) * πr² = (1/2) * α * r²

Powyższe równania pokazują, jak wyprowadzić wzór na pole wycinka z podstawowych zasad geometrii.

Przykłady zastosowań

Wzór na pole wycinka koła znajduje zastosowanie w wielu dziedzinach. Poniżej kilka przykładów:

Architektura i inżynieria

W architekturze, obliczenia pola wycinka koła są niezbędne przy projektowaniu okien, łuków i innych elementów o kształcie kołowym. Inżynierowie wykorzystują ten wzór przy projektowaniu mostów, tuneli i innych konstrukcji inżynieryjnych.

Grafika komputerowa

W grafice komputerowej, wycinki koła są często używane do tworzenia różnych kształtów i efektów wizualnych. Obliczenie ich pola pozwala na precyzyjne pozycjonowanie i skalowanie elementów graficznych.

Matematyka i fizyka

W matematyce i fizyce, wzór na pole wycinka koła jest wykorzystywany w wielu równaniach i modelach, np. przy obliczaniu powierzchni obszarów ograniczonych krzywymi, czy przy analizie ruchu po okręgu.

Przemysł spożywczy

Wyobraźmy sobie fabrykę produkującą ciasta w kształcie wycinków koła. Obliczenie pola każdego wycinka pozwala na dokładne dozowanie składników, co przekłada się na oszczędność i równomierność produktu.

Dane geograficzne

Podczas analizy map i danych geograficznych, obliczanie pola wycinków koła może być przydatne do szacowania obszarów zajmowanych przez określone struktury, takie jak obszary irygacyjne w kształcie wycinków koła.

Przykład obliczeniowy

Załóżmy, że mamy wycinek koła o promieniu r = 5 cm i kącie środkowym α = 60 stopni. Chcemy obliczyć jego pole.

1. Używamy wzoru z kątem w stopniach:

P = (α / 360) * πr² = (60 / 360) * π * 5² = (1/6) * π * 25 ≈ 13.09 cm²

Teraz załóżmy, że kąt jest podany w radianach: α = π/3 rad. (π/3 rad = 60 stopni)

2. Używamy wzoru z kątem w radianach:

P = (1/2) * α * r² = (1/2) * (π/3) * 5² = (1/2) * (π/3) * 25 = (25π) / 6 ≈ 13.09 cm²

Otrzymaliśmy taki sam wynik, co potwierdza poprawność obu wzorów.

Wskazówki i uwagi

Zawsze upewnij się, w jakiej jednostce (stopnie czy radiany) podany jest kąt środkowy. Użycie niewłaściwego wzoru doprowadzi do błędnych wyników.
Pamiętaj o jednostkach. Jeśli promień jest podany w centymetrach, to pole wycinka będzie wyrażone w centymetrach kwadratowych.
W praktycznych obliczeniach, wartość π można przybliżyć do 3.14159 lub skorzystać z funkcji π w kalkulatorze.

Alternatywne metody obliczania

Chociaż wzory przedstawione powyżej są najczęściej używane, istnieją sytuacje, w których możemy skorzystać z innych metod.

Jeżeli znamy długość łuku (l) wycinka koła i jego promień (r), to pole wycinka możemy obliczyć za pomocą wzoru:

P = (1/2) * l * r

Ten wzór wynika bezpośrednio z zależności między długością łuku, kątem środkowym i promieniem: l = α * r (gdzie α jest w radianach). Podstawiając to do wzoru P = (1/2) * α * r², otrzymujemy P = (1/2) * l * r.

Podsumowanie

Wzór na pole wycinka koła jest fundamentalnym narzędziem w geometrii i znajduje szerokie zastosowanie w różnych dziedzinach. Rozumienie jego pochodzenia, poprawne stosowanie oraz świadomość jednostek miar są kluczowe do precyzyjnych obliczeń.

Zachęcamy do eksperymentowania z różnymi wartościami promienia i kąta środkowego, aby lepiej zrozumieć, jak zmienia się pole wycinka koła. Spróbuj rozwiązać kilka zadań praktycznych, aby utrwalić zdobytą wiedzę. Pamiętaj, ćwiczenie czyni mistrza!