Wzór Na Pole Trójkata Z Boków

Czy kiedykolwiek zastanawiałeś się, jak obliczyć powierzchnię trójkąta, znając tylko długości jego boków? To pytanie, które może pojawić się na lekcji matematyki, w projekcie architektonicznym, a nawet podczas planowania ogrodu. Na szczęście istnieje eleganckie rozwiązanie – wzór Herona. Ten artykuł jest przeznaczony dla uczniów, studentów, amatorów matematyki i każdego, kto szuka praktycznego sposobu na obliczenie pola trójkąta bez znajomości jego wysokości czy kątów.

Wprowadzenie do Wzoru Herona

Wzór Herona, nazwany na cześć greckiego matematyka i inżyniera Herona z Aleksandrii, pozwala obliczyć pole trójkąta znając tylko długości jego trzech boków. To potężne narzędzie, zwłaszcza w sytuacjach, gdzie inne metody, takie jak klasyczny wzór (pole = 1/2 * podstawa * wysokość) są trudne do zastosowania, ponieważ nie znamy wysokości trójkąta.

Klasyczny wzór na pole trójkąta wymaga znajomości długości podstawy i wysokości opuszczonej na tę podstawę. Czasami jednak mamy dostęp tylko do długości boków. Wtedy z pomocą przychodzi wzór Herona. Jest on szczególnie przydatny w geometrii, inżynierii i architekturze, gdzie dokładne obliczenia powierzchni są kluczowe.

Co Potrzebujesz Wiedzieć?

Zanim przejdziemy do samego wzoru, upewnijmy się, że rozumiemy kilka podstawowych pojęć:

Boki trójkąta: Trójkąt ma trzy boki, oznaczmy je jako a, b i c.
Półobwód: Półobwód trójkąta to połowa sumy długości wszystkich jego boków. Oznaczamy go jako p.

Wzór Herona – Krok po Kroku

Teraz, gdy mamy już jasność co do podstawowych pojęć, możemy przejść do samego wzoru Herona:

Pole trójkąta (P) = √[p(p-a)(p-b)(p-c)]

Gdzie:

P to pole trójkąta
a, b, c to długości boków trójkąta
p to półobwód trójkąta, obliczany jako: p = (a + b + c) / 2

Aby zastosować wzór Herona, wykonaj następujące kroki:

Oblicz półobwód (p): Dodaj długości wszystkich trzech boków trójkąta (a + b + c) i podziel wynik przez 2.
Oblicz różnice (p-a), (p-b), (p-c): Odejmij od półobwodu długość każdego z boków.
Pomnóż wyniki: Pomnóż półobwód (p) przez wszystkie trzy różnice: p * (p-a) * (p-b) * (p-c).
Oblicz pierwiastek kwadratowy: Oblicz pierwiastek kwadratowy z otrzymanego wyniku. To da Ci pole trójkąta (P).

Przykład Praktyczny

Załóżmy, że mamy trójkąt o bokach długości: a = 5 cm, b = 6 cm i c = 7 cm. Obliczmy jego pole, stosując wzór Herona:

Oblicz półobwód (p): p = (5 + 6 + 7) / 2 = 9 cm
Oblicz różnice:
- p - a = 9 - 5 = 4 cm
- p - b = 9 - 6 = 3 cm
- p - c = 9 - 7 = 2 cm
Pomnóż wyniki: 9 * 4 * 3 * 2 = 216
Oblicz pierwiastek kwadratowy: √216 ≈ 14.7 cm²

Zatem pole trójkąta o bokach 5 cm, 6 cm i 7 cm wynosi około 14.7 cm².

Dlaczego Wzór Herona Działa?

Wzór Herona może wydawać się magiczny, ale jego działanie opiera się na solidnych podstawach matematycznych. Dowód wzoru Herona zazwyczaj wykorzystuje trygonometrię i twierdzenie Pitagorasa. Można go wyprowadzić, stosując prawo cosinusów do wyrażenia cosinusa jednego z kątów trójkąta w terminach długości boków, a następnie wykorzystując to do obliczenia sinusa tego kąta. Na koniec, używając standardowego wzoru na pole trójkąta (1/2 * ab * sin(C)), gdzie C jest kątem między bokami a i b, można dojść do wzoru Herona. Dokładny dowód jest nieco złożony i przekracza zakres tego artykułu, ale ważne jest, aby zrozumieć, że wzór ten ma solidne podstawy teoretyczne.

Zalety i Ograniczenia Wzoru Herona

Zalety:

Uniwersalność: Działa dla każdego trójkąta, niezależnie od jego kształtu (ostrokatny, prostokątny, rozwartokątny).
Wymagana tylko znajomość boków: Nie potrzebujesz znać wysokości ani kątów.
Stosunkowo prosty w użyciu: Kroki są jasne i łatwe do zapamiętania.

Ograniczenia:

Wymaga dokładnych pomiarów boków: Niedokładne pomiary mogą prowadzić do błędnych wyników.
Może być mniej intuicyjny niż klasyczny wzór: Dla niektórych osób klasyczny wzór (1/2 * podstawa * wysokość) może być łatwiejszy do zrozumienia.

Praktyczne Zastosowania Wzoru Herona

Wzór Herona znajduje szerokie zastosowanie w różnych dziedzinach:

Geodezja i Kartografia: Obliczanie powierzchni działek o nieregularnych kształtach.
Architektura i Inżynieria: Obliczanie powierzchni dachów, fasad i innych elementów konstrukcyjnych.
Projektowanie Ogrodów: Obliczanie powierzchni rabat kwiatowych i trawników.
Gry Komputerowe: Obliczanie powierzchni trójkątów w grafice 3D.

Wyobraź sobie, że projektujesz ogród i chcesz stworzyć rabatę kwiatową w kształcie trójkąta. Znasz długości boków rabaty, ale nie wiesz, jaka jest jej wysokość. Dzięki wzorowi Herona możesz łatwo obliczyć powierzchnię rabaty i oszacować, ile ziemi i roślin potrzebujesz.

Wzór Herona a Twierdzenie Pitagorasa

Warto zauważyć, że w przypadku trójkąta prostokątnego, możemy również skorzystać z twierdzenia Pitagorasa, aby znaleźć brakujący bok, a następnie użyć klasycznego wzoru na pole trójkąta. Jednak wzór Herona jest bardziej uniwersalny, ponieważ działa dla każdego trójkąta, niezależnie od jego kątów.

Alternatywne Metody Obliczania Pola Trójkąta

Oprócz wzoru Herona istnieją inne metody obliczania pola trójkąta, w zależności od dostępnych danych:

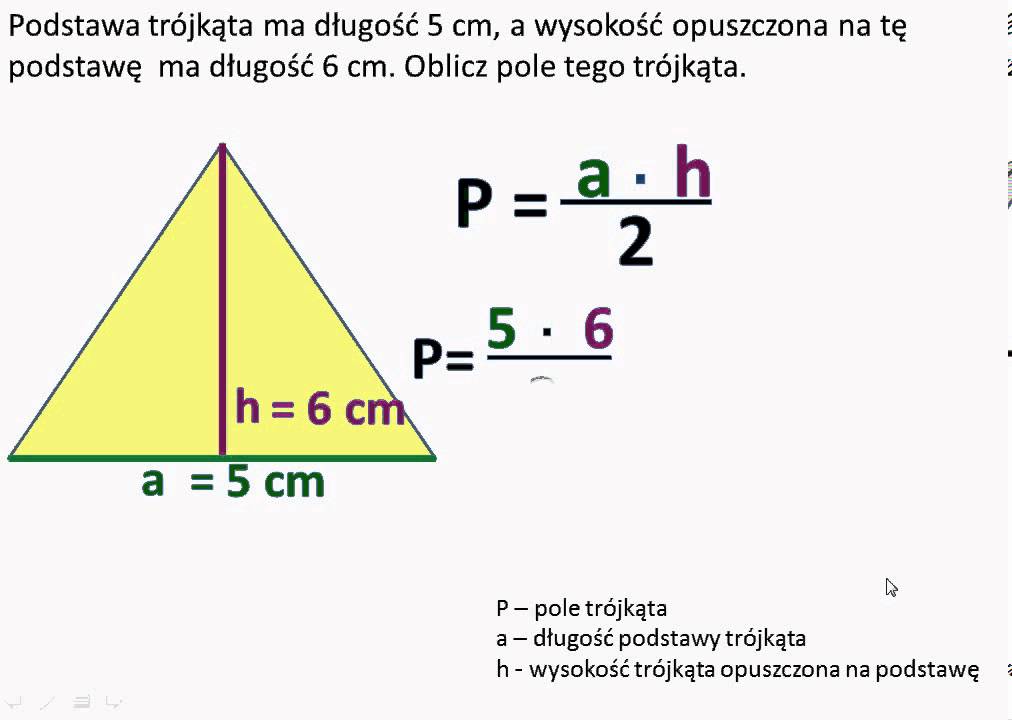
Klasyczny wzór: P = 1/2 * podstawa * wysokość
Wzór z użyciem dwóch boków i kąta między nimi: P = 1/2 * a * b * sin(C), gdzie a i b to długości boków, a C to kąt między nimi.
Wzór z użyciem współrzędnych wierzchołków: Jeśli znamy współrzędne wierzchołków trójkąta w układzie kartezjańskim, możemy użyć wzoru determinantowego.

Wybór odpowiedniej metody zależy od tego, jakie informacje posiadamy na temat trójkąta.

Podsumowanie i Wartość Dodana

Wzór Herona jest potężnym i uniwersalnym narzędziem do obliczania pola trójkąta, szczególnie przydatnym, gdy znamy tylko długości jego boków. Jego zastosowania są szerokie i obejmują różne dziedziny, od geometrii i inżynierii po projektowanie ogrodów i gry komputerowe.

Dzięki temu artykułowi poznałeś wzór Herona, nauczyłeś się go stosować krok po kroku, zrozumiałeś jego zalety i ograniczenia oraz odkryłeś jego praktyczne zastosowania. Mam nadzieję, że ta wiedza okaże się przydatna w Twoich dalszych studiach i projektach. Pamiętaj, że matematyka jest wszędzie wokół nas, a zrozumienie podstawowych wzorów i zasad może otworzyć drzwi do fascynującego świata logicznego myślenia i rozwiązywania problemów.

Zachęcam Cię do dalszego zgłębiania wiedzy matematycznej i poszukiwania nowych, inspirujących zastosowań wzoru Herona w Twoim życiu. Powodzenia!