Wzór Na Pole Trójkata Równobocznego Wpisanego W Okrąg

No dobrze, porozmawiajmy o wzorze na pole trójkąta równobocznego wpisanego w okrąg! Postaram się to wytłumaczyć prosto i zrozumiale.

Wyobraź sobie okrąg. Narysuj go sobie na kartce, albo po prostu pomyśl o nim. Teraz spróbuj wpisać w ten okrąg trójkąt równoboczny. To znaczy, że wszystkie wierzchołki tego trójkąta muszą leżeć na okręgu. Zwróć uwagę, że taki trójkąt będzie symetryczny względem środka okręgu.

No i teraz pojawia się pytanie: jak obliczyć pole takiego trójkąta, znając promień okręgu, w który jest wpisany? Mamy na to pewien wzór, który zaraz omówimy. Najpierw jednak, przypomnijmy sobie podstawowe rzeczy.

Podstawowy wzór na pole trójkąta (jakiegokolwiek!) to połowa iloczynu długości podstawy i wysokości: P = (1/2) * a * h, gdzie a to długość podstawy, a h to wysokość trójkąta opuszczona na tę podstawę. Dla trójkąta równobocznego, można ten wzór uprościć, ale o tym za chwilę.

Wzór i jego użycie

Wzór, którego potrzebujemy do obliczenia pola trójkąta równobocznego wpisanego w okrąg o promieniu R, wygląda następująco:

P = (3√3 / 4) * R²

Gdzie:

• P oznacza pole trójkąta równobocznego
• √3 to pierwiastek kwadratowy z 3 (w przybliżeniu 1.732)
• R to promień okręgu, w który wpisany jest trójkąt

Czyli, żeby obliczyć pole takiego trójkąta, wystarczy znać promień okręgu i wstawić go do tego wzoru. Pomnóż kwadrat promienia przez (3√3)/4 i gotowe!

Przykłady obliczeń

Żeby to lepiej zrozumieć, zobaczmy kilka przykładów:

Przykład 1:

Załóżmy, że promień okręgu, w który wpisany jest trójkąt równoboczny, wynosi 4 cm. Czyli R = 4. Wstawiamy to do wzoru:

P = (3√3 / 4) * 4² = (3√3 / 4) * 16 = 3√3 * 4 = 12√3 cm²

Czyli pole tego trójkąta wynosi 12√3 centymetrów kwadratowych, co w przybliżeniu daje około 20.78 cm².

Przykład 2:

Promień okręgu wynosi 5 metrów. R = 5.

P = (3√3 / 4) * 5² = (3√3 / 4) * 25 = (75√3) / 4 m²

Pole tego trójkąta to (75√3) / 4 metrów kwadratowych, czyli w przybliżeniu 32.48 m².

Przykład 3:

Promień okręgu wynosi 2 jednostki (np. decymetry). R = 2.

P = (3√3 / 4) * 2² = (3√3 / 4) * 4 = 3√3 dm²

Pole tego trójkąta to 3√3 decymetrów kwadratowych, czyli w przybliżeniu 5.20 dm².

Jak zapamiętać wzór?

Wzór P = (3√3 / 4) * R² może wydawać się skomplikowany, ale da się go zapamiętać. Pomyśl o tym tak: masz promień do kwadratu (R²), który jest mnożony przez pewną stałą. Ta stała to (3√3) / 4. Spróbuj zapamiętać, że w liczniku masz 3 razy pierwiastek z 3, a w mianowniku 4. Z czasem wejdzie Ci to w krew.

Alternatywne metody (bez wdawania się w szczegóły)

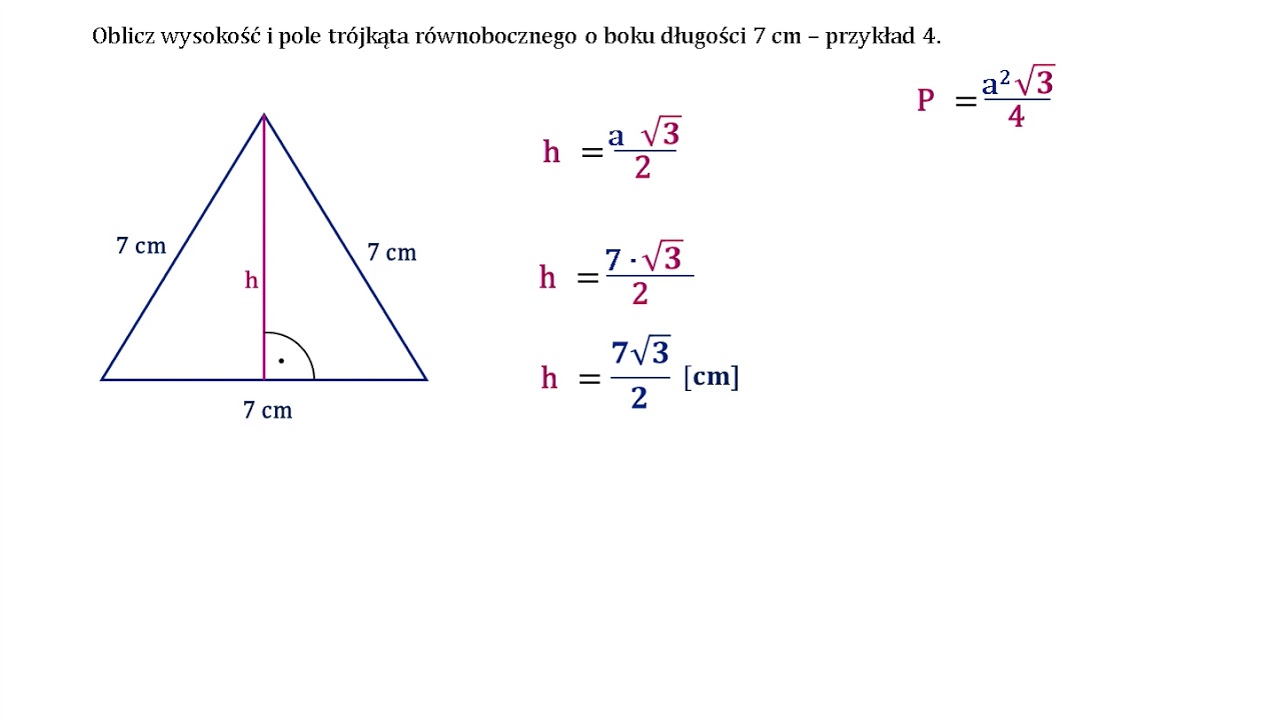
Chociaż wzór P = (3√3 / 4) * R² jest najprostszy do bezpośredniego obliczenia pola, można dojść do niego również innymi drogami. Na przykład, można obliczyć długość boku trójkąta równobocznego (a) na podstawie promienia okręgu, używając zależności: a = R√3. A następnie, mając długość boku, można obliczyć pole ze wzoru na pole trójkąta równobocznego: P = (a²√3) / 4. Ale to już wymaga więcej kroków i obliczeń, więc wygodniej jest pamiętać pierwszy wzór.

Podsumowanie

Pamiętaj, że kluczem do sukcesu jest zrozumienie, co oznaczają poszczególne elementy we wzorze i regularne ćwiczenia. Spróbuj rozwiązać kilka zadań z różnymi wartościami promienia, żeby nabrać wprawy. Możesz też poszukać w Internecie kalkulatorów, które obliczają pole trójkąta równobocznego wpisanego w okrąg, żeby sprawdzić swoje wyniki.

Mam nadzieję, że to wyjaśnienie było dla Ciebie pomocne! Powodzenia w rozwiązywaniu zadań!