Wzor Na Pole Trojkata Prostokatnego Wpisanego W Okrag

Dzień dobry wszystkim! Często dostaję od Was pytania dotyczące geometrii, a szczególnie pola trójkąta prostokątnego wpisanego w okrąg. Postaram się to wyjaśnić w prosty i zrozumiały sposób.

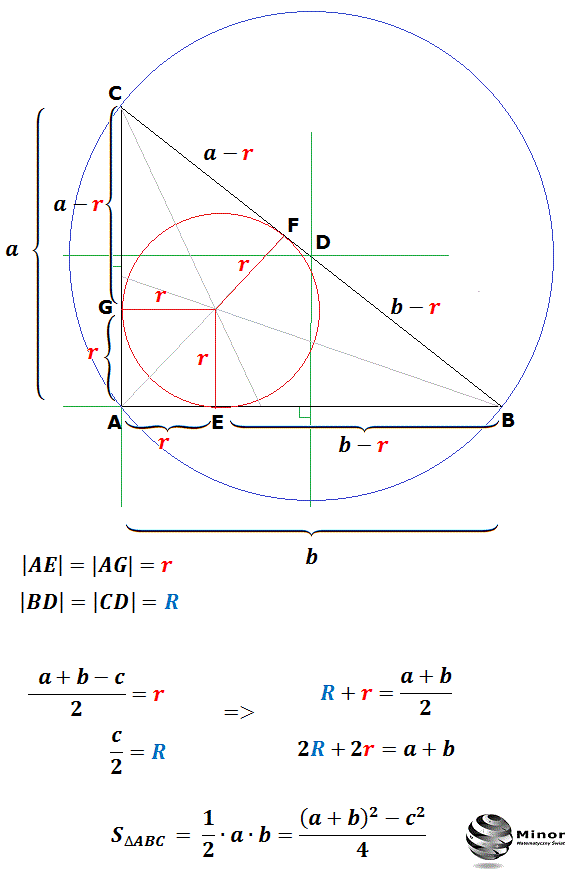
Zacznijmy od podstaw. Co to znaczy, że trójkąt jest wpisany w okrąg? Oznacza to, że wszystkie trzy wierzchołki trójkąta leżą na okręgu. Teraz, skupmy się na trójkącie prostokątnym. Ma on jeden kąt prosty (90 stopni). I tutaj pojawia się kluczowa informacja – jeśli trójkąt prostokątny jest wpisany w okrąg, to jego przeciwprostokątna (najdłuższy bok, leżący naprzeciw kąta prostego) jest jednocześnie średnicą tego okręgu. To bardzo ważny fakt, który upraszcza wiele obliczeń.

Jak zatem obliczyć pole takiego trójkąta? Przypomnijmy sobie wzór na pole dowolnego trójkąta:

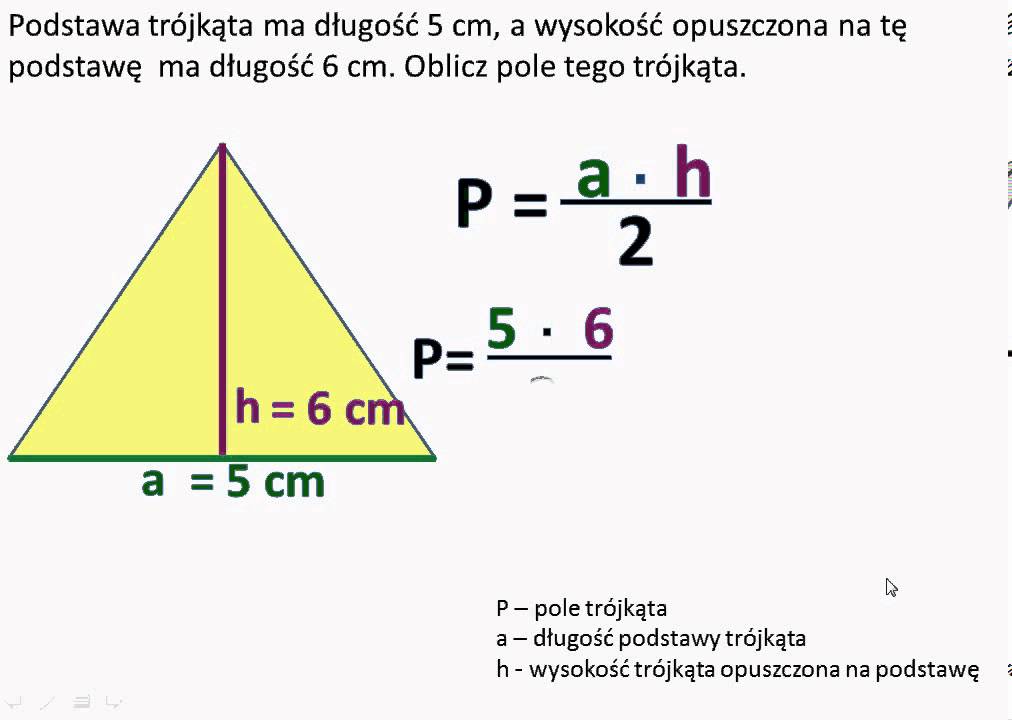
Pole = (1/2) * podstawa * wysokość

W przypadku trójkąta prostokątnego, sprawa jest prostsza, ponieważ jego przyprostokątne (boki tworzące kąt prosty) są jednocześnie podstawą i wysokością. Czyli:

Pole = (1/2) * a * b

gdzie 'a' i 'b' to długości przyprostokątnych.

Problem pojawia się, gdy nie znamy bezpośrednio długości przyprostokątnych, a np. znamy promień okręgu, w który trójkąt jest wpisany i długość jednej z przyprostokątnych. Wtedy musimy wykorzystać twierdzenie Pitagorasa i fakt, że przeciwprostokątna jest średnicą okręgu.

Załóżmy, że znamy promień okręgu 'r' i długość jednej z przyprostokątnych 'a'. Wiemy, że średnica okręgu, czyli przeciwprostokątna trójkąta, ma długość 2r. Z twierdzenia Pitagorasa:

a² + b² = (2r)²

Możemy wyliczyć długość drugiej przyprostokątnej 'b':

b² = (2r)² - a² b = √(4r² - a²)

Teraz, gdy znamy 'a' i 'b', możemy obliczyć pole trójkąta:

Pole = (1/2) * a * √(4r² - a²)

Rozważmy konkretny przykład. Załóżmy, że promień okręgu wynosi 5 cm, a jedna z przyprostokątnych ma długość 6 cm. Obliczmy długość drugiej przyprostokątnej:

b = √(4 * 5² - 6²) b = √(100 - 36) b = √64 b = 8 cm

Teraz obliczamy pole trójkąta:

Pole = (1/2) * 6 cm * 8 cm Pole = 24 cm²

Inny przykład: załóżmy, że znamy tylko promień okręgu, np. r = 4. Niech jedna z przyprostokątnych będzie miała długość a = 2. Wtedy:

b = √(4 * 4² - 2²) = √(64 - 4) = √60 = 2√15

Pole = (1/2) * 2 * 2√15 = 2√15

Wzory i Przykłady

Podsumujmy, najważniejsze wzory, które musicie zapamiętać:

• Pole trójkąta prostokątnego: P = (1/2) * a * b (gdzie a i b to przyprostokątne)
• Twierdzenie Pitagorasa: a² + b² = c² (gdzie c to przeciwprostokątna)
• Przeciwprostokątna trójkąta prostokątnego wpisanego w okrąg jest średnicą okręgu: c = 2r (gdzie r to promień okręgu)

Wykorzystując te wzory, możemy rozwiązać wiele zadań związanych z trójkątami prostokątnymi wpisanymi w okrąg. Pamiętajcie, żeby zawsze zaczynać od narysowania rysunku poglądowego, to bardzo pomaga w zrozumieniu zadania.

Zadania i ich Rozwiązania

Spróbujmy rozwiązać kilka dodatkowych zadań.

Zadanie 1: Trójkąt prostokątny jest wpisany w okrąg o promieniu 10 cm. Jedna z przyprostokątnych ma długość 12 cm. Oblicz pole trójkąta.

Rozwiązanie:

1. Przeciwprostokątna (średnica okręgu) ma długość 2 * 10 cm = 20 cm.
2. Korzystamy z twierdzenia Pitagorasa: 12² + b² = 20²
3. 144 + b² = 400
4. b² = 400 - 144 = 256
5. b = √256 = 16 cm
6. Pole = (1/2) * 12 cm * 16 cm = 96 cm²

Zadanie 2: Pole trójkąta prostokątnego wpisanego w okrąg wynosi 24 cm². Przeciwprostokątna ma długość 10 cm. Oblicz długości przyprostokątnych.

Rozwiązanie:

1. Wiemy, że c = 10 cm, więc a² + b² = 10² = 100
2. Wiemy, że (1/2) * a * b = 24, więc a * b = 48
3. Musimy rozwiązać układ równań:
   • a² + b² = 100
   • a * b = 48
4. Z drugiego równania wyznaczamy a = 48/b i podstawiamy do pierwszego równania:
   • (48/b)² + b² = 100
   • 2304/b² + b² = 100
   • 2304 + b⁴ = 100b²
   • b⁴ - 100b² + 2304 = 0
5. Wprowadzamy zmienną pomocniczą x = b²
   • x² - 100x + 2304 = 0
6. Rozwiązujemy równanie kwadratowe: Δ = (-100)² - 4 * 1 * 2304 = 10000 - 9216 = 784
   • √Δ = 28
   • x₁ = (100 + 28) / 2 = 64
   • x₂ = (100 - 28) / 2 = 36
7. Zatem:
   • b₁ = √64 = 8
   • b₂ = √36 = 6
8. Jeśli b = 8, to a = 48/8 = 6
9. Jeśli b = 6, to a = 48/6 = 8

Odp: Przyprostokątne mają długości 6 cm i 8 cm.

Zadanie 3: Oblicz pole trójkąta prostokątnego wpisanego w okrąg o promieniu 2√5, wiedząc że jedna z przyprostokątnych ma długość 4.

Rozwiązanie:

1. Przeciwprostokątna ma długość 2 * 2√5 = 4√5.
2. Korzystamy z twierdzenia Pitagorasa: 4² + b² = (4√5)²
3. 16 + b² = 16 * 5 = 80
4. b² = 80 - 16 = 64
5. b = √64 = 8
6. Pole = (1/2) * 4 * 8 = 16

Mam nadzieję, że te przykłady pomogą Wam lepiej zrozumieć, jak obliczać pole trójkąta prostokątnego wpisanego w okrąg. Pamiętajcie, że kluczem do sukcesu jest zrozumienie zależności między elementami trójkąta i okręgu oraz umiejętność wykorzystania wzorów. Powodzenia!