Wzór Na Pole Trójkat Równoramienny

Czy kiedykolwiek zastanawiałeś się, jak szybko i sprawnie obliczyć pole trójkąta równoramiennego? Może potrzebujesz tego do zadania szkolnego, projektu architektonicznego, a może po prostu z ciekawości. Niezależnie od powodu, ten artykuł jest dla Ciebie. Zrozumiemy, dlaczego wzór na pole trójkąta równoramiennego jest tak skonstruowany, a także nauczymy się go efektywnie wykorzystywać. Zapomnij o zawiłych obliczeniach – pokażemy Ci, jak to zrobić krok po kroku!

Czym Jest Trójkąt Równoramienny?

Zanim przejdziemy do wzoru, przypomnijmy sobie, co to właściwie jest trójkąt równoramienny. To trójkąt, który ma dwa boki o tej samej długości. Te boki nazywamy ramionami. Trzeci bok nazywamy podstawą. Kąty przy podstawie są równe. To ważna informacja, która będzie nam potrzebna później.

Wyobraź sobie trójkąt, w którym dwa boki mają po 5 cm, a podstawa ma 6 cm. To jest trójkąt równoramienny! Teraz spróbujmy zrozumieć, jak obliczyć jego pole.

Wzór na Pole Trójkąta Równoramiennego: Podstawa i Wysokość

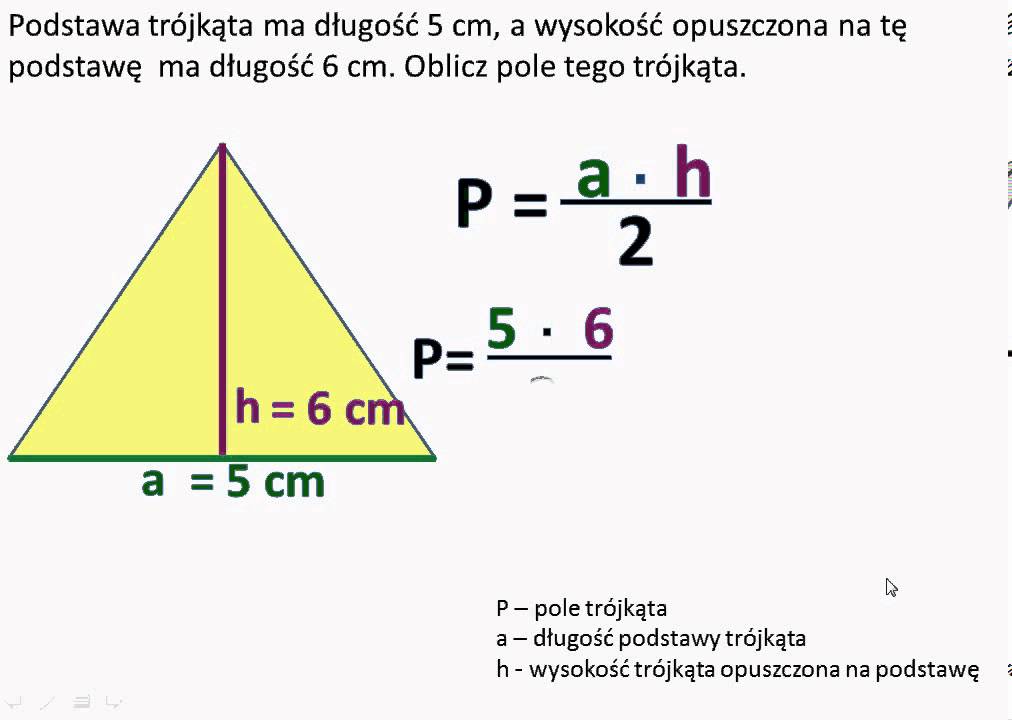
Najbardziej podstawowy i uniwersalny wzór na pole dowolnego trójkąta to:

Pole = (1/2) * podstawa * wysokość

W przypadku trójkąta równoramiennego również możemy go użyć. Ale pojawia się pytanie: skąd wziąć wysokość? Wysokość to odcinek poprowadzony z wierzchołka trójkąta prostopadle do podstawy. W trójkącie równoramiennym wysokość ta dzieli podstawę na dwie równe części. To bardzo przydatna właściwość!

Przykład: Mamy trójkąt równoramienny o podstawie 8 cm i wysokości 5 cm. Jego pole wynosi (1/2) * 8 cm * 5 cm = 20 cm². Proste, prawda?

Jak Obliczyć Wysokość? Twierdzenie Pitagorasa

Często zdarza się, że znamy długość ramion i podstawy, ale nie znamy wysokości. Wtedy z pomocą przychodzi twierdzenie Pitagorasa! Pamiętasz je? W trójkącie prostokątnym suma kwadratów długości przyprostokątnych (a i b) jest równa kwadratowi długości przeciwprostokątnej (c):

a² + b² = c²

W trójkącie równoramiennym wysokość dzieli go na dwa identyczne trójkąty prostokątne. Ramie trójkąta równoramiennego staje się przeciwprostokątną, połowa podstawy staje się jedną przyprostokątną, a wysokość staje się drugą przyprostokątną. Możemy więc zapisać:

(podstawa/2)² + wysokość² = ramię²

Przekształcając ten wzór, otrzymujemy:

wysokość² = ramię² - (podstawa/2)²

I w końcu:

wysokość = √(ramię² - (podstawa/2)²)

Przykład: Mamy trójkąt równoramienny, którego ramiona mają po 5 cm, a podstawa ma 6 cm. Obliczamy wysokość: wysokość = √(5² - (6/2)²) = √(25 - 9) = √16 = 4 cm. Teraz możemy obliczyć pole: Pole = (1/2) * 6 cm * 4 cm = 12 cm².

Wzór Herona dla Trójkąta Równoramiennego

Jeśli znasz długości wszystkich trzech boków trójkąta (w tym przypadku dwóch ramion i podstawy), możesz użyć wzoru Herona. Wzór ten jest bardziej ogólny i można go stosować do dowolnego trójkąta, niezależnie od jego kształtu.

Najpierw obliczamy połowę obwodu, oznaczaną literą *p*:

p = (a + b + c) / 2

Gdzie a, b i c to długości boków trójkąta. W przypadku trójkąta równoramiennego a = b (ramiona) i c = podstawa.

Następnie obliczamy pole ze wzoru:

Pole = √(p * (p - a) * (p - b) * (p - c))

Przykład: Mamy trójkąt równoramienny, którego ramiona mają po 5 cm, a podstawa ma 6 cm. Obliczamy połowę obwodu: p = (5 + 5 + 6) / 2 = 8 cm. Następnie obliczamy pole: Pole = √(8 * (8 - 5) * (8 - 5) * (8 - 6)) = √(8 * 3 * 3 * 2) = √144 = 12 cm².

Widzisz? Otrzymaliśmy ten sam wynik, co poprzednio, ale używając innego wzoru!

Wzór z Użyciem Kąta Między Ramionami

Czasami zamiast wysokości, znamy kąt α (alfa) między ramionami trójkąta równoramiennego. Wtedy możemy skorzystać z następującego wzoru:

Pole = (1/2) * ramię * ramię * sin(α)

Pole = (1/2) * ramię² * sin(α)

Pamiętaj, że kąt α musi być wyrażony w radianach, jeśli używasz kalkulatora. W wielu przypadkach kąt jest podawany w stopniach, więc trzeba go przeliczyć na radiany. 180 stopni to π radianów (ok. 3.14159).

Przykład: Mamy trójkąt równoramienny, którego ramiona mają po 5 cm, a kąt między ramionami wynosi 30 stopni. Zamieniamy kąt na radiany: 30 stopni * (π / 180) = π/6 radianów. Obliczamy pole: Pole = (1/2) * 5² * sin(π/6) = (1/2) * 25 * 0.5 = 6.25 cm².

Podsumowanie: Wybierz Wzór, Który Najbardziej Ci Odpowiada

Obliczanie pola trójkąta równoramiennego może wydawać się skomplikowane, ale tak naprawdę mamy do dyspozycji kilka prostych i skutecznych wzorów:

(1/2) * podstawa * wysokość: Najbardziej podstawowy wzór, wymaga znajomości podstawy i wysokości.
Wysokość = √(ramię² - (podstawa/2)²): Pozwala obliczyć wysokość, jeśli znamy długość ramion i podstawy.
Wzór Herona: Użyteczny, gdy znamy długości wszystkich trzech boków.
(1/2) * ramię² * sin(α): Przydatny, gdy znamy długość ramion i kąt między nimi.

Wybierz ten wzór, który jest najbardziej odpowiedni dla danych, które posiadasz. Pamiętaj o jednostkach – zawsze wyrażaj pole w jednostkach kwadratowych (np. cm², m²).

Praktyczne Zastosowania Wiedzy o Polu Trójkąta Równoramiennego

Wiedza o tym, jak obliczyć pole trójkąta równoramiennego, przydaje się w wielu sytuacjach. Oto kilka przykładów:

Architektura i Budownictwo: Obliczanie powierzchni dachów, elewacji i innych elementów konstrukcyjnych.
Geodezja: Wyznaczanie powierzchni działek o nieregularnych kształtach.
Stolarstwo: Projektowanie i wykonywanie mebli o trójkątnych elementach.
Projektowanie Graficzne: Tworzenie logo i innych elementów wizualnych.
Matematyka i Fizyka: Rozwiązywanie problemów związanych z geometrią i trygonometrią.
Codzienne Życie: Obliczanie ilości materiału potrzebnego do uszycia flagi, żagla lub innego elementu o trójkątnym kształcie.

Pamiętaj: zrozumienie wzorów to podstawa, ale praktyka czyni mistrza! Spróbuj rozwiązać kilka zadań samodzielnie, a zobaczysz, że obliczanie pola trójkąta równoramiennego stanie się dla Ciebie proste i intuicyjne.

Mam nadzieję, że ten artykuł okazał się dla Ciebie pomocny i rozjaśnił wszelkie wątpliwości dotyczące wzoru na pole trójkąta równoramiennego. Powodzenia w obliczeniach!