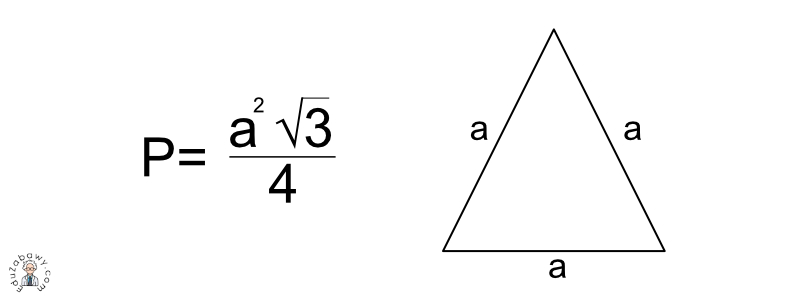Wzór Na Pole Trójkat Równoboczny

Czy kiedykolwiek zastanawiałeś się, jak szybko i sprawnie obliczyć pole trójkąta równobocznego? Jeśli tak, to świetnie trafiłeś! Ten artykuł jest skierowany do wszystkich, od uczniów szkół podstawowych po studentów, a nawet hobbystów, którzy chcą odświeżyć swoją wiedzę z geometrii. Naszym celem jest przedstawienie jasnego i zrozumiałego wyjaśnienia wzoru na pole trójkąta równobocznego, wraz z praktycznymi przykładami, które pomogą Ci go zapamiętać i stosować.

Czym jest Trójkąt Równoboczny?

Zanim przejdziemy do samego wzoru, upewnijmy się, że rozumiemy, czym jest trójkąt równoboczny. To specjalny rodzaj trójkąta, który charakteryzuje się tym, że wszystkie trzy boki mają jednakową długość, a wszystkie trzy kąty są równe 60 stopni. To sprawia, że trójkąt równoboczny jest bardzo regularną i symetryczną figurą geometryczną.

Dlaczego Trójkąty Równoboczne Są Ważne?

Trójkąty równoboczne pojawiają się w wielu dziedzinach życia. Od konstrukcji budynków i mostów (gdzie ich stabilność jest bardzo cenna), po projekty graficzne i sztukę (gdzie wykorzystuje się ich estetyczny wygląd), znajomość ich właściwości jest niezwykle przydatna. Pomijając aspekty praktyczne, rozumienie geometrii trójkątów równobocznych rozwija nasze myślenie przestrzenne i logiczne, co przydaje się w wielu innych dziedzinach życia.

Wzór na Pole Trójkąta Równobocznego

Teraz przejdźmy do sedna sprawy: jak obliczyć pole trójkąta równobocznego. Wzór jest prosty i elegancki, a jego wyprowadzenie opiera się na kilku podstawowych zasadach geometrii. Pole trójkąta równobocznego o boku długości 'a' wyraża się wzorem:

P = (a² * √3) / 4

Gdzie:

• P oznacza pole trójkąta.
• a oznacza długość boku trójkąta.
• √3 oznacza pierwiastek kwadratowy z 3 (w przybliżeniu 1.732).

Jak widzisz, do obliczenia pola potrzebujesz tylko jednej informacji: długości boku trójkąta! To sprawia, że wzór jest bardzo łatwy w użyciu.

Skąd się bierze ten wzór?

Aby lepiej zrozumieć, skąd się bierze ten wzór, spójrzmy na jego wyprowadzenie. Możemy podzielić trójkąt równoboczny na dwa trójkąty prostokątne, rysując wysokość z jednego wierzchołka na przeciwległy bok. Wysokość ta dzieli podstawę na pół. Używając twierdzenia Pitagorasa, możemy obliczyć wysokość (h) trójkąta równobocznego o boku 'a':

a² = (a/2)² + h²

h² = a² - (a²/4)

h² = (3a²/4)

h = (a√3)/2

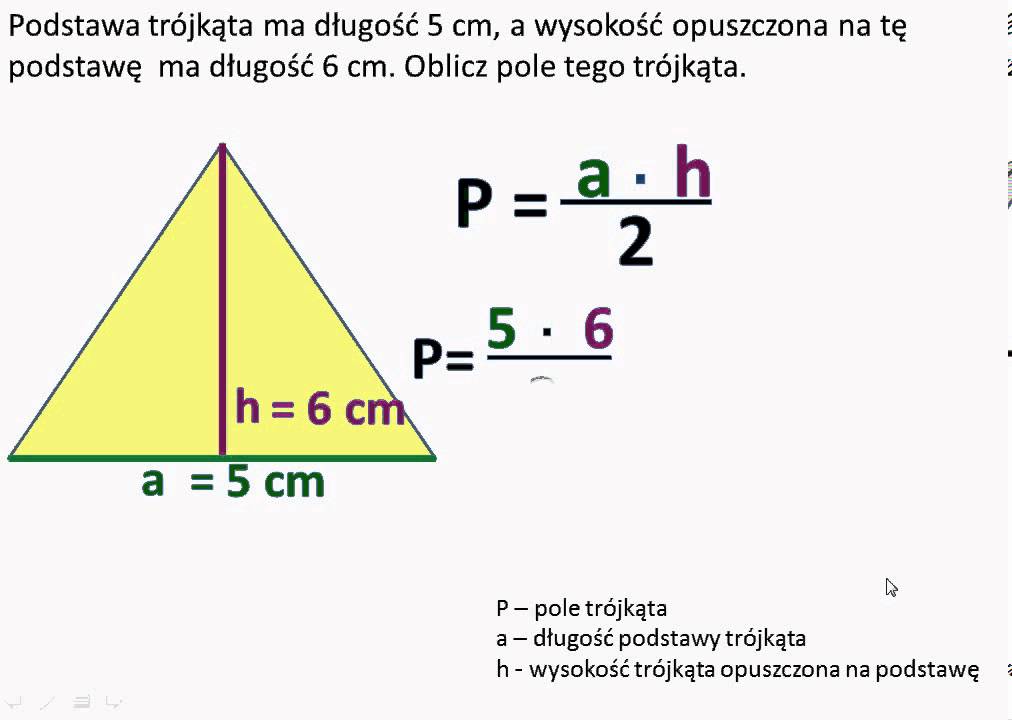
Następnie, używając ogólnego wzoru na pole trójkąta (P = 1/2 * podstawa * wysokość), otrzymujemy:

P = 1/2 * a * (a√3)/2

P = (a² * √3) / 4

Teraz widzisz, że wzór na pole trójkąta równobocznego jest bezpośrednią konsekwencją twierdzenia Pitagorasa i ogólnego wzoru na pole trójkąta.

Przykłady Obliczeń

Aby jeszcze lepiej zrozumieć, jak stosować ten wzór, przeanalizujmy kilka przykładów:

Przykład 1: Oblicz pole trójkąta równobocznego o boku długości 6 cm.

Rozwiązanie:

• a = 6 cm
• P = (a² * √3) / 4 = (6² * √3) / 4 = (36 * √3) / 4 = 9√3 cm²
• Przybliżona wartość: P ≈ 9 * 1.732 ≈ 15.588 cm²

Przykład 2: Oblicz pole trójkąta równobocznego o boku długości 10 m.

Rozwiązanie:

• a = 10 m
• P = (a² * √3) / 4 = (10² * √3) / 4 = (100 * √3) / 4 = 25√3 m²
• Przybliżona wartość: P ≈ 25 * 1.732 ≈ 43.3 m²

Przykład 3: Mamy trójkąt równoboczny o boku długości 4.5 jednostki. Oblicz jego pole.

Rozwiązanie:

• a = 4.5
• P = (a² * √3) / 4 = (4.5² * √3) / 4 = (20.25 * √3) / 4 = 5.0625√3 jednostek²
• Przybliżona wartość: P ≈ 5.0625 * 1.732 ≈ 8.77 jednostek²

Pamiętaj, że jednostka pola jest zawsze kwadratem jednostki długości boku.

Praktyczne Zastosowania

Gdzie w życiu codziennym możemy spotkać się z trójkątami równobocznymi i potrzebą obliczenia ich pola?

• Architektura i Budownictwo: Projektowanie dachów, elewacji budynków, mostów. Wyobraź sobie architekta projektującego dach o kształcie trójkąta równobocznego. Potrzebuje on obliczyć jego pole, aby oszacować ilość materiału potrzebnego do pokrycia dachu.
• Inżynieria: Obliczanie wytrzymałości konstrukcji opartych na trójkątach (np. kratownice). Inżynierowie często wykorzystują trójkąty w konstrukcjach, ponieważ są one bardzo stabilne. Znajomość pola trójkąta pozwala im obliczyć obciążenia, jakie może wytrzymać konstrukcja.
• Projektowanie Graficzne: Tworzenie logo, ikon, wzorów. Projektant graficzny może użyć trójkątów równobocznych do stworzenia logo firmy. Obliczenie pola trójkąta może pomóc mu w dopasowaniu rozmiaru logo do różnych nośników.
• Stolarstwo i Rzemiosło: Wycinanie elementów dekoracyjnych, tworzenie mozaik. Stolarz może wykorzystać trójkąty równoboczne do stworzenia dekoracyjnej mozaiki na drewnianej skrzynce. Obliczenie pola trójkąta pomoże mu w precyzyjnym wycięciu elementów.
• Geodezja i Kartografia: Wyznaczanie powierzchni działek o nieregularnych kształtach (przybliżanie ich do trójkątów). Geodeta może użyć trójkątów do przybliżonego obliczenia powierzchni działki o nieregularnym kształcie. Im więcej trójkątów, tym dokładniejsze przybliżenie.

Porady i Sztuczki

Oto kilka dodatkowych wskazówek, które mogą Ci się przydać:

• Zapamiętaj Wzór: Najlepszym sposobem na zapamiętanie wzoru jest regularne jego używanie. Rozwiązuj jak najwięcej zadań, a wzór sam wejdzie Ci do głowy.
• Sprawdzaj Jednostki: Upewnij się, że używasz spójnych jednostek. Jeśli bok jest podany w centymetrach, to pole będzie w centymetrach kwadratowych.
• Używaj Kalkulatora: Jeśli masz dostęp do kalkulatora, wykorzystaj go do obliczenia pierwiastka kwadratowego z 3. To znacznie przyspieszy obliczenia.
• Przybliżaj Wyniki: W praktycznych zastosowaniach często wystarczy przybliżona wartość pola. Zaokrąglij wynik do odpowiedniej liczby miejsc po przecinku.
• Ćwicz, Ćwicz, Ćwicz: Im więcej ćwiczysz, tym lepiej zrozumiesz wzór i nauczysz się go stosować w różnych sytuacjach.

Podsumowanie

W tym artykule omówiliśmy wzór na pole trójkąta równobocznego, pokazaliśmy, skąd się on bierze, i zaprezentowaliśmy kilka praktycznych przykładów jego zastosowania. Mamy nadzieję, że teraz z łatwością będziesz mógł obliczyć pole dowolnego trójkąta równobocznego!

Pamiętaj, że geometria to nie tylko wzory i definicje, ale przede wszystkim narzędzie do zrozumienia otaczającego nas świata. Im lepiej rozumiesz zasady geometrii, tym łatwiej będzie Ci rozwiązywać problemy i podejmować decyzje w życiu codziennym.

Dziękujemy za przeczytanie! Zachęcamy do dalszego zgłębiania wiedzy z zakresu matematyki i geometrii. Życzymy powodzenia w nauce i wielu sukcesów!