Wzór Na Pole Trójkat Prostokatny

W geometrii, trójkąt prostokątny zajmuje szczególne miejsce, zarówno ze względu na swoje unikalne właściwości, jak i szerokie zastosowanie w różnych dziedzinach. Obliczanie jego pola jest fundamentalną umiejętnością, a odpowiedni wzór jest stosunkowo prosty do zapamiętania i zastosowania. W tym artykule przyjrzymy się szczegółowo wzorowi na pole trójkąta prostokątnego, omówimy jego wyprowadzenie, wskażemy przykłady zastosowań i rozważymy jego znaczenie w kontekście praktycznym.

Podstawy Trójkąta Prostokątnego

Zanim przejdziemy do samego wzoru, warto przypomnieć sobie podstawowe cechy trójkąta prostokątnego. Jest to trójkąt, w którym jeden z kątów ma miarę 90 stopni, czyli jest kątem prostym. Bok leżący naprzeciw kąta prostego nazywamy przeciwprostokątną, a dwa pozostałe boki, które tworzą kąt prosty, nazywamy przyprostokątnymi.

Te przyprostokątne są kluczowe do obliczenia pola trójkąta prostokątnego, a długość każdego z nich będzie oznaczana zmiennymi. Przykładowo, jeden z nich nazwiemy 'a', a drugi 'b'.

Wzór na Pole Trójkąta Prostokątnego

Najprostszy i najbardziej popularny wzór na pole trójkąta prostokątnego to:

Pole = (1/2) * a * b

Gdzie:

• a i b to długości przyprostokątnych trójkąta.

Czyli pole trójkąta prostokątnego jest równe połowie iloczynu długości jego przyprostokątnych.

Wyprowadzenie Wzoru

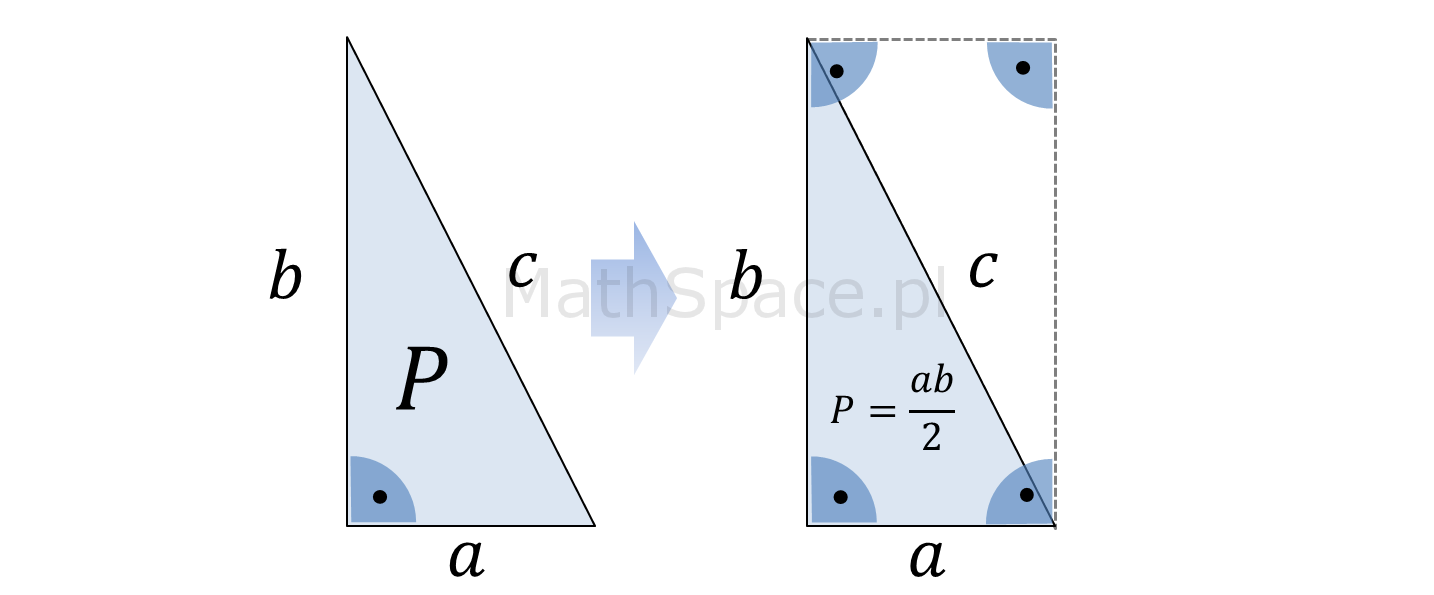
Wzór ten można łatwo wyprowadzić z bardziej ogólnego wzoru na pole trójkąta: Pole = (1/2) * podstawa * wysokość. W trójkącie prostokątnym, jeśli jedną z przyprostokątnych uznamy za podstawę, to druga przyprostokątna staje się wysokością. Dzieje się tak, ponieważ przyprostokątne są do siebie prostopadłe (tworzą kąt prosty). W rezultacie, możemy po prostu zamienić "podstawa" i "wysokość" na 'a' i 'b', uzyskując wzór (1/2) * a * b.

Inny sposób myślenia o tym wzorze, to wyobrażenie sobie trójkąta prostokątnego jako połowy prostokąta. Prostokąt o bokach 'a' i 'b' ma pole równe a * b. Trójkąt prostokątny, który jest "odcięty" od tego prostokąta po jego przekątnej, ma pole równe połowie pola prostokąta. To wizualne podejście pomaga w zrozumieniu, dlaczego we wzorze pojawia się współczynnik (1/2).

Przykłady Zastosowania

Spójrzmy na kilka przykładów, aby lepiej zrozumieć, jak stosować ten wzór:

Przykład 1:

Trójkąt prostokątny ma przyprostokątne o długościach 5 cm i 8 cm. Oblicz jego pole.

Rozwiązanie:

Pole = (1/2) * 5 cm * 8 cm = (1/2) * 40 cm² = 20 cm²

Odpowiedź: Pole trójkąta wynosi 20 cm².

Przykład 2:

Dach budynku ma kształt trójkąta prostokątnego. Jedna przyprostokątna ma długość 4 metry, a druga 6 metrów. Ile metrów kwadratowych materiału potrzeba na pokrycie tego dachu?

Rozwiązanie:

Pole = (1/2) * 4 m * 6 m = (1/2) * 24 m² = 12 m²

Odpowiedź: Potrzeba 12 m² materiału.

Przykład 3:

Stolarz chce wyciąć trójkąt prostokątny z kawałka drewna. Chce, aby pole trójkąta wynosiło 15 cm², a jedna z przyprostokątnych miała długość 6 cm. Jaką długość musi mieć druga przyprostokątna?

Rozwiązanie:

15 cm² = (1/2) * 6 cm * b

15 cm² = 3 cm * b

b = 15 cm² / 3 cm = 5 cm

Odpowiedź: Druga przyprostokątna musi mieć długość 5 cm.

Zastosowania w Realnym Świecie

Wzór na pole trójkąta prostokątnego ma szerokie zastosowanie w wielu dziedzinach życia:

• Architektura i budownictwo: Obliczanie powierzchni dachów, ścian, czy podłóg o kształcie trójkątnym.
• Geodezja: Wyznaczanie powierzchni działek o nieregularnych kształtach, które można podzielić na trójkąty.
• Inżynieria: Projektowanie mostów, konstrukcji i innych elementów, w których występują elementy trójkątne.
• Grafika komputerowa i gry: Obliczanie powierzchni tekstur, modelowanie obiektów 3D.
• Nawigacja: Obliczanie odległości i kątów w triangulacji.

Przykładowo, w architekturze, przy projektowaniu dachu o kształcie trójkąta prostokątnego, znajomość jego pola jest niezbędna do oszacowania ilości materiału potrzebnego do jego pokrycia. To z kolei pozwala na dokładne oszacowanie kosztów i uniknięcie marnotrawstwa materiałów.

W geodezji, pomiary działek często wymagają podziału na mniejsze, łatwiejsze do obliczenia figury geometryczne, takie jak trójkąty. Znając współrzędne wierzchołków trójkąta, można obliczyć długości jego boków, a następnie, w przypadku trójkąta prostokątnego, jego pole.

Alternatywne Metody Obliczania Pola

Chociaż wzór (1/2) * a * b jest najprostszy w przypadku trójkąta prostokątnego, istnieją również inne metody obliczania pola trójkąta, które mogą być użyteczne w bardziej złożonych sytuacjach:

• Wzór Herona: Używany, gdy znamy długości wszystkich trzech boków trójkąta (a, b, c). Najpierw obliczamy połowę obwodu trójkąta: s = (a + b + c) / 2, a następnie stosujemy wzór: Pole = √(s(s-a)(s-b)(s-c)). Ten wzór jest uniwersalny, ale obliczeniowo bardziej złożony.
• Pole z użyciem sinusa kąta: Pole = (1/2) * a * b * sin(γ), gdzie 'a' i 'b' to długości dwóch boków, a 'γ' to kąt między nimi. W przypadku trójkąta prostokątnego, jeśli γ jest kątem prostym, to sin(γ) = 1, co upraszcza wzór do (1/2) * a * b.

Warto pamiętać o tych alternatywnych metodach, ponieważ mogą być one jedynym sposobem na obliczenie pola trójkąta, gdy nie znamy długości przyprostokątnych.

Znaczenie Dokładności Obliczeń

W praktyce, dokładność obliczeń pola trójkąta prostokątnego ma kluczowe znaczenie, szczególnie w zastosowaniach inżynieryjnych i budowlanych. Nawet niewielkie błędy w pomiarach długości boków mogą prowadzić do znaczących rozbieżności w obliczeniach powierzchni, co z kolei może skutkować problemami konstrukcyjnymi lub finansowymi. Dlatego też, należy zawsze dbać o precyzję pomiarów i stosować odpowiednie narzędzia pomiarowe.

Dodatkowo, ważne jest, aby pamiętać o jednostkach miary. Jeśli długości przyprostokątnych są podane w centymetrach, to pole będzie wyrażone w centymetrach kwadratowych. Podobnie, jeśli długości są podane w metrach, to pole będzie wyrażone w metrach kwadratowych. Zawsze należy upewnić się, że jednostki są spójne.

Podsumowanie

Wzór na pole trójkąta prostokątnego (Pole = (1/2) * a * b) jest jednym z podstawowych i najczęściej używanych wzorów w geometrii. Jego prostota i łatwość zastosowania sprawiają, że jest on niezwykle przydatny w wielu dziedzinach, od architektury i budownictwa po geodezję i grafikę komputerową. Zrozumienie wyprowadzenia tego wzoru oraz jego praktycznych zastosowań pozwala na skuteczne rozwiązywanie problemów związanych z obliczaniem powierzchni w różnych kontekstach.

Pamiętajmy, że umiejętność obliczania pola trójkąta prostokątnego to cenna umiejętność, która może przydać się w wielu sytuacjach życiowych i zawodowych. Dlatego warto ją doskonalić i stosować w praktyce.

Zachęcamy do dalszego zgłębiania wiedzy z zakresu geometrii i matematyki! Wykorzystuj zdobytą wiedzę w codziennych sytuacjach i obserwuj, jak geometria otacza nas z każdej strony.