Wzór Na Pole Rombu Z Sinusem

Czy kiedykolwiek zastanawiałeś się, jak w prosty i elegancki sposób obliczyć pole rombu, znając tylko długość jego boku i kąt ostry? A może po prostu potrzebujesz odświeżyć swoją wiedzę z geometrii? Ten artykuł jest dla Ciebie! Skierowany jest do uczniów szkół średnich, studentów, a także wszystkich entuzjastów matematyki, którzy chcą zrozumieć wzór na pole rombu z sinusem i nauczyć się go efektywnie stosować. Przygotuj się na matematyczną podróż, która rozjaśni Ci ten fascynujący temat!

Czym właściwie jest romb?

Zanim przejdziemy do wzoru, upewnijmy się, że rozumiemy, czym jest romb. Romb to równoległobok, który posiada wszystkie boki równej długości. Oznacza to, że ma on wiele cech wspólnych z kwadratem, ale nie musi mieć kątów prostych. Kluczowe cechy rombu to:

• Cztery boki równej długości.
• Przeciwległe kąty są równe.
• Przekątne przecinają się pod kątem prostym i dzielą na połowy.
• Przeciwległe boki są równoległe.

Wzory na pole rombu - przypomnienie

Istnieje kilka sposobów na obliczenie pola rombu. Przypomnijmy sobie te najpopularniejsze:

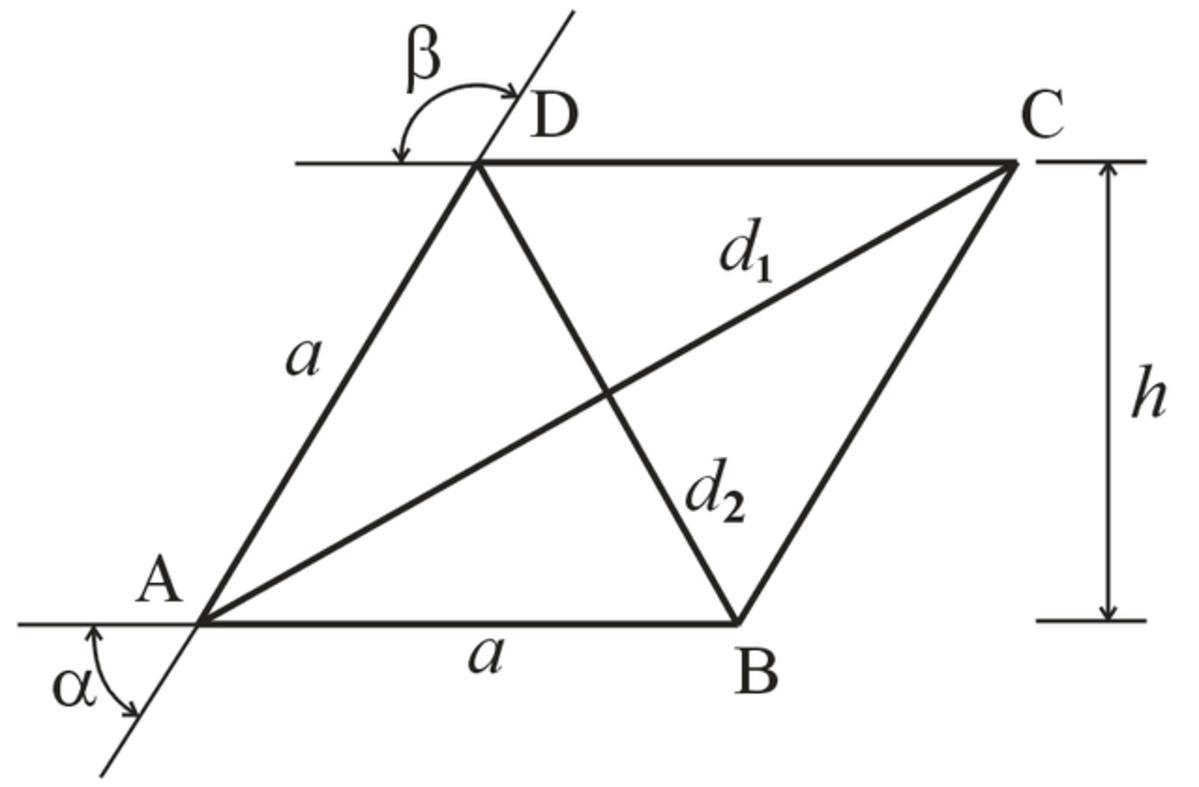
• Wzór z wykorzystaniem przekątnych: Pole rombu jest równe połowie iloczynu długości jego przekątnych (d₁ i d₂): P = (d₁ * d₂) / 2
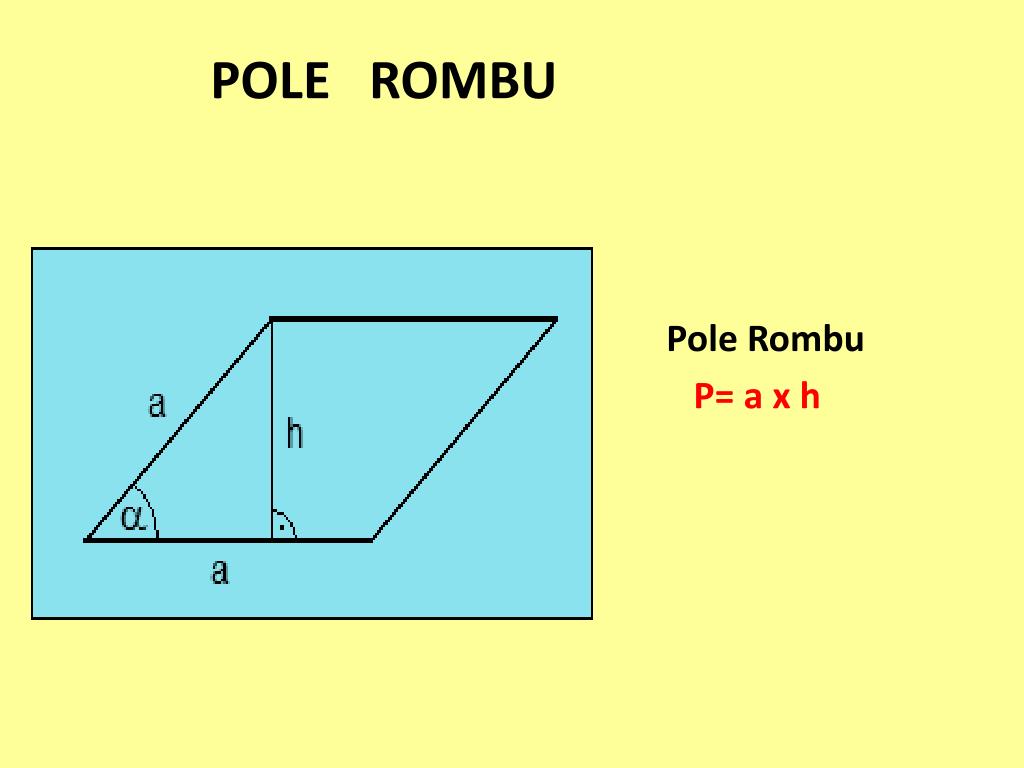
• Wzór z wykorzystaniem podstawy i wysokości: Pole rombu jest równe iloczynowi długości jego podstawy (a) i wysokości (h): P = a * h

Jednak co zrobić, gdy nie znamy długości przekątnych ani wysokości, ale znamy długość boku i jeden z kątów rombu? Wtedy na ratunek przychodzi wzór z sinusem!

Wzór na pole rombu z sinusem - sedno sprawy!

Wzór na pole rombu z sinusem jest niezwykle przydatny w sytuacjach, gdy znamy długość boku (a) rombu oraz miarę jednego z jego kątów, na przykład kąta ostrego (α). Wzór ten wygląda następująco:

P = a² * sin(α)

Gdzie:

• P - pole rombu
• a - długość boku rombu
• α - miara kąta ostrego rombu (lub kąta rozwartego; sinus kąta rozwartego jest równy sinusowi jego kąta przyległego ostrego).

Dlaczego to działa?

Wyobraźmy sobie, że romb jest "ściśniętym" prostokątem. Możemy wyprowadzić ten wzór, korzystając z podstawowego wzoru na pole równoległoboku (P = a * h) i trygonometrii. Wysokość (h) rombu, opuszczona na bok (a), tworzy z tym bokiem trójkąt prostokątny. Z definicji funkcji sinus w trójkącie prostokątnym mamy:

sin(α) = h / a

Stąd: h = a * sin(α)

Podstawiając to do wzoru na pole równoległoboku (P = a * h), otrzymujemy:

P = a * (a * sin(α)) = a² * sin(α)

Q.E.D.

Przykłady użycia wzoru z sinusem

Czas na praktykę! Zobaczmy, jak ten wzór sprawdza się w działaniu. Rozwiążmy kilka przykładów:

Przykład 1:

Romb ma bok długości 5 cm, a jego kąt ostry ma miarę 30°. Oblicz pole rombu.

Rozwiązanie:

a = 5 cm

α = 30°

sin(30°) = 0,5

P = a² * sin(α) = 5² * 0,5 = 25 * 0,5 = 12,5 cm²

Odpowiedź: Pole rombu wynosi 12,5 cm².

Przykład 2:

Oblicz pole rombu, którego bok ma długość 8 cm, a kąt rozwarty ma miarę 120°.

Rozwiązanie:

a = 8 cm

α = 120°

Kąt ostry przyległy do kąta rozwartego ma miarę 180° - 120° = 60°.

sin(120°) = sin(60°) = √3 / 2 (około 0,866)

P = a² * sin(α) = 8² * (√3 / 2) = 64 * (√3 / 2) = 32√3 cm² (około 55,43 cm²)

Odpowiedź: Pole rombu wynosi 32√3 cm² (około 55,43 cm²).

Przykład 3:

Dana jest działka w kształcie rombu o boku długości 10 metrów. Kąt ostry działki wynosi 45°. Ile metrów kwadratowych powierzchni ma ta działka?

Rozwiązanie:

a = 10 m

α = 45°

sin(45°) = √2 / 2 (około 0,707)

P = a² * sin(α) = 10² * (√2 / 2) = 100 * (√2 / 2) = 50√2 m² (około 70,71 m²)

Odpowiedź: Działka ma powierzchnię 50√2 m² (około 70,71 m²).

Kiedy stosować wzór z sinusem?

Wzór na pole rombu z sinusem jest najbardziej użyteczny w sytuacjach, gdy:

• Znamy długość boku rombu.
• Znamy miarę jednego z kątów rombu (ostrego lub rozwartego).
• Nie znamy długości przekątnych ani wysokości rombu, lub ich obliczenie byłoby bardziej skomplikowane.

Wybór odpowiedniego wzoru zależy od danych, które posiadamy. Zawsze warto rozważyć, który wzór będzie najprostszy i najszybszy do zastosowania w danej sytuacji.

Praktyczne zastosowania

Obliczanie pola rombu może wydawać się abstrakcyjne, ale ma wiele praktycznych zastosowań w życiu codziennym i różnych dziedzinach, takich jak:

• Architektura: Projektowanie podłóg, elewacji, okien i innych elementów budynków.
• Inżynieria: Obliczanie powierzchni elementów konstrukcyjnych o kształcie rombu.
• Geodezja: Mierzenie powierzchni działek o kształcie zbliżonym do rombu.
• Rękodzieło: Projektowanie wzorów i ornamentów na tkaninach, płytkach ceramicznych, mozaikach itp.
• Gry komputerowe: Tworzenie geometrii obiektów w grach.

Podsumowanie

Wzór na pole rombu z sinusem to potężne narzędzie, które pozwala nam obliczyć pole tej figury, znając tylko długość boku i miarę jednego z kątów. Jego wyprowadzenie opiera się na podstawowych zasadach trygonometrii i zrozumieniu relacji między bokami i kątami w rombie. Mamy nadzieję, że ten artykuł pomógł Ci zrozumieć i opanować ten wzór, a przykłady pokazały, jak go efektywnie stosować. Pamiętaj, że regularna praktyka jest kluczem do sukcesu w matematyce! Teraz, gdy znasz ten wzór, możesz z powodzeniem rozwiązywać zadania i mierzyć się z różnymi problemami geometrycznymi.

Zatem, śmiało, wykorzystaj tę wiedzę w praktyce i zostań mistrzem rombów!