Wzór Na Pole Powierzchni Walca

Czy kiedykolwiek zastanawiałeś się, jak obliczyć, ile farby potrzebujesz do pomalowania zbiornika na wodę o kształcie walca? Albo ile blachy zużyjesz do wykonania puszki na twoje ulubione ogórki konserwowe? Odpowiedź tkwi w znajomości wzoru na pole powierzchni walca. Brzmi skomplikowanie? Spokojnie, ten artykuł rozwieje wszelkie wątpliwości i pokaże, jak to zrobić w prosty i przystępny sposób.

Wiele osób uważa matematykę za abstrakcyjną i oderwaną od rzeczywistości. Często słyszymy: "Kiedy ja to w życiu wykorzystam?". Jednak znajomość podstawowych wzorów, takich jak ten na pole powierzchni walca, otwiera drzwi do rozwiązywania praktycznych problemów. Zrozumienie tych zasad pozwala nam lepiej funkcjonować w otaczającym nas świecie, od prostych zadań w domu po bardziej złożone obliczenia w pracy.

Dlaczego pole powierzchni walca jest ważne?

Zanim przejdziemy do samego wzoru, warto zrozumieć, dlaczego właściwie powinniśmy się nim interesować. Pole powierzchni walca ma zastosowanie w wielu dziedzinach życia, m.in.:

Budownictwo: Obliczanie ilości materiałów potrzebnych do wykonania elementów konstrukcyjnych, takich jak rury, kolumny, czy zbiorniki.
Produkcja: Określanie zużycia materiałów do produkcji puszek, opakowań cylindrycznych, czy innych wyrobów.
Inżynieria: Projektowanie rurociągów, zbiorników ciśnieniowych i innych urządzeń o kształcie walca.
Logistyka: Optymalizacja wykorzystania przestrzeni w magazynach i transporcie poprzez obliczanie powierzchni zajmowanej przez walcowate obiekty.
Dom i ogród: Obliczanie ilości farby potrzebnej do pomalowania beczki, pojemnika na deszczówkę, czy innych przedmiotów.

Wyobraź sobie, że budujesz domek letniskowy i potrzebujesz pomalować rurę odprowadzającą wodę deszczową. Jeśli nie znasz wzoru na pole powierzchni walca, możesz kupić za dużo farby (i przepłacić) lub za mało (i musieć jechać ponownie do sklepu). Znajomość tego wzoru pozwala uniknąć takich problemów.

Wzór na pole powierzchni walca – krok po kroku

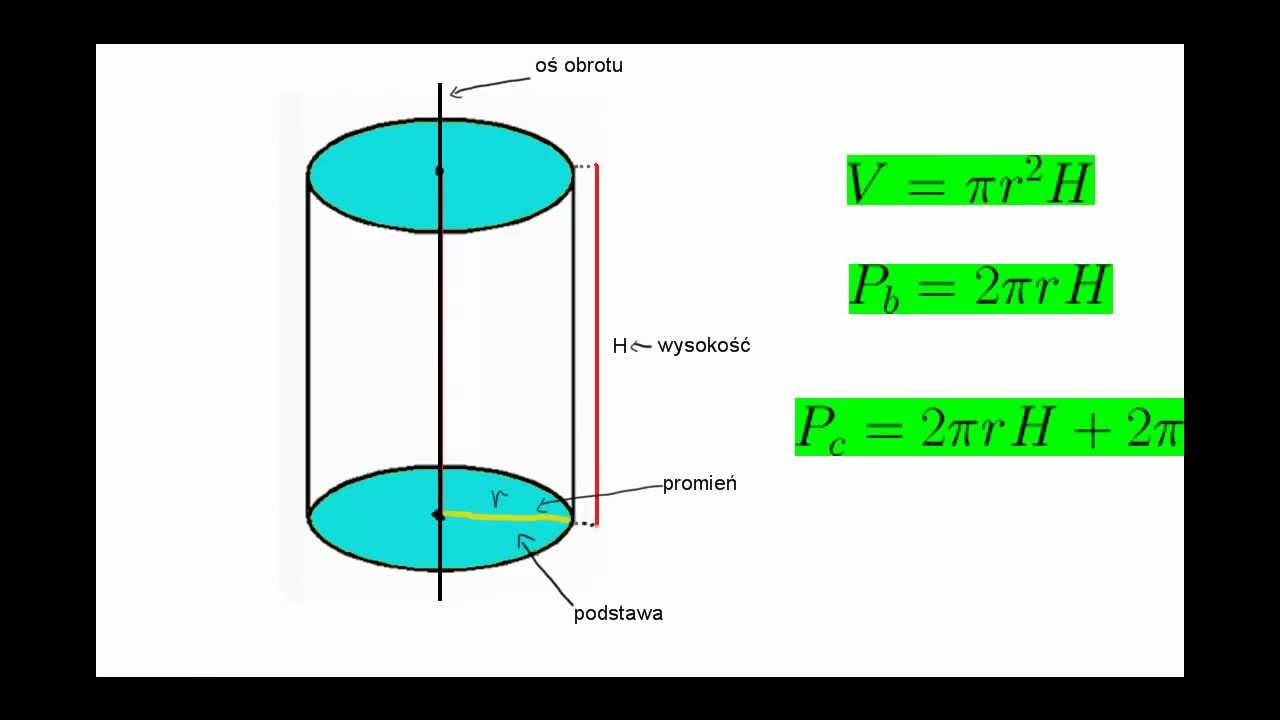
Wzór na pole powierzchni całkowitej walca (Pc) to:

Pc = 2πr² + 2πrh

Gdzie:

r – promień podstawy walca
h – wysokość walca
π (pi) – stała matematyczna, w przybliżeniu równa 3,14159

Ten wzór składa się z dwóch części:

2πr² – to pole powierzchni dwóch podstaw walca (dwóch kół). Każde koło ma pole πr², a ponieważ mamy dwa koła (podstawa górna i dolna), mnożymy to przez 2.
2πrh – to pole powierzchni bocznej walca. Wyobraź sobie, że rozwijasz powierzchnię boczną walca – otrzymasz prostokąt. Jeden bok tego prostokąta to obwód podstawy (2πr), a drugi bok to wysokość walca (h). Pole prostokąta to iloczyn długości boków, czyli 2πrh.

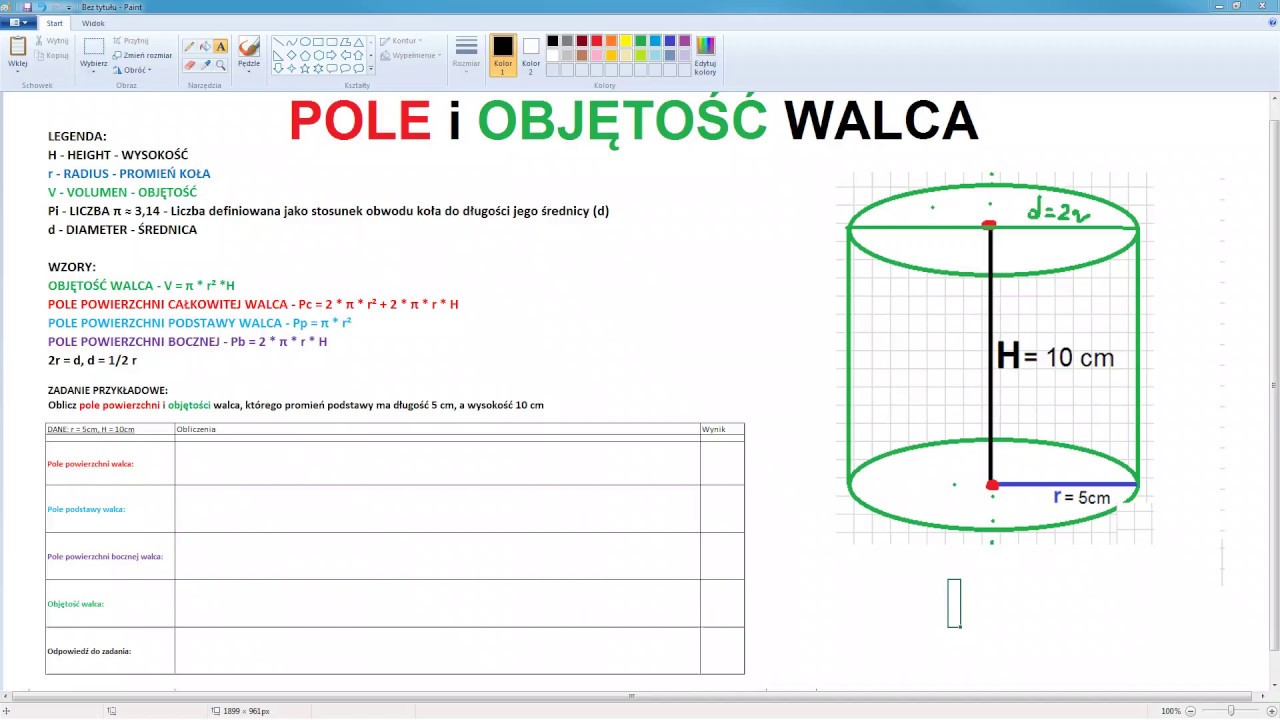
Przykład: Załóżmy, że mamy walec o promieniu podstawy r = 5 cm i wysokości h = 10 cm. Obliczmy jego pole powierzchni całkowitej.

Pc = 2πr² + 2πrh = 2 * 3,14159 * (5 cm)² + 2 * 3,14159 * 5 cm * 10 cm ≈ 157,08 cm² + 314,16 cm² ≈ 471,24 cm²

Zatem pole powierzchni całkowitej tego walca wynosi około 471,24 cm².

Pole powierzchni bocznej walca

Czasami potrzebujemy obliczyć tylko pole powierzchni bocznej walca, bez uwzględniania podstaw. Wtedy korzystamy z następującego wzoru:

Pb = 2πrh

Czyli, jak już wcześniej wspomniano, to po prostu obwód podstawy pomnożony przez wysokość walca.

Pole podstawy walca

Pole jednej podstawy walca, czyli koła, obliczamy za pomocą wzoru:

Pp = πr²

Potencjalne trudności i sposoby ich pokonania

Niektórzy mogą mieć trudności z zapamiętaniem wzoru. Istnieje kilka sposobów, aby ułatwić sobie to zadanie:

Zrozumienie skąd się bierze wzór: Jak wyjaśniono wcześniej, wzór na pole powierzchni całkowitej walca wynika z sumy pól dwóch podstaw (kół) i pola powierzchni bocznej (prostokąta). Zrozumienie tego faktu ułatwia zapamiętanie wzoru.
Ćwiczenia praktyczne: Im więcej przykładów rozwiążesz, tym lepiej utrwalisz wzór i zrozumiesz, jak go stosować w różnych sytuacjach.
Korzystanie z wizualizacji: Wyobraź sobie walec i rozwiń go na płasko. Zobaczysz wtedy dwa koła i prostokąt. To pomoże Ci zapamiętać, jakie elementy składają się na pole powierzchni całkowitej.
Wykorzystanie aplikacji i kalkulatorów online: Istnieje wiele narzędzi online, które mogą pomóc w obliczeniach i sprawdzeniu poprawności wyników.

Częstym błędem jest mylenie promienia (r) ze średnicą (d). Pamiętaj, że promień to połowa średnicy (r = d/2). Zawsze dokładnie sprawdzaj, jakie dane podane są w zadaniu.

Kontrargumenty i dlaczego wzór na pole powierzchni walca jest ważny

Niektórzy mogą argumentować, że w dzisiejszych czasach, kiedy mamy dostęp do kalkulatorów i komputerów, znajomość wzorów matematycznych nie jest już tak istotna. Można po prostu wpisać dane do kalkulatora i otrzymać wynik. Jest w tym trochę prawdy, ale znajomość wzoru pozwala na:

Zrozumienie problemu: Wpisanie danych do kalkulatora bez zrozumienia, co się dzieje, jest bezsensowne. Znajomość wzoru pozwala zrozumieć, jakie czynniki wpływają na pole powierzchni walca i jak je ze sobą powiązać.
Weryfikację wyników: Znając wzór, możemy oszacować wynik i sprawdzić, czy wynik otrzymany z kalkulatora jest w ogóle sensowny. Unikniemy w ten sposób błędów wynikających z nieprawidłowego wpisania danych.
Rozwiązywanie problemów w sytuacjach, gdy nie mamy dostępu do kalkulatora: Czasami możemy znaleźć się w sytuacji, gdy nie mamy dostępu do komputera lub kalkulatora. Wtedy znajomość wzoru pozwala na przybliżone obliczenia i rozwiązanie problemu.
Rozwój logicznego myślenia: Uczenie się matematyki, w tym wzorów, rozwija logiczne myślenie i umiejętność rozwiązywania problemów, które przydają się w wielu innych dziedzinach życia.

Podsumowując, znajomość wzoru na pole powierzchni walca to nie tylko umiejętność obliczania pola figury geometrycznej, ale także narzędzie, które pozwala na lepsze zrozumienie otaczającego nas świata i rozwiązywanie praktycznych problemów.

Podsumowanie i co dalej?

W tym artykule omówiliśmy wzór na pole powierzchni walca, wyjaśniliśmy, skąd się on bierze i pokazaliśmy, jak go stosować w praktyce. Dowiedzieliśmy się, dlaczego znajomość tego wzoru jest ważna i jakie korzyści z niej płyną. Pamiętaj, że kluczem do sukcesu jest praktyka – rozwiąż jak najwięcej zadań, a wzór na pole powierzchni walca stanie się dla Ciebie prosty i oczywisty.

Teraz, gdy znasz już wzór na pole powierzchni walca, spróbuj zastosować go w praktyce. Zmierz wymiary przedmiotów o kształcie walca w swoim otoczeniu (puszki, rury, kubki) i oblicz ich pole powierzchni. Możesz również poszukać zadań z geometrii w podręcznikach lub w Internecie i sprawdzić swoje umiejętności.

Czy widzisz już zastosowanie wzoru na pole powierzchni walca w swoim życiu? Jakie problemy możesz dzięki niemu rozwiązać?