Wzór Na Pole Powierzchni Rombu

Czy kiedykolwiek zastanawiałeś się, jak obliczyć, ile materiału potrzebujesz, aby pokryć dekoracyjny romb na ścianie? Albo jak precyzyjnie oszacować powierzchnię latawca w kształcie rombu, aby wiedzieć, ile farby na niego zużyć? Być może stoisz przed zadaniem związanym z projektem architektonicznym, gdzie romb jest kluczowym elementem wizualnym, a dokładne wyliczenia są niezbędne? Jeśli tak, to ten artykuł jest dla Ciebie.

Wiele osób ma trudności z zapamiętaniem i stosowaniem wzorów geometrycznych, zwłaszcza gdy chodzi o figury inne niż podstawowe kwadraty i prostokąty. Może to wynikać z braku praktycznego zastosowania w życiu codziennym lub po prostu z lęku przed matematyką. Ale nie martw się! Postaram się wyjaśnić wzór na pole powierzchni rombu w sposób prosty i zrozumiały, pokazując jego użyteczność w różnych sytuacjach.

W tym artykule skupimy się na tym, jak obliczyć pole powierzchni rombu. Zobaczymy, że w rzeczywistości jest to całkiem proste, jeśli zrozumiemy podstawowe zasady. Nie tylko podam wzór, ale także wyjaśnię, skąd się on bierze i jak go stosować w praktyce. Przyjrzymy się różnym metodom obliczeń, w zależności od danych, które posiadamy.

Dlaczego warto znać wzór na pole powierzchni rombu?

Zanim przejdziemy do samego wzoru, warto zastanowić się, dlaczego w ogóle powinniśmy się nim interesować. Otóż, wiedza ta przydaje się w wielu sytuacjach, zarówno w życiu codziennym, jak i w bardziej specjalistycznych dziedzinach:

• Dekoracja wnętrz: Obliczanie ilości tapety lub farby potrzebnej do pokrycia ściany z elementami romboidalnymi.
• Rękodzieło: Tworzenie mozaik, witraży czy innych projektów artystycznych, gdzie precyzyjne wyliczenia są kluczowe.
• Architektura i budownictwo: Projektowanie elewacji budynków, układanie płytek chodnikowych w kształcie rombów.
• Projektowanie gier: Tworzenie grafik i obiektów w grach komputerowych, gdzie romby mogą być użyte jako elementy terenu lub interfejsu.
• Matematyka i geometria: Rozwijanie umiejętności logicznego myślenia i rozwiązywania problemów geometrycznych.

Zatem, znajomość wzoru na pole rombu to nie tylko sucha wiedza teoretyczna, ale praktyczna umiejętność, która może przydać się w wielu różnych sytuacjach. A teraz, przejdźmy do konkretów!

Wzór na pole powierzchni rombu – podstawy

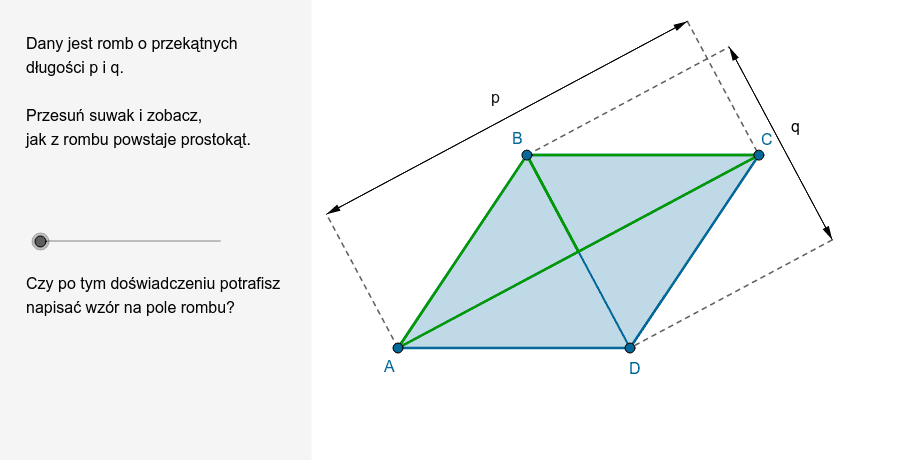
Najprostszy i najczęściej stosowany wzór na pole powierzchni rombu wykorzystuje długości jego przekątnych. Romb, jak wiemy, ma dwie przekątne, które przecinają się pod kątem prostym. Nazwijmy je d₁ i d₂. Wzór wygląda następująco:

Pole rombu (P) = (d₁ * d₂) / 2

Czyli, aby obliczyć pole powierzchni rombu, mnożymy długości jego przekątnych, a następnie dzielimy wynik przez 2. Proste, prawda?

Przykład: Załóżmy, że mamy romb, którego przekątne mają długość 6 cm i 8 cm. W takim przypadku pole powierzchni rombu wynosi:

P = (6 cm * 8 cm) / 2 = 48 cm² / 2 = 24 cm²

Zatem, pole powierzchni tego rombu to 24 centymetry kwadratowe.

Skąd się bierze ten wzór?

Można się zastanawiać, skąd właściwie wziął się ten wzór. Otóż, romb można podzielić na cztery identyczne trójkąty prostokątne, których przyprostokątne są połową długości przekątnych rombu. Pole każdego z tych trójkątów wynosi (1/2) * (d₁/2) * (d₂/2). Ponieważ mamy cztery takie trójkąty, mnożymy to przez 4, co daje nam:

4 * (1/2) * (d₁/2) * (d₂/2) = (d₁ * d₂) / 2

Innym sposobem na zrozumienie tego wzoru jest wyobrażenie sobie, że romb można przekształcić w prostokąt o bokach równych połowie długości przekątnych rombu. Przekształcenie to polega na przesunięciu dwóch trójkątów z rombu, tak aby utworzyły prostokąt. Wtedy pole tego prostokąta, a tym samym pole rombu, wynosi (d₁/2) * d₂ lub (d₂/2) * d₁, co jest równoważne (d₁ * d₂) / 2.

Alternatywne wzory na pole powierzchni rombu

Oprócz wzoru wykorzystującego przekątne, istnieją również inne sposoby obliczenia pola powierzchni rombu, w zależności od dostępnych danych:

1. Wzór wykorzystujący bok i wysokość

Jeśli znamy długość boku rombu (a) i wysokość opuszczoną na ten bok (h), możemy obliczyć pole powierzchni za pomocą wzoru:

Pole rombu (P) = a * h

Ten wzór jest analogiczny do wzoru na pole powierzchni równoległoboku, ponieważ romb jest szczególnym przypadkiem równoległoboku.

Przykład: Jeśli bok rombu ma długość 5 cm, a wysokość opuszczona na ten bok wynosi 4 cm, to pole powierzchni rombu wynosi:

P = 5 cm * 4 cm = 20 cm²

2. Wzór wykorzystujący bok i kąt

Jeśli znamy długość boku rombu (a) i miarę jednego z jego kątów (α), możemy obliczyć pole powierzchni za pomocą wzoru:

Pole rombu (P) = a² * sin(α)

Pamiętaj, że kąt α musi być wyrażony w stopniach lub radianach, w zależności od ustawień kalkulatora.

Przykład: Załóżmy, że bok rombu ma długość 7 cm, a jeden z jego kątów ma miarę 60 stopni. W takim przypadku pole powierzchni rombu wynosi:

P = 7² cm² * sin(60°) = 49 cm² * √3/2 ≈ 42.44 cm²

Kiedy używać którego wzoru?

Wybór odpowiedniego wzoru zależy od danych, które posiadamy. Jeśli znamy długości przekątnych, najłatwiej jest użyć wzoru P = (d₁ * d₂) / 2. Jeśli znamy długość boku i wysokość, używamy wzoru P = a * h. A jeśli znamy długość boku i kąt, używamy wzoru P = a² * sin(α).

Częste błędy i jak ich unikać

Podczas obliczania pola powierzchni rombu, często popełniane są następujące błędy:

• Pomylenie jednostek: Upewnij się, że wszystkie długości są wyrażone w tej samej jednostce (np. cm, m).
• Użycie nieodpowiedniego wzoru: Wybierz wzór, który pasuje do danych, które posiadasz.
• Błędy w obliczeniach: Sprawdź dokładnie swoje obliczenia, zwłaszcza jeśli używasz kalkulatora.
• Niewłaściwe użycie funkcji sinus: Upewnij się, że Twój kalkulator jest ustawiony na odpowiedni tryb (stopnie lub radiany).

Aby uniknąć tych błędów, zawsze sprawdzaj swoje obliczenia, upewnij się, że używasz odpowiednich jednostek i dokładnie przeczytaj treść zadania, aby zidentyfikować, jakie dane są Ci dostępne.

Podsumowanie i następne kroki

W tym artykule omówiliśmy wzór na pole powierzchni rombu i różne sposoby jego obliczania. Dowiedzieliśmy się, że:

• Najpopularniejszy wzór to: P = (d₁ * d₂) / 2, gdzie d₁ i d₂ to długości przekątnych.
• Można również użyć wzoru: P = a * h, gdzie a to długość boku, a h to wysokość.
• Lub wzoru: P = a² * sin(α), gdzie a to długość boku, a α to miara jednego z kątów.

Mam nadzieję, że teraz rozumiesz, jak obliczyć pole powierzchni rombu i potrafisz zastosować tę wiedzę w praktyce. Teraz, gdy już znasz wzór, zachęcam Cię do poćwiczenia na różnych przykładach. Spróbuj znaleźć w swoim otoczeniu przedmioty w kształcie rombu i oszacować ich powierzchnię. Możesz również spróbować rozwiązać różne zadania geometryczne związane z rombami.

Czy widzisz teraz, jak wiedza matematyczna może być przydatna w życiu codziennym? Jakie inne zagadnienia matematyczne chciałbyś/chciałabyś, abym omówił w przyszłości?