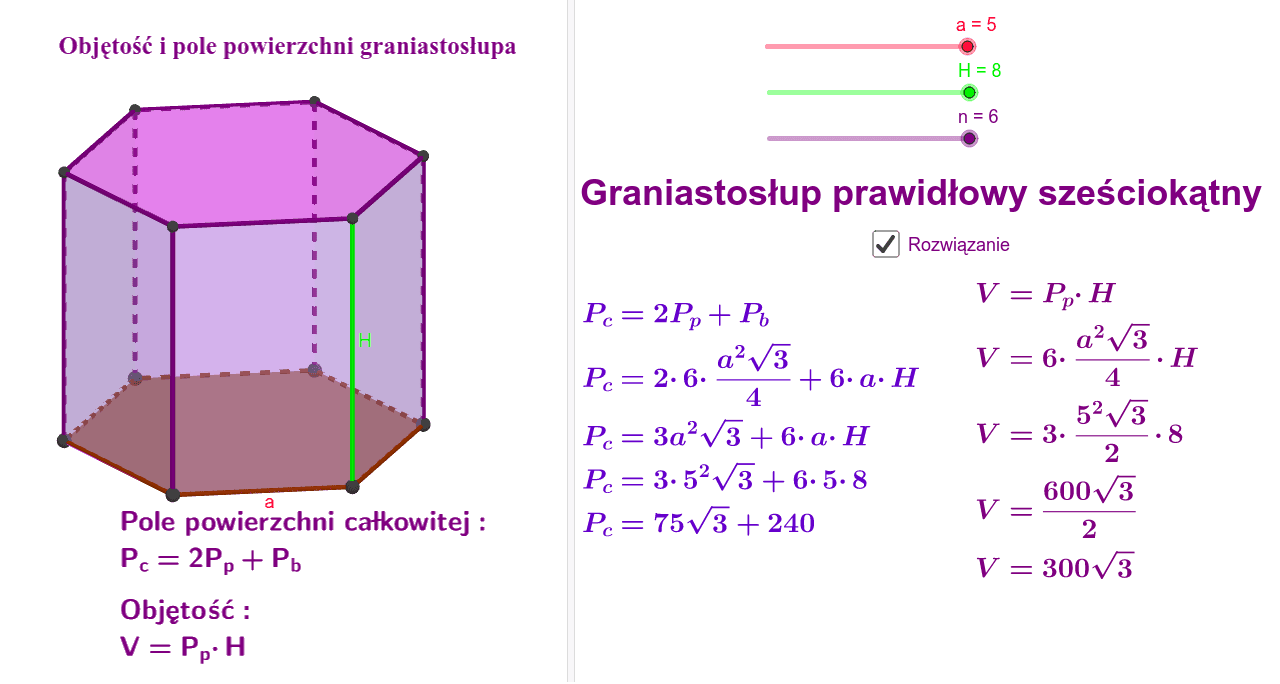
Wzór Na Pole Podstawy Graniastosłupa Prawidłowego Sześciokątnego

Graniastosłup prawidłowy sześciokątny to fascynująca figura geometryczna, której zrozumienie otwiera drzwi do bardziej zaawansowanych koncepcji matematycznych i inżynierskich. Centralnym elementem jego charakterystyki jest pole podstawy, które, jak się przekonamy, da się wyliczyć na kilka sposobów. Przyjrzyjmy się bliżej tej kwestii, analizując krok po kroku niezbędne obliczenia i wzory.

Podstawą graniastosłupa prawidłowego sześciokątnego jest, jak sama nazwa wskazuje, sześciokąt foremny. Sześciokąt foremny charakteryzuje się tym, że wszystkie jego boki mają równą długość, a wszystkie kąty wewnętrzne są równe. To sprawia, że jest on figurą wysoce symetryczną, co znacznie ułatwia obliczenia.

Najbardziej intuicyjnym sposobem na obliczenie pola sześciokąta foremnego jest podzielenie go na mniejsze, łatwiejsze do obliczenia figury. Możemy zauważyć, że sześciokąt foremny można podzielić na sześć identycznych trójkątów równobocznych, których wierzchołki spotykają się w środku sześciokąta. Pole każdego z tych trójkątów można obliczyć znając długość boku sześciokąta, która jest jednocześnie długością boku każdego z trójkątów równobocznych.

Wzór na pole trójkąta równobocznego o boku a wygląda następująco:

P = (a²√3) / 4

Skoro sześciokąt foremny składa się z sześciu takich trójkątów, to pole sześciokąta foremnego będzie równe sześciokrotności pola jednego trójkąta równobocznego. Zatem:

Pole sześciokąta = 6 * (a²√3) / 4

Upraszczając ten wzór, otrzymujemy:

Pole sześciokąta = (3a²√3) / 2

Gdzie a oznacza długość boku sześciokąta foremnego, który jest jednocześnie bokiem podstawy graniastosłupa prawidłowego sześciokątnego.

Alternatywne podejścia do obliczania pola podstawy

Istnieją inne sposoby na dojście do tego samego wyniku, choć mniej intuicyjne. Możemy na przykład skorzystać z trygonometrii. Sześciokąt foremny można opisać na okręgu, a każdy z trójkątów równobocznych wspomnianych wcześniej można podzielić na dwa trójkąty prostokątne. Korzystając z funkcji trygonometrycznych, takich jak sinus i cosinus, możemy wyrazić wysokość trójkąta równobocznego w zależności od długości boku a.

Wysokość trójkąta równobocznego h można obliczyć ze wzoru:

h = (a√3) / 2

Następnie, znając wysokość i podstawę (czyli połowę boku a), możemy obliczyć pole jednego trójkąta równobocznego, a następnie pomnożyć je przez 6, aby uzyskać pole całego sześciokąta.

Innym podejściem jest rozważenie sześciokąta foremnego jako specjalnego przypadku wielokąta foremnego. Ogólny wzór na pole wielokąta foremnego o n bokach i długości boku a to:

P = (na²)/(4 * tg(π/n))

Podstawiając n = 6 (bo sześciokąt foremny ma 6 boków), otrzymujemy:

P = (6a²)/(4 * tg(π/6))

Ponieważ tg(π/6) = 1/√3, wzór upraszcza się do:

P = (6a²)/(4 * (1/√3)) = (6a²√3) / 4 = (3a²√3) / 2

Co jest dokładnie tym samym wzorem, który wyprowadziliśmy wcześniej.

Pamiętajmy, że a we wszystkich tych wzorach oznacza długość boku sześciokąta foremnego, czyli krawędź podstawy graniastosłupa. Jeśli znamy tylko inne parametry, takie jak promień okręgu opisanego na sześciokącie (R) lub promień okręgu wpisanego w sześciokąt (r), możemy je wykorzystać do obliczenia długości boku a, a następnie podstawić ją do wzoru na pole sześciokąta.

Związek między bokiem a, promieniem okręgu opisanego R i promieniem okręgu wpisanego r w sześciokąt foremny jest następujący:

• a = R
• r = (a√3) / 2

Możemy więc, mając dany promień okręgu opisanego R, podstawić go bezpośrednio za a we wzorze na pole sześciokąta. Natomiast jeśli mamy dany promień okręgu wpisanego r, musimy najpierw obliczyć długość boku a korzystając z powyższego wzoru:

a = (2r) / √3

Następnie podstawiamy obliczoną wartość a do wzoru na pole sześciokąta.

Podsumowując, obliczenie pola podstawy graniastosłupa prawidłowego sześciokątnego sprowadza się do obliczenia pola sześciokąta foremnego. Najprostszym i najczęściej stosowanym wzorem jest:

Pole sześciokąta = (3a²√3) / 2

Gdzie a to długość boku sześciokąta. Pamiętajmy o jednostkach – jeśli bok a jest podany w centymetrach, to pole będzie wyrażone w centymetrach kwadratowych.

Należy zaznaczyć, że znajomość pola podstawy jest kluczowa do obliczenia objętości graniastosłupa prawidłowego sześciokątnego. Objętość obliczamy mnożąc pole podstawy przez wysokość graniastosłupa.

Zatem:

Objętość = Pole podstawy * Wysokość = ((3a²√3) / 2) * H

Gdzie H oznacza wysokość graniastosłupa.

Zatem zrozumienie wzoru na pole podstawy graniastosłupa prawidłowego sześciokątnego jest fundamentalne w wielu zagadnieniach matematycznych i inżynierskich. Opanowanie tego wzoru, wraz z umiejętnością jego wyprowadzenia na różne sposoby, zapewni solidne podstawy do dalszej nauki.