Wzor Na Pole Podstawy Graniastoslupa

Zmagasz się z obliczeniami objętości i pola powierzchni graniastosłupów? Wiem, jak frustrujące może być zapamiętywanie wszystkich wzorów, szczególnie jeśli nie widzisz, jak to się przekłada na rzeczywiste zastosowania. Nie martw się, nie jesteś sam! Wiele osób ma podobne trudności, a moim celem jest, aby ta podróż przez wzór na pole podstawy graniastosłupa stała się dla Ciebie jasna i zrozumiała.

Spróbujmy to odczarować. Wyobraź sobie, że projektujesz pudełko na prezent, planujesz budowę domku dla ptaków, albo po prostu chcesz obliczyć, ile farby potrzebujesz do pomalowania filaru. W każdym z tych przypadków, zrozumienie, jak obliczyć pole podstawy graniastosłupa, staje się nieocenione. To nie tylko sucha teoria, to praktyczne narzędzie, które może Ci pomóc w wielu codziennych sytuacjach.

Czym jest Graniastosłup?

Zacznijmy od podstaw. Graniastosłup to bryła, która ma dwie identyczne i równoległe podstawy, połączone ścianami bocznymi, które są równoległobokami (najczęściej prostokątami). To ważne, żeby to zrozumieć, bo rodzaj podstawy determinuje, jak obliczymy jej pole.

Rodzaje Graniastosłupów

Graniastosłup prosty: Ściany boczne są prostopadłe do podstaw.
Graniastosłup pochyły: Ściany boczne nie są prostopadłe do podstaw.
Graniastosłup prawidłowy: Podstawa jest wielokątem foremnym (np. trójkąt równoboczny, kwadrat, pięciokąt foremny).

W dalszej części skupimy się na graniastosłupach prostych, ponieważ są one najczęściej spotykane i łatwiejsze w obliczeniach.

Wzór na Pole Podstawy – Kluczowa Rzecz

Kluczem do sukcesu jest zrozumienie, że wzór na pole podstawy graniastosłupa zależy od kształtu tej podstawy! Nie ma jednego uniwersalnego wzoru. To jak z gotowaniem – każdy przepis jest inny, w zależności od tego, co chcesz ugotować.

Przejdźmy przez najpopularniejsze przypadki:

Graniastosłup o Podstawie Trójkąta

Jeśli podstawa jest trójkątem, potrzebujemy wzoru na pole trójkąta. Najczęściej spotykane przypadki to:

Trójkąt dowolny: Pole = 1/2 * a * h, gdzie 'a' to długość podstawy trójkąta, a 'h' to wysokość opuszczona na tę podstawę.
Trójkąt prostokątny: Pole = 1/2 * a * b, gdzie 'a' i 'b' to długości przyprostokątnych.
Trójkąt równoboczny: Pole = (a² * √3) / 4, gdzie 'a' to długość boku trójkąta.

Przykład: Załóżmy, że mamy graniastosłup prosty, którego podstawą jest trójkąt prostokątny o przyprostokątnych długości 3 cm i 4 cm. Wtedy pole podstawy wynosi: 1/2 * 3 cm * 4 cm = 6 cm².

Graniastosłup o Podstawie Czworokąta

Tutaj mamy jeszcze więcej możliwości, w zależności od tego, jaki czworokąt stanowi podstawę:

Kwadrat: Pole = a², gdzie 'a' to długość boku kwadratu.
Prostokąt: Pole = a * b, gdzie 'a' i 'b' to długości boków prostokąta.
Równoległobok: Pole = a * h, gdzie 'a' to długość podstawy równoległoboku, a 'h' to wysokość opuszczona na tę podstawę.
Romb: Pole = (d1 * d2) / 2, gdzie 'd1' i 'd2' to długości przekątnych rombu. Albo Pole = a * h, gdzie 'a' to długość boku rombu, a 'h' to wysokość opuszczona na ten bok.
Trapez: Pole = ((a + b) * h) / 2, gdzie 'a' i 'b' to długości podstaw trapezu, a 'h' to wysokość trapezu.

Przykład: Mamy graniastosłup prosty o podstawie prostokąta o wymiarach 5 cm x 8 cm. Pole podstawy wynosi: 5 cm * 8 cm = 40 cm².

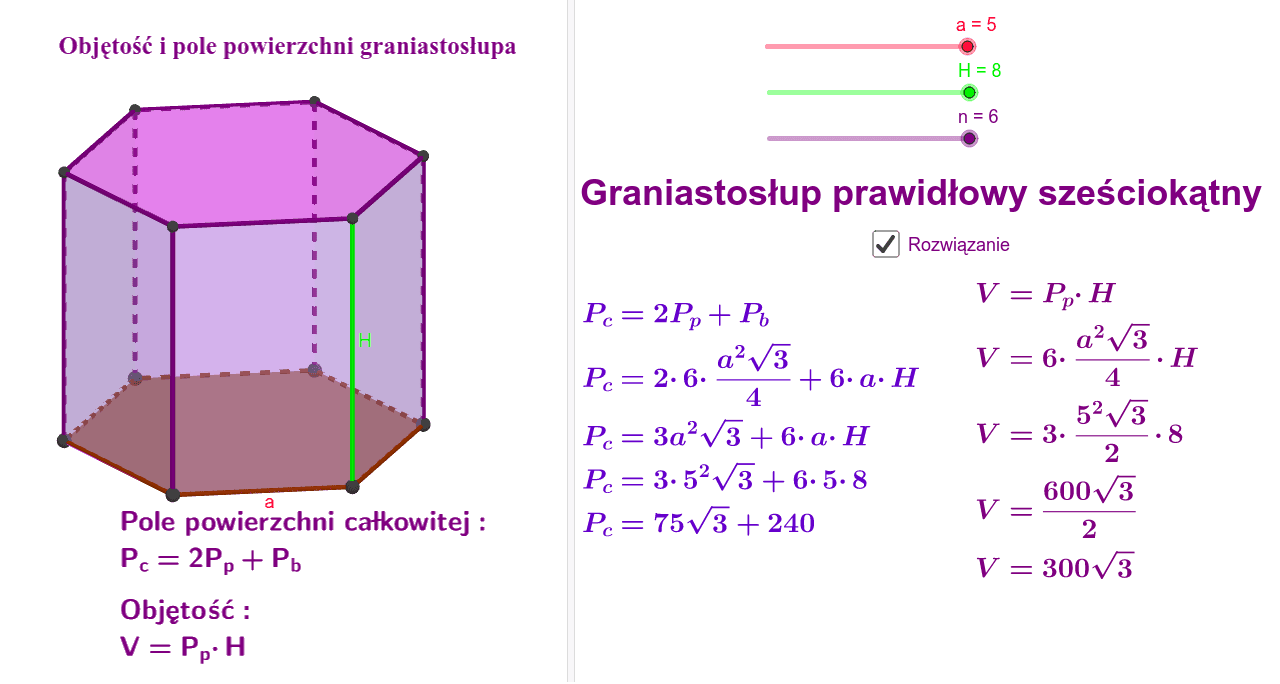
Graniastosłup o Podstawie Wielokąta Foremnym

Dla wielokątów foremnych (np. pięciokąt, sześciokąt foremny) wzór na pole staje się bardziej skomplikowany, ale można go znaleźć w tablicach matematycznych lub w internecie. Często stosuje się podział wielokąta na mniejsze figury (np. trójkąty) i sumuje ich pola.

Przykład: Sześciokąt foremny można podzielić na 6 trójkątów równobocznych. Jeśli znamy długość boku sześciokąta (czyli boku każdego z trójkątów), możemy obliczyć pole każdego trójkąta i pomnożyć wynik przez 6.

Obalamy Mity i Rozpraszamy Wątpliwości

Często słyszę: "Matematyka jest bezużyteczna" albo "Nigdy tego nie wykorzystam". Może to prawda, jeśli patrzysz na to tylko jak na serię wzorów do zapamiętania. Ale zrozumienie zasad obliczania pola podstawy graniastosłupa rozwija Twoje myślenie przestrzenne, umiejętność rozwiązywania problemów i logiczne rozumowanie. To umiejętności, które przydadzą się w wielu dziedzinach życia, nawet jeśli nie będziesz codziennie obliczać pól podstaw.

Inna wątpliwość: "Dlaczego muszę to robić ręcznie, skoro mogę użyć kalkulatora?". Oczywiście, kalkulator jest pomocny, ale ważne jest zrozumienie, co robisz. Kalkulator to tylko narzędzie. Bez zrozumienia podstaw, łatwo popełnić błąd i zaufać błędnemu wynikowi.

Praktyczne Zastosowania

Pomyśl o tych sytuacjach, w których obliczanie pola podstawy graniastosłupa jest przydatne:

Budownictwo: Obliczanie ilości materiałów potrzebnych do budowy filarów, dachów o nietypowym kształcie.
Projektowanie: Określanie wymiarów opakowań, pudełek, pojemników.
Inżynieria: Projektowanie mostów, tuneli, innych konstrukcji inżynieryjnych.
Architektura krajobrazu: Planowanie rabat kwiatowych o nietypowych kształtach.
Życie codzienne: Obliczanie ile farby potrzebujesz do pomalowania ściany, która ma kształt graniastosłupa.

To tylko kilka przykładów. Im lepiej rozumiesz geometrię, tym łatwiej poradzisz sobie z różnymi problemami w życiu codziennym i zawodowym.

Krok po Kroku – Jak Obliczyć Pole Podstawy Graniastosłupa

Oto kilka kroków, które pomogą Ci w obliczeniach:

Zidentyfikuj kształt podstawy. Czy to trójkąt, kwadrat, prostokąt, trapez, czy inny wielokąt?
Znajdź odpowiedni wzór na pole figury geometrycznej, która stanowi podstawę.
Zmierz lub odczytaj wymiary potrzebne do obliczenia pola (np. długość boku, wysokość, przekątne).
Podstaw wartości do wzoru i oblicz pole.
Pamiętaj o jednostkach! Pole zawsze wyrażamy w jednostkach kwadratowych (np. cm², m², itd.).

Podsumowanie i Co Dalej?

Obliczanie pola podstawy graniastosłupa nie musi być straszne! Pamiętaj, że kluczem jest zrozumienie podstawowych wzorów na pola figur geometrycznych i umiejętność ich zastosowania. Ćwicz regularnie, rozwiązuj zadania, a zobaczysz, że stanie się to coraz łatwiejsze.

Najważniejsze: Nie bój się pytać! Jeśli masz wątpliwości, szukaj pomocy w podręcznikach, w internecie, albo zapytaj nauczyciela lub kogoś, kto dobrze rozumie matematykę.

Czy po przeczytaniu tego artykułu czujesz się bardziej pewnie w obliczaniu pola podstawy graniastosłupa? A może masz jeszcze jakieś pytania? Spróbuj rozwiązać kilka zadań praktycznych. Powodzenia!