Wzór Na Pole Dowolnego Czworokąta

Czy kiedykolwiek stanąłeś przed problemem obliczenia pola powierzchni nieregularnego kawałka ziemi, dziwnego kształtu blatu, czy nawet skomplikowanego elementu architektonicznego? Jeśli tak, z pewnością wiesz, jak frustrujące może być szukanie odpowiedniego wzoru. Większość z nas pamięta wzory na pole kwadratu, prostokąta czy trójkąta, ale co zrobić, gdy mamy do czynienia z czworokątem, który nie jest ani jednym, ani drugim?

Spokojnie, nie jesteś sam! Obliczanie pola dowolnego czworokąta może wydawać się wyzwaniem, ale w rzeczywistości istnieje kilka metod, które pozwalają nam sobie z tym poradzić. W tym artykule przyjrzymy się najpopularniejszym z nich, a także zrozumiemy, kiedy i którą metodę warto zastosować. Celem jest, abyś po przeczytaniu tego tekstu czuł się pewnie, mając przed sobą czworokąt o dowolnym kształcie!

Metody obliczania pola dowolnego czworokąta

Zanim przejdziemy do konkretnych wzorów, warto zaznaczyć, że "dowolny czworokąt" to bardzo szerokie pojęcie. Może to być trapez, deltoid, równoległobok, a nawet figura, która nie przypomina żadnej z tych dobrze znanych. Dlatego też nie istnieje jeden uniwersalny wzór, który zadziała w każdym przypadku. Niemniej jednak, istnieją metody, które możemy dostosować do konkretnej sytuacji.

Metoda podziału na trójkąty

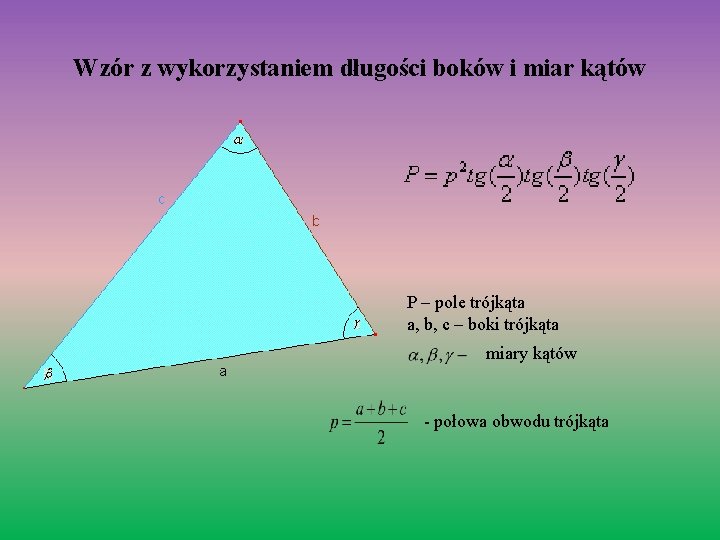
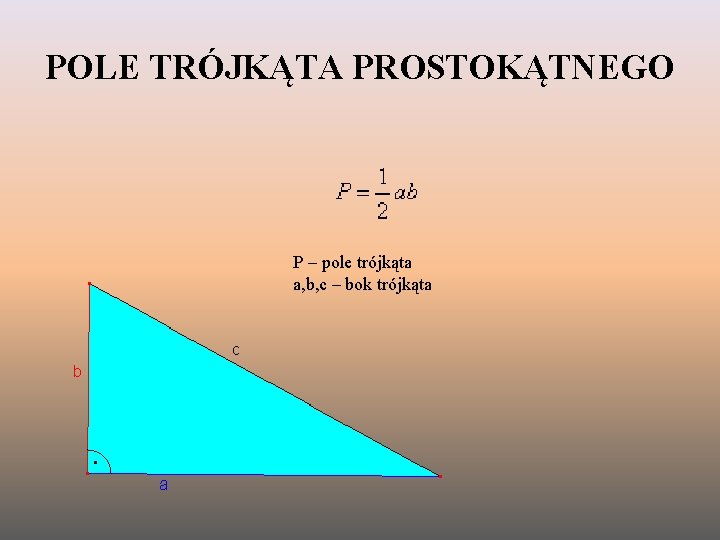
To jedna z najprostszych i najbardziej intuicyjnych metod. Polega na podzieleniu czworokąta na dwa trójkąty poprzez narysowanie przekątnej. Następnie obliczamy pole każdego z trójkątów oddzielnie i sumujemy je. Brzmi prosto, prawda? Ale jak obliczyć pole trójkąta, jeśli nie znamy jego wysokości?

Wzór Herona: Jeśli znamy długości wszystkich trzech boków trójkąta (a, b, c), możemy skorzystać z wzoru Herona:

P = √(s(s-a)(s-b)(s-c)),

gdzie s to połowa obwodu trójkąta (s = (a + b + c) / 2).

Wzór z sinusem kąta: Jeśli znamy długości dwóch boków trójkąta (a, b) i kąt między nimi (γ), możemy użyć wzoru:

P = (1/2) * a * b * sin(γ)

Przykład: Wyobraź sobie czworokąt ABCD. Narysuj przekątną AC. Teraz masz dwa trójkąty: ABC i ACD. Zmierz długości boków AB, BC, AC, AD, CD. Używając wzoru Herona, oblicz pole trójkąta ABC, a następnie pole trójkąta ACD. Zsumuj te dwa pola, aby otrzymać pole czworokąta ABCD.

Wzór Bretschneidera

Wzór Bretschneidera to bardziej zaawansowane narzędzie, które pozwala obliczyć pole dowolnego czworokąta, znając długości jego boków i sumę dwóch przeciwległych kątów. Wygląda on następująco:

P = √((s - a)(s - b)(s - c)(s - d) - abcd * cos²((α + γ) / 2)),

gdzie a, b, c, d to długości boków czworokąta, α i γ to dwa przeciwległe kąty, a s to połowa obwodu czworokąta (s = (a + b + c + d) / 2).

Kiedy stosować wzór Bretschneidera? Najlepiej sprawdza się, gdy zmierzenie kątów jest łatwiejsze niż wyznaczenie wysokości w metodzie podziału na trójkąty. Jest to szczególnie przydatne w geodezji i kartografii, gdzie pomiar kątów jest często bardziej precyzyjny niż pomiar odległości.

Zauważmy: Jeśli α + γ = 180° (czyli czworokąt jest wpisany w okrąg), wzór Bretschneidera upraszcza się do wzoru Brahmaghupty:

P = √((s - a)(s - b)(s - c)(s - d))

Pole czworokąta opisanego na okręgu

Jeśli czworokąt jest opisany na okręgu (co oznacza, że okrąg jest styczny do wszystkich jego boków), możemy skorzystać z uproszczonego wzoru:

P = √(abcd)

gdzie a, b, c, d to długości boków czworokąta.

Ważne zastrzeżenie: Niewiele czworokątów spełnia warunek bycia opisanym na okręgu. Upewnij się, że rzeczywiście masz do czynienia z takim czworokątem, zanim zastosujesz ten wzór. Jak to sprawdzić? Sumy długości przeciwległych boków muszą być równe (a + c = b + d).

Przypadki szczególne: Wzory na znane czworokąty

Oczywiście, jeśli mamy do czynienia ze znanym typem czworokąta, możemy skorzystać z dedykowanych wzorów:

Kwadrat: P = a² (gdzie a to długość boku)
Prostokąt: P = a * b (gdzie a i b to długości boków)
Równoległobok: P = a * h (gdzie a to długość boku, a h to wysokość opuszczona na ten bok) lub P = a * b * sin(α) (gdzie a i b to długości boków, a α to kąt między nimi)
Romb: P = (1/2) * d1 * d2 (gdzie d1 i d2 to długości przekątnych)
Trapez: P = (1/2) * (a + b) * h (gdzie a i b to długości podstaw, a h to wysokość)
Deltoid: P = (1/2) * d1 * d2 (gdzie d1 i d2 to długości przekątnych)

Pamiętaj: Zidentyfikowanie rodzaju czworokąta znacząco upraszcza obliczenia!

Praktyczne wskazówki i narzędzia

Obliczanie pola dowolnego czworokąta może być żmudne, szczególnie jeśli mamy do czynienia z wieloma pomiarami i skomplikowanymi wzorami. Dlatego warto skorzystać z dostępnych narzędzi:

Kalkulatory online: Istnieje wiele kalkulatorów online, które pozwalają obliczyć pole czworokąta po wprowadzeniu odpowiednich danych (długości boków, kątów, przekątnych). Wystarczy poszukać w internecie frazy "kalkulator pola czworokąta".
Oprogramowanie CAD: Programy do projektowania wspomaganego komputerowo (CAD) pozwalają na precyzyjne rysowanie i mierzenie obiektów, w tym czworokątów. Są szczególnie przydatne w architekturze i inżynierii.
Aplikacje na smartfony: Istnieją aplikacje, które wykorzystują aparat smartfona do pomiaru odległości i kątów, co może być pomocne w obliczaniu pola czworokąta w terenie.

Dodatkowe wskazówki:

Dokładność pomiarów: Im dokładniejsze pomiary, tym dokładniejszy wynik. Używaj precyzyjnych narzędzi pomiarowych.
Rysunek pomocniczy: Zawsze warto narysować czworokąt, nawet jeśli jest to szkic odręczny. Pomoże to w zrozumieniu geometrii problemu i wyborze odpowiedniej metody.
Sprawdzanie wyniku: Po obliczeniu pola, warto zastanowić się, czy uzyskany wynik jest sensowny. Czy pole jest dodatnie? Czy jest rzędu wielkości, którego się spodziewaliśmy?

Podsumowanie

Obliczanie pola dowolnego czworokąta nie musi być trudne. Kluczem jest zrozumienie różnych metod i umiejętność ich zastosowania w zależności od dostępnych danych. Metoda podziału na trójkąty jest uniwersalna i intuicyjna, ale wymaga pomiaru długości boków i ewentualnie kątów. Wzór Bretschneidera jest bardziej zaawansowany, ale przydatny, gdy łatwiej zmierzyć kąty. Pamiętaj o istnieniu dedykowanych wzorów dla znanych typów czworokątów. A przede wszystkim, korzystaj z dostępnych narzędzi, które mogą ułatwić obliczenia.

Mając tę wiedzę, jesteś teraz dobrze przygotowany, aby poradzić sobie z obliczeniem pola dowolnego czworokąta. Powodzenia!