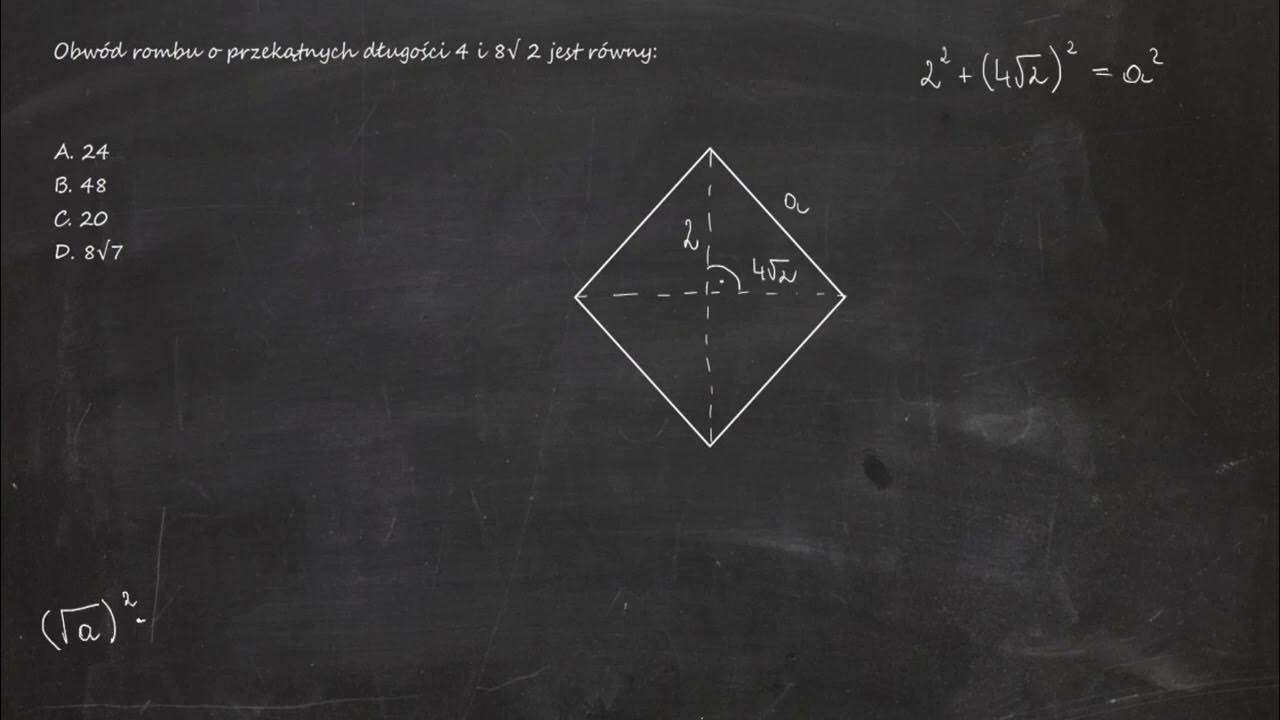Wzór Na Obwód Rombu Z Przekątnych

Wielu uczniów i studentów zastanawia się, jak obliczyć obwód rombu, znając jedynie długości jego przekątnych. Choć bezpośredni wzór na obwód rombu wykorzystujący przekątne nie istnieje, możliwe jest jego obliczenie poprzez wykorzystanie twierdzenia Pitagorasa i relacji między przekątnymi rombu a jego bokiem. W tym artykule szczegółowo omówimy proces obliczania obwodu rombu na podstawie długości jego przekątnych.

Wprowadzenie do Rombu

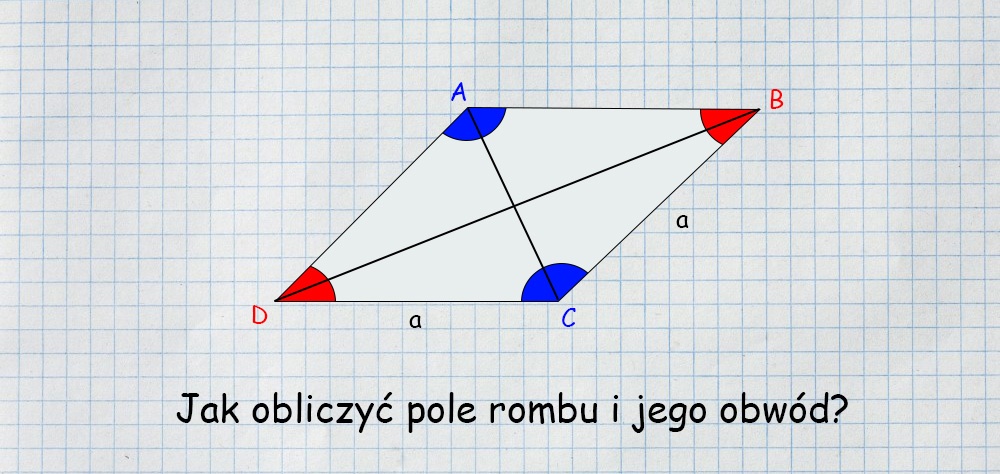
Romb to specjalny rodzaj równoległoboku, który charakteryzuje się kilkoma kluczowymi cechami:

• Wszystkie cztery boki mają równą długość.
• Przeciwległe kąty są równe.
• Przekątne przecinają się pod kątem prostym.
• Przekątne dzielą się na połowy w punkcie przecięcia.

Zrozumienie tych właściwości jest kluczowe do obliczenia obwodu rombu przy użyciu długości jego przekątnych.

Dlaczego Nie Ma Bezpośredniego Wzoru?

W przeciwieństwie do kwadratu, gdzie obwód (O) można łatwo obliczyć jako O = 4a (gdzie 'a' to długość boku), romb nie posiada tak prostego wzoru opartego bezpośrednio na długości przekątnych (p i q). Wynika to z faktu, że przekątne, choć przecinają się pod kątem prostym i dzielą na połowy, nie są bezpośrednio proporcjonalne do długości boku w sposób, który pozwoliłby na stworzenie prostego wzoru. Konieczne jest wykorzystanie twierdzenia Pitagorasa.

Wykorzystanie Twierdzenia Pitagorasa

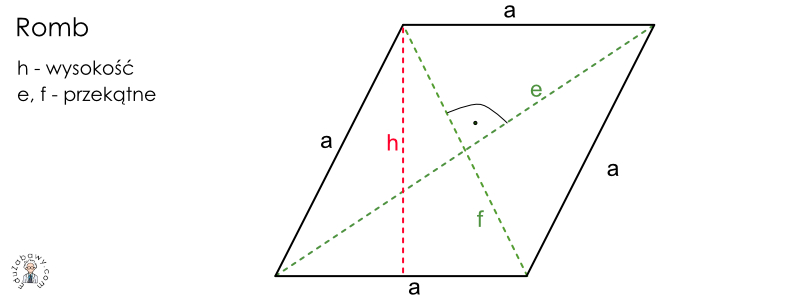
Klucz do obliczenia obwodu rombu, znając jego przekątne, leży w wykorzystaniu twierdzenia Pitagorasa. Przekątne rombu dzielą go na cztery przystające trójkąty prostokątne. Boki tych trójkątów prostokątnych to połowy przekątnych rombu, a przeciwprostokątną jest bok rombu.

Niech:

• p oznacza długość jednej przekątnej.
• q oznacza długość drugiej przekątnej.
• a oznacza długość boku rombu.

Wówczas, połowy przekątnych wynoszą p/2 i q/2. Zgodnie z twierdzeniem Pitagorasa:

a² = (p/2)² + (q/2)²

Stąd, długość boku rombu a wynosi:

a = √((p/2)² + (q/2)²)

Obliczanie Obwodu

Ponieważ obwód rombu (O) to suma długości wszystkich jego boków, a romb ma 4 równe boki, wzór na obwód rombu wygląda następująco:

O = 4a

Podstawiając wzór na długość boku a, otrzymujemy:

O = 4 * √((p/2)² + (q/2)²)

Możemy to uprościć do:

O = 2 * √(p² + q²)

Ten wzór pozwala obliczyć obwód rombu na podstawie długości jego przekątnych.

Przykład Obliczeniowy

Załóżmy, że mamy romb, którego przekątne mają długości p = 6 cm i q = 8 cm. Chcemy obliczyć jego obwód.

1. Oblicz kwadraty długości przekątnych: p² = 6² = 36 cm² i q² = 8² = 64 cm².
2. Dodaj kwadraty długości przekątnych: 36 cm² + 64 cm² = 100 cm².
3. Oblicz pierwiastek kwadratowy z sumy kwadratów: √100 cm² = 10 cm.
4. Pomnóż wynik przez 2: 2 * 10 cm = 20 cm.

Zatem, obwód rombu wynosi 20 cm.

Real-World Examples

Choć może się wydawać, że obliczanie obwodu rombu to czysto akademickie ćwiczenie, istnieje wiele sytuacji w życiu codziennym i inżynierii, gdzie ta wiedza może być przydatna. Oto kilka przykładów:

• Architektura: W projektowaniu dekoracyjnych elementów budynków, takich jak wzory na podłogach lub elewacjach, często wykorzystywane są romby. Obliczenie obwodu rombu może być potrzebne do oszacowania ilości materiału potrzebnego do stworzenia takiego elementu.
• Inżynieria: W konstrukcjach kratownicowych, romby mogą być używane jako elementy wzmacniające. Znajomość obwodu rombu pozwala na obliczenie długości potrzebnych prętów i optymalizację konstrukcji.
• Projektowanie biżuterii: Romb jest popularnym kształtem w projektowaniu biżuterii. Obliczenie obwodu rombu jest kluczowe do oszacowania ilości metalu potrzebnego do wykonania danej ozdoby.
• Grafika komputerowa: W tworzeniu grafiki komputerowej, zwłaszcza w grach, często wykorzystuje się obiekty geometryczne, w tym romby. Obliczenie obwodu rombu może być potrzebne do optymalizacji renderingu i zapewnienia płynności działania aplikacji.

Na przykład, wyobraźmy sobie firmę produkującą panele podłogowe w kształcie rombów. Muszą oni oszacować ilość materiału potrzebną do wyprodukowania określonej liczby paneli. Znając długości przekątnych każdego rombu, mogą obliczyć jego obwód, a następnie obliczyć całkowitą długość krawędzi, którą trzeba wyciąć z płyty materiału. To z kolei pozwala na precyzyjne oszacowanie kosztów materiałowych i minimalizację odpadów.

Typowe Błędy i Jak ich Unikać

Podczas obliczania obwodu rombu z przekątnych, uczniowie często popełniają następujące błędy:

• Zapominanie o podzieleniu przekątnych przez 2: Pamiętaj, że w twierdzeniu Pitagorasa używamy połówek długości przekątnych, a nie ich pełnych długości.
• Błędne zastosowanie twierdzenia Pitagorasa: Upewnij się, że prawidłowo identyfikujesz boki i przeciwprostokątną w trójkącie prostokątnym utworzonym przez przekątne rombu.
• Zapominanie o pomnożeniu długości boku przez 4: Obwód to suma długości wszystkich czterech boków, więc nie zapomnij pomnożyć obliczonej długości boku przez 4.
• Błędy w obliczeniach: Sprawdź dokładnie swoje obliczenia, zwłaszcza podczas obliczania pierwiastka kwadratowego.

Aby uniknąć tych błędów, zawsze rysuj diagram rombu i oznaczaj na nim długości przekątnych oraz połowy długości przekątnych. Sprawdzaj swoje obliczenia krok po kroku i upewnij się, że rozumiesz, co robisz.

Podsumowanie

Obliczanie obwodu rombu na podstawie długości jego przekątnych wymaga zastosowania twierdzenia Pitagorasa i zrozumienia relacji między przekątnymi a bokiem rombu. Choć nie istnieje bezpośredni wzór wykorzystujący wyłącznie przekątne, można obliczyć długość boku rombu, a następnie pomnożyć ją przez 4, aby uzyskać obwód. Wzór, który należy zapamiętać, to: O = 2 * √(p² + q²), gdzie p i q to długości przekątnych.

Pamiętaj o kluczowych krokach: podziel przekątne przez 2, zastosuj twierdzenie Pitagorasa, oblicz pierwiastek kwadratowy i pomnóż wynik przez 4 (lub 2, jeśli korzystasz z uproszczonego wzoru). Zrozumienie tych zasad pozwoli Ci z łatwością obliczać obwody rombów w różnych sytuacjach.

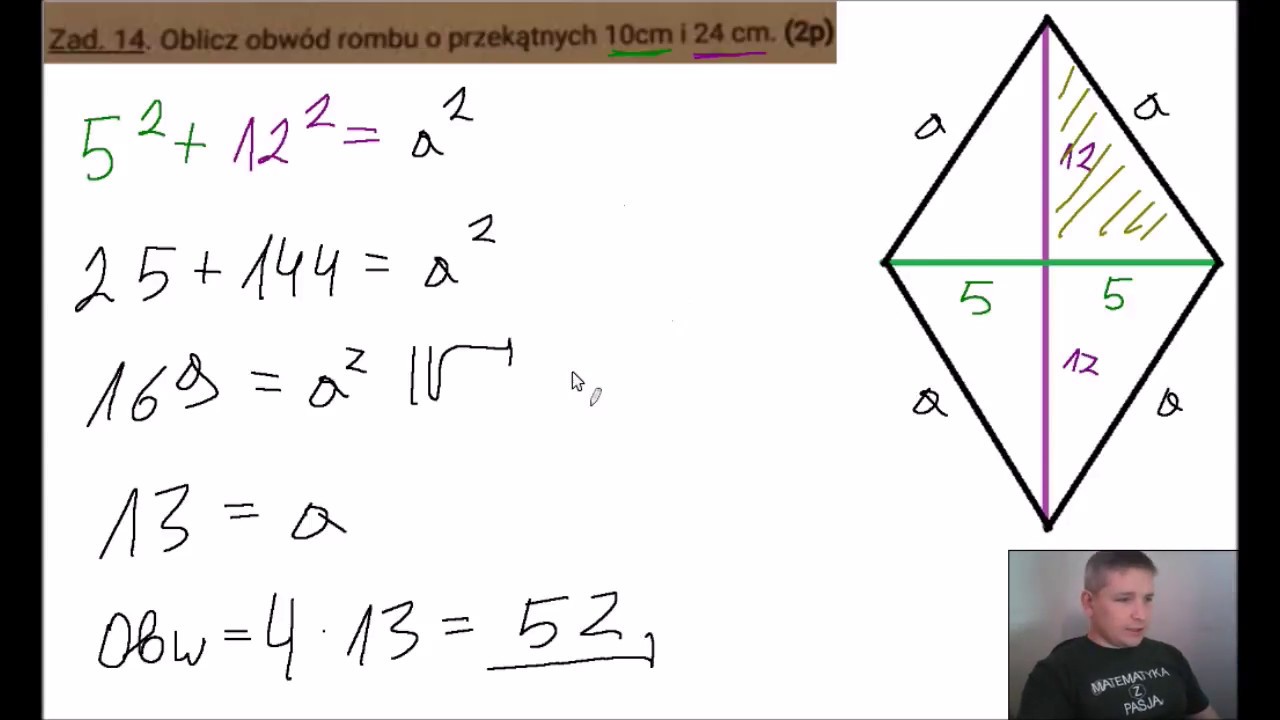
Zadanie Dla Ciebie

Spróbuj obliczyć obwód rombu, którego przekątne mają długości 10 cm i 24 cm. Sprawdź, czy rozumiesz omówiony proces. Podziel się swoim wynikiem! To doskonały sposób na utrwalenie wiedzy.