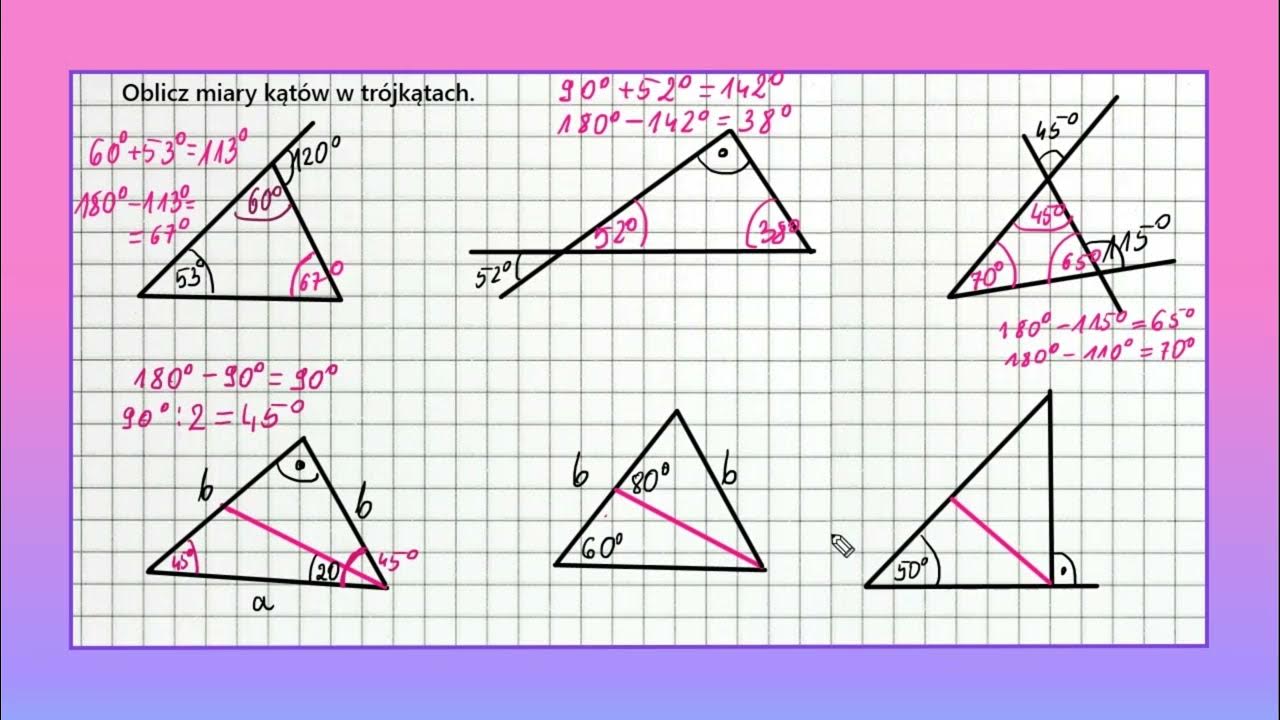
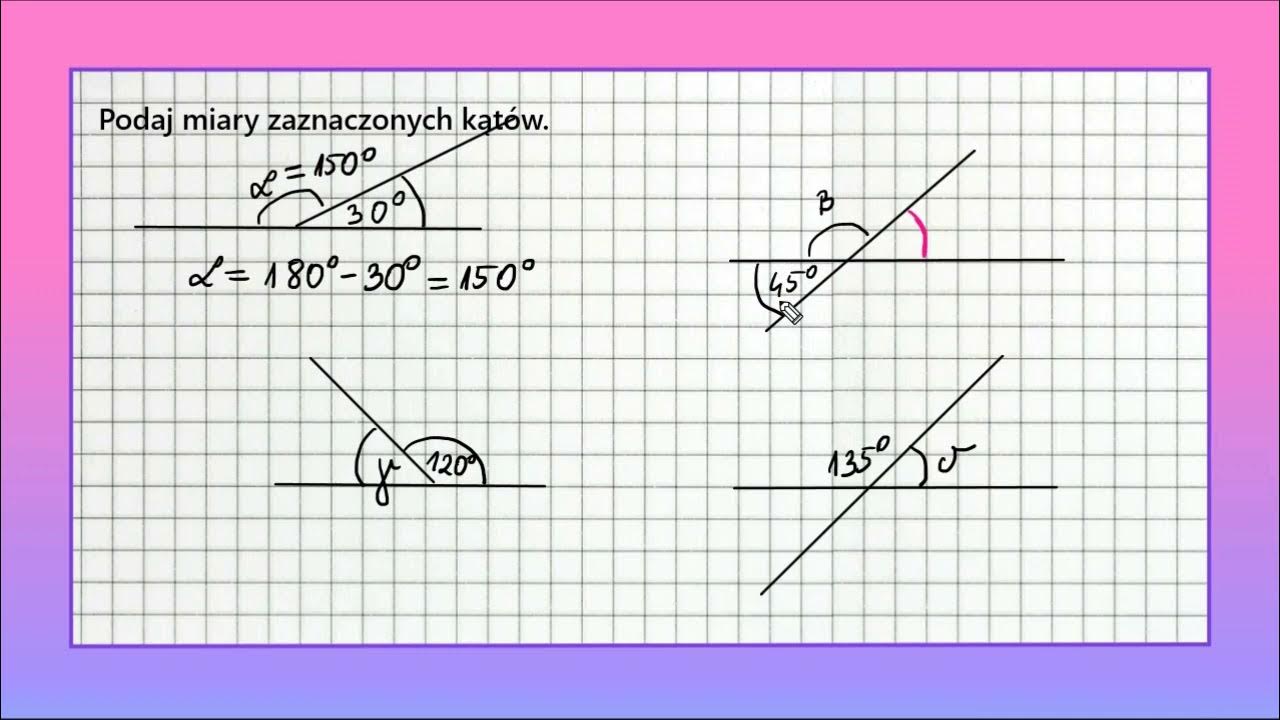
Wzór Na Miarę Kąta Wewnętrznego

Geometria, dział matematyki zajmujący się kształtami, rozmiarami, względnymi pozycjami figur oraz właściwościami przestrzeni, oferuje bogaty zbiór narzędzi do analizy i zrozumienia otaczającego nas świata. Jednym z fundamentalnych pojęć w geometrii, szczególnie przy badaniu wielokątów, jest miara kąta wewnętrznego. Zrozumienie i obliczanie tych kątów jest niezbędne w wielu dziedzinach, od architektury po grafikę komputerową.

Wprowadzenie do Kątów Wewnętrznych

Kąt wewnętrzny wielokąta to kąt utworzony przez dwie sąsiednie krawędzie tego wielokąta wewnątrz jego figury. Przykładowo, w trójkącie każdy z trzech kątów wewnątrz trójkąta jest kątem wewnętrznym. Podobnie, w kwadracie każdy z czterech kątów prostych jest kątem wewnętrznym. Warto zauważyć, że kąty wewnętrzne, razem z kątami zewnętrznymi, tworzą kompletny obraz kątów związanych z danym wielokątem. Zrozumienie ich zależności jest kluczowe.

Definicja Wielokąta i jego Rodzaje

Zanim przejdziemy do wzoru, zdefiniujmy, czym jest wielokąt. Wielokąt to figura geometryczna płaska, ograniczona linią łamaną zamkniętą, składającą się z odcinków zwanych bokami. Wielokąty dzielimy na różne rodzaje, w zależności od liczby boków oraz od ich właściwości:

Trójkąty: Mają trzy boki.
Czworokąty: Mają cztery boki (np. kwadrat, prostokąt, trapez).
Pięciokąty: Mają pięć boków.
Sześciokąty: Mają sześć boków.
... i tak dalej, dla dowolnej liczby boków.

Wielokąty mogą być również wypukłe (gdzie każdy kąt wewnętrzny jest mniejszy niż 180 stopni) lub wklęsłe (gdzie przynajmniej jeden kąt wewnętrzny jest większy niż 180 stopni). Rozróżnienie to ma znaczenie, chociaż wzór, o którym będziemy mówić, działa dla obu typów.

Wzór na Sumę Kątów Wewnętrznych Wielokąta

Kluczowym elementem do obliczenia miary pojedynczego kąta wewnętrznego jest wzór na sumę wszystkich kątów wewnętrznych wielokąta. Brzmi on następująco:

S = (n - 2) * 180°

Gdzie:

S to suma miar kątów wewnętrznych.
n to liczba boków wielokąta.

Wzór ten wynika z możliwości podziału dowolnego wielokąta na trójkąty. Z każdego wierzchołka możemy poprowadzić przekątne do wszystkich innych wierzchołków, z wyjątkiem dwóch sąsiadujących. Liczba powstałych trójkątów jest zawsze o dwa mniejsza niż liczba boków wielokąta. Ponieważ suma kątów w trójkącie wynosi 180°, mnożąc (n-2) przez 180° otrzymujemy sumę kątów w całym wielokącie.

Obliczanie Miary Pojedynczego Kąta Wewnętrznego w Wielokącie Foremnym

W przypadku wielokątów foremnych (wielokątów, które mają wszystkie boki i wszystkie kąty równe), możemy pójść o krok dalej i obliczyć miarę pojedynczego kąta wewnętrznego. Wystarczy, że sumę wszystkich kątów wewnętrznych (obliczoną wzorem powyżej) podzielimy przez liczbę boków (n):

Miara pojedynczego kąta = [(n - 2) * 180°] / n

Na przykład, dla kwadratu (wielokąta foremnego o 4 bokach):

Miara pojedynczego kąta = [(4 - 2) * 180°] / 4 = (2 * 180°) / 4 = 360° / 4 = 90°

Co potwierdza, że każdy kąt wewnętrzny w kwadracie ma 90 stopni.

Przykłady Obliczeń

Rozważmy kilka przykładów, aby utrwalić zrozumienie wzoru.

Przykład 1: Pięciokąt Foremnym

Dla pięciokąta foremnego (n = 5):

Suma kątów wewnętrznych: S = (5 - 2) * 180° = 3 * 180° = 540°
Miara pojedynczego kąta: Miara pojedynczego kąta = 540° / 5 = 108°

Zatem każdy kąt wewnętrzny w pięciokącie foremnym ma miarę 108 stopni.

Przykład 2: Sześciokąt Foremnym

Dla sześciokąta foremnego (n = 6):

Suma kątów wewnętrznych: S = (6 - 2) * 180° = 4 * 180° = 720°
Miara pojedynczego kąta: Miara pojedynczego kąta = 720° / 6 = 120°

Zatem każdy kąt wewnętrzny w sześciokącie foremnym ma miarę 120 stopni.

Przykład 3: Wielokąt o 10 Bokach (Dekagon)

Dla dekagonu (n = 10):

Suma kątów wewnętrznych: S = (10 - 2) * 180° = 8 * 180° = 1440°
Miara pojedynczego kąta (jeśli jest foremny): Miara pojedynczego kąta = 1440° / 10 = 144°

Zatem suma kątów wewnętrznych w dekagonie wynosi 1440 stopni, a jeśli dekagon jest foremny, każdy kąt ma miarę 144 stopni.

Zastosowania w Praktyce

Wiedza o miarach kątów wewnętrznych znajduje szerokie zastosowanie w różnych dziedzinach:

Architektura i Budownictwo: Architekci i inżynierowie muszą precyzyjnie obliczać kąty, aby konstruować stabilne i estetyczne budynki. Na przykład, projektowanie dachu wymaga dokładnej znajomości kątów nachylenia, a w przypadku konstrukcji wielobocznych, znajomość kątów wewnętrznych jest niezbędna.
Grafika Komputerowa i Projektowanie Gier: Przy tworzeniu modeli 3D i wirtualnych środowisk, programiści i graficy używają geometrii do definiowania kształtów i powierzchni. Obliczanie kątów jest kluczowe dla renderowania realistycznych obrazów i interakcji w grach.
Inżynieria: Projektowanie maszyn, robotów i innych urządzeń wymaga precyzyjnego określania kątów, aby zapewnić prawidłowe działanie i uniknąć kolizji.
Geodezja i Kartografia: Pomiar i odwzorowywanie terenu wymaga dokładnych obliczeń kątów i odległości.

Rozważmy przykład z architektury. Projektując budynek o podstawie sześciokąta foremnego, architekt musi wiedzieć, że każdy kąt wewnętrzny w podstawie ma 120 stopni. Ta wiedza jest kluczowa do prawidłowego zaprojektowania ścian i dachu, aby zapewnić stabilność i estetykę konstrukcji.

Innym przykładem jest projektowanie płytek ceramicznych. Płytki sześciokątne są popularne, ponieważ można nimi pokryć płaszczyznę bez żadnych przerw. Dzieje się tak, ponieważ kąt wewnętrzny sześciokąta foremnego (120 stopni) jest podzielny przez 360 stopni (pełny kąt), co pozwala na idealne dopasowanie płytek.

Wzory dla Wielokątów Nieregularnych

W przypadku wielokątów nieregularnych, gdzie kąty i boki nie są równe, nie możemy użyć prostego wzoru na obliczenie miary pojedynczego kąta. W takim przypadku, musimy zmierzyć każdy kąt indywidualnie za pomocą kątomierza lub innych narzędzi pomiarowych. Suma wszystkich kątów wewnętrznych nadal będzie zgodna ze wzorem S = (n - 2) * 180°, ale kąty będą miały różne miary.

Podsumowanie

Wzór na miarę kąta wewnętrznego wielokąta jest fundamentalnym narzędziem w geometrii, pozwalającym na obliczanie sumy kątów wewnętrznych oraz, w przypadku wielokątów foremnych, miary pojedynczego kąta. Zrozumienie tego wzoru i jego zastosowań jest kluczowe dla wielu dziedzin, od architektury po grafikę komputerową. Pamiętajmy, że wzór S = (n - 2) * 180° daje nam sumę wszystkich kątów, a miarę pojedynczego kąta w wielokącie foremnym obliczamy dzieląc tę sumę przez liczbę boków.

Zachęcamy do dalszego zgłębiania wiedzy z zakresu geometrii i do wykorzystywania zdobytej wiedzy w praktycznych zastosowaniach. Eksperymentuj z różnymi wielokątami, obliczaj ich kąty i odkrywaj fascynujący świat geometrii!