Wzór Na Liczbę Przekątnych W Wielokącie

Czy kiedykolwiek zastanawiałeś się, jak wiele przekątnych ma dany wielokąt? Może myślałeś o tym, rozwiązując zadanie z geometrii w szkole, albo próbując zaprojektować unikalny wzór architektoniczny. Zrozumienie tego zagadnienia może wydawać się trudne, ale w rzeczywistości jest prostsze niż myślisz. Chcemy Ci pomóc zrozumieć wzór na liczbę przekątnych w wielokącie, pokazując, jak przydatny może być on w różnych sytuacjach i dlaczego warto go znać.

Dlaczego liczenie przekątnych jest ważne?

Zastanawiasz się, po co komu wiedzieć, ile przekątnych ma siedmiokąt? To pytanie jest całkowicie uzasadnione! W rzeczywistości zrozumienie przekątnych wielokątów ma wiele zastosowań, często w miejscach, których byś się nie spodziewał.

Zastosowania w architekturze i inżynierii

Architekci i inżynierowie wykorzystują wiedzę o właściwościach geometrycznych figur, w tym o przekątnych, przy projektowaniu budynków, mostów i innych konstrukcji. Przekątne mogą wpływać na stabilność i wytrzymałość konstrukcji. Na przykład, kratownice stosowane w mostach i dachach wykorzystują przekątne elementy, aby rozłożyć obciążenia i zapobiec odkształceniom. Zrozumienie, jak liczba przekątnych zmienia się w zależności od liczby boków, pozwala na optymalizację konstrukcji pod względem materiałów i wytrzymałości.

Zastosowania w grafice komputerowej i projektowaniu gier

W grafice komputerowej i projektowaniu gier, wielokąty są podstawowym elementem reprezentacji obiektów. Algorytmy wykorzystujące przekątne mogą być używane do triangulacji wielokątów, co ułatwia rendering i analizę kształtów. Na przykład, podział wielokąta na trójkąty pozwala na łatwiejsze cieniowanie i teksturowanie powierzchni w trójwymiarowej przestrzeni. Znajomość liczby przekątnych pomaga optymalizować te procesy.

Zastosowania w sztuce i designie

Artyści i projektanci często wykorzystują geometryczne kształty i wzory w swoich pracach. Wiedza o przekątnych może pomóc w tworzeniu harmonijnych i estetycznych kompozycji. Na przykład, podział kwadratu na trójkąty przy pomocy przekątnych tworzy dynamiczny i interesujący wizualnie układ. Zrozumienie relacji między liczbą boków a liczbą przekątnych pozwala na eksperymentowanie z różnymi wzorami i kształtami.

Wzór na liczbę przekątnych – Krok po kroku

Sama definicja przekątnej jest prosta: to odcinek łączący dwa niesąsiadujące wierzchołki wielokąta. Teraz przejdźmy do sedna – jak obliczyć liczbę tych przekątnych. Na szczęście istnieje prosty wzór:

n(n - 3) / 2

Gdzie n to liczba boków (i wierzchołków) wielokąta.

Brzmi skomplikowanie? Spokojnie, rozłóżmy to na czynniki pierwsze:

n: To po prostu liczba boków Twojego wielokąta. Kwadrat ma 4 boki, pięciokąt ma 5 boków, itd.
n - 3: Odejmujesz 3 od liczby boków. Dlaczego 3? Ponieważ z każdego wierzchołka nie możesz poprowadzić przekątnej do samego siebie (1 wierzchołek) ani do dwóch sąsiednich wierzchołków (2 wierzchołki).
n(n - 3): Mnożysz liczbę boków przez wynik odejmowania.
/ 2: Dzielisz wynik przez 2. Dlaczego? Ponieważ w przeciwnym razie każdą przekątną policzylibyśmy dwa razy (raz z jednego końca i raz z drugiego).

Przykłady

Zobaczmy kilka przykładów w praktyce:

Kwadrat (n = 4): 4(4 - 3) / 2 = 4(1) / 2 = 2. Kwadrat ma 2 przekątne.
Pięciokąt (n = 5): 5(5 - 3) / 2 = 5(2) / 2 = 5. Pięciokąt ma 5 przekątnych.
Sześciokąt (n = 6): 6(6 - 3) / 2 = 6(3) / 2 = 9. Sześciokąt ma 9 przekątnych.

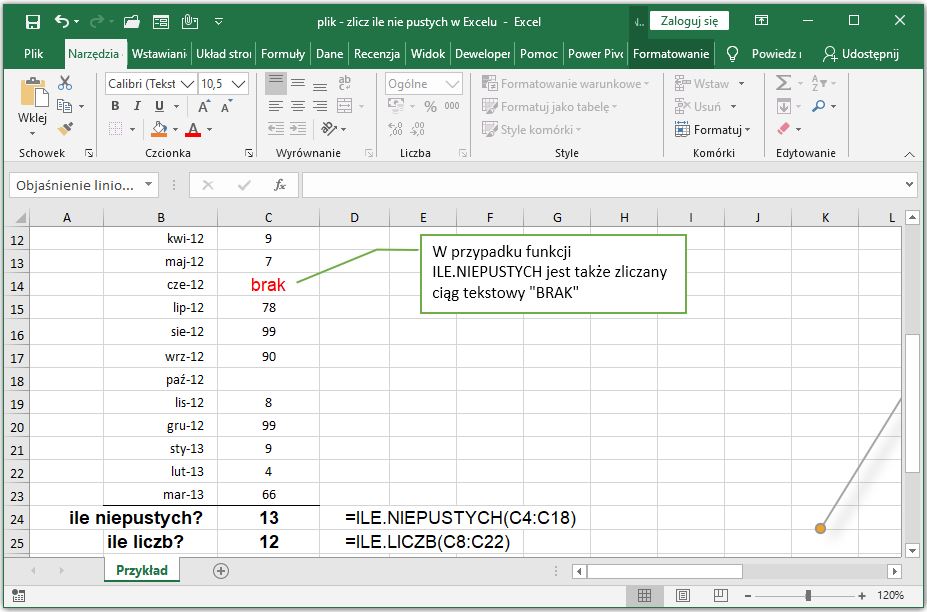
Spróbuj samodzielnie obliczyć liczbę przekątnych dla ośmiokąta (n=8) i dziesięciokąta (n=10)!

Skąd się wziął ten wzór?

Wzór n(n - 3) / 2 nie wziął się znikąd. Możemy go wyprowadzić, rozważając, ile przekątnych można narysować z każdego wierzchołka i korygując na podwójne zliczanie.

Z każdego wierzchołka wielokąta o n wierzchołkach można narysować (n - 3) przekątne, jak wyjaśniliśmy wcześniej. Jeśli pomnożymy liczbę wierzchołków (n) przez liczbę przekątnych z każdego wierzchołka (n - 3), otrzymamy n(n - 3). Jednak w ten sposób każda przekątna jest liczona dwukrotnie (raz dla każdego z jej końców), więc musimy podzielić wynik przez 2, aby otrzymać poprawną liczbę przekątnych: n(n - 3) / 2.

Czy zawsze się da? Kontrargumenty i wyjątki.

Wzór n(n - 3) / 2 działa doskonale dla wielokątów wypukłych. To znaczy takich, w których wszystkie kąty wewnętrzne są mniejsze niż 180 stopni. Jednak, gdy mamy do czynienia z wielokątami wklęsłymi (takimi, w których przynajmniej jeden kąt wewnętrzny jest większy niż 180 stopni), sytuacja staje się nieco bardziej złożona.

W wielokątach wklęsłych niektóre przekątne mogą leżeć poza obszarem figury. Wzór nadal podaje poprawną liczbę odcinków łączących niesąsiadujące wierzchołki, ale niektóre z tych odcinków nie są "przekątnymi" w intuicyjnym sensie, ponieważ znajdują się poza figurą.

Mimo to, wzór jest nadal przydatny, ponieważ pozwala określić liczbę wszystkich możliwych połączeń między niesąsiadującymi wierzchołkami, niezależnie od tego, czy leżą one wewnątrz czy na zewnątrz wielokąta.

Porady i triki

Zacznij od małych liczb: Jeśli masz problem z zapamiętaniem wzoru, spróbuj narysować kwadrat, pięciokąt i sześciokąt. Policz ręcznie przekątne, a następnie użyj wzoru, aby sprawdzić, czy wynik jest poprawny.
Używaj kalkulatora: Obliczanie z pamięci może być trudne, szczególnie dla większych liczb. Użyj kalkulatora, aby uniknąć błędów.
Pamiętaj o kolejności działań: Najpierw wykonaj odejmowanie w nawiasie (n - 3), następnie mnożenie, a na końcu dzielenie przez 2.

Podsumowanie i co dalej?

Zrozumienie wzoru na liczbę przekątnych w wielokącie to nie tylko kolejna umiejętność matematyczna. To narzędzie, które może być przydatne w wielu dziedzinach, od architektury i inżynierii po grafikę komputerową i sztukę. Mamy nadzieję, że dzięki temu artykułowi wzór n(n - 3) / 2 stał się dla Ciebie bardziej zrozumiały i przestanie być tajemnicą.

Pamiętaj, że matematyka to nie tylko suche liczby i wzory. To sposób myślenia i rozwiązywania problemów. Zachęcamy do dalszego zgłębiania tajników geometrii i odkrywania jej fascynujących zastosowań.

Czy zastanawiasz się teraz, jakie inne zagadnienia geometryczne mogą mieć zaskakujące zastosowania w Twoim życiu?