Wzor Na Droge W Ruchu Przyspieszonym

Ruch przyspieszony jest wszechobecny w naszym codziennym życiu, od startującego samolotu po spadające jabłko. Zrozumienie, jak obliczyć przebytą drogę w takim ruchu, jest kluczowe w fizyce i inżynierii. Niniejszy artykuł ma na celu szczegółowe omówienie wzoru na drogę w ruchu jednostajnie przyspieszonym, wyjaśnienie jego składowych oraz zaprezentowanie praktycznych zastosowań.

Kluczowe Elementy Ruchu Przyspieszonego

Zanim przejdziemy do samego wzoru, ważne jest zrozumienie podstawowych pojęć związanych z ruchem przyspieszonym. Omawiamy tutaj prędkość początkową, przyspieszenie i czas – elementy niezbędne do obliczenia przebytej drogi.

Prędkość Początkowa (v₀)

Prędkość początkowa (v₀) to prędkość, z jaką ciało rozpoczyna ruch w momencie rozpoczęcia obserwacji. Nie zawsze musi być równa zero. Na przykład, samochód może już poruszać się z pewną prędkością zanim zacznie przyspieszać. Jest to istotny parametr, który należy uwzględnić przy obliczaniu drogi.

Przyspieszenie (a)

Przyspieszenie (a) to zmiana prędkości w czasie. Jest to miara tego, jak szybko prędkość ciała się zmienia. Stałe przyspieszenie oznacza, że prędkość zmienia się równomiernie. Przyspieszenie może być dodatnie (wzrost prędkości) lub ujemne (opóźnienie, spadek prędkości). Jednostką przyspieszenia w układzie SI jest metr na sekundę kwadratową (m/s²).

Czas (t)

Czas (t) to interwał, w którym odbywa się ruch przyspieszony. Jest to okres, przez który ciało przyspiesza lub opóźnia się. Jednostką czasu w układzie SI jest sekunda (s).

Wzór na Drogę w Ruchu Jednostajnie Przyspieszonym

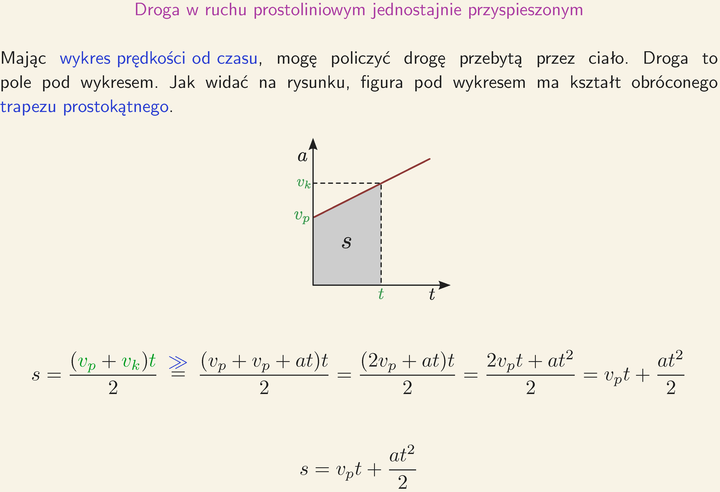
Wzór na drogę (s) w ruchu jednostajnie przyspieszonym ma postać:

s = v₀ * t + (1/2) * a * t²

Gdzie:

s to przebyta droga
v₀ to prędkość początkowa
t to czas trwania ruchu
a to przyspieszenie

Wzór ten uwzględnia zarówno wpływ prędkości początkowej, jak i przyspieszenia na przebytą drogę. Ważne jest, aby pamiętać o zachowaniu spójności jednostek podczas obliczeń.

Wyjaśnienie Wzoru Krok po Kroku

Wzór można rozłożyć na dwie części:

v₀ * t: Ta część reprezentuje drogę, jaką ciało przebyłoby, gdyby poruszało się ze stałą prędkością równą prędkości początkowej (v₀) przez czas (t).
(1/2) * a * t²: Ta część reprezentuje dodatkową drogę, jaką ciało przebywa dzięki przyspieszeniu (a) w czasie (t). Kwadrat czasu (t²) oznacza, że wpływ przyspieszenia na przebytą drogę rośnie kwadratowo z upływem czasu.

Przypadki Szczególne

Istnieją pewne szczególne przypadki, które warto rozważyć:

Prędkość Początkowa Równa Zero (v₀ = 0)

Jeśli ciało rozpoczyna ruch z prędkością początkową równą zero (np. rusza z miejsca), wzór upraszcza się do:

s = (1/2) * a * t²

Oznacza to, że droga zależy tylko od przyspieszenia i czasu.

Ruch Jednostajny (a = 0)

Jeśli przyspieszenie jest równe zero (ruch jednostajny), wzór redukuje się do:

s = v₀ * t

To jest znany wzór na drogę w ruchu jednostajnym prostoliniowym.

Opóźnienie (a < 0)

Jeśli przyspieszenie jest ujemne (opóźnienie), ciało zwalnia. Wzór pozostaje taki sam, ale wartość 'a' jest ujemna. Należy uważać na znaki podczas obliczeń, ponieważ opóźnienie zmniejsza przebytą drogę.

Przykłady Praktyczne

Aby lepiej zrozumieć wzór, rozważmy kilka przykładów:

Przykład 1: Samochód Przyspieszający

Samochód rusza z miejsca (v₀ = 0 m/s) i przyspiesza z przyspieszeniem a = 2 m/s² przez 5 sekund. Jaką drogę przebędzie?

Używamy wzoru: s = (1/2) * a * t² = (1/2) * 2 m/s² * (5 s)² = 25 metrów.

Samochód przebędzie 25 metrów.

Przykład 2: Rzut Pionowy w Górę

Piłka została wyrzucona pionowo w górę z prędkością początkową v₀ = 10 m/s. Przyspieszenie ziemskie wynosi g = -9.81 m/s² (ujemne, ponieważ działa przeciwnie do kierunku ruchu). Jaką drogę pokona piłka w ciągu 1 sekundy?

Używamy wzoru: s = v₀ * t + (1/2) * a * t² = 10 m/s * 1 s + (1/2) * (-9.81 m/s²) * (1 s)² = 10 m - 4.905 m = 5.095 metrów.

Piłka pokona 5.095 metrów w górę.

Przykład 3: Spadające Jabłko

Jabłko spada z drzewa (v₀ = 0 m/s). Przyspieszenie ziemskie wynosi g = 9.81 m/s². Jaką drogę przebędzie jabłko w ciągu 2 sekund?

Używamy wzoru: s = (1/2) * a * t² = (1/2) * 9.81 m/s² * (2 s)² = 19.62 metrów.

Jabłko przebędzie 19.62 metrów.

Zastosowania w Inżynierii i Fizyce

Wzór na drogę w ruchu przyspieszonym ma szerokie zastosowanie w różnych dziedzinach:

Inżynieria mechaniczna: Obliczanie odległości hamowania pojazdów, projektowanie układów zawieszenia.
Inżynieria lotnicza: Obliczanie drogi startowej samolotów, trajektorii lotu rakiet.
Fizyka: Analiza ruchu ciał w polu grawitacyjnym, modelowanie ruchu cząstek elementarnych.
Sport: Analiza wyników sportowych, optymalizacja technik ruchu (np. biegi, skoki).

Uwzględnianie Opory Powietrza

W rzeczywistości, w wielu sytuacjach występuje opór powietrza, który wpływa na ruch ciała. Wpływ ten jest pomijany w podstawowym wzorze na drogę w ruchu jednostajnie przyspieszonym. Uwzględnienie oporu powietrza znacznie komplikuje obliczenia i wymaga zastosowania bardziej zaawansowanych modeli matematycznych.

W przypadku obiektów o dużych powierzchniach i poruszających się z dużymi prędkościami (np. spadający spadochroniarz), opór powietrza staje się dominującą siłą i ciało osiąga prędkość graniczną, przy której siła oporu równoważy siłę grawitacji. W takim przypadku, ruch przestaje być jednostajnie przyspieszony i wzór na drogę w ruchu jednostajnie przyspieszonym przestaje być dokładny.

Podsumowanie

Wzór na drogę w ruchu jednostajnie przyspieszonym jest podstawowym narzędziem do analizy ruchu, w którym prędkość zmienia się w sposób jednostajny. Zrozumienie tego wzoru i jego składowych jest kluczowe dla wielu dziedzin nauki i techniki. Pamiętając o uwzględnianiu prędkości początkowej, przyspieszenia i czasu, można dokładnie obliczyć przebytą drogę w różnych scenariuszach.

Zachęcamy do eksperymentowania z różnymi wartościami prędkości początkowej, przyspieszenia i czasu, aby lepiej zrozumieć, jak te parametry wpływają na przebytą drogę. Wykorzystaj zdobytą wiedzę do rozwiązywania praktycznych problemów i analizy otaczającego Cię świata!