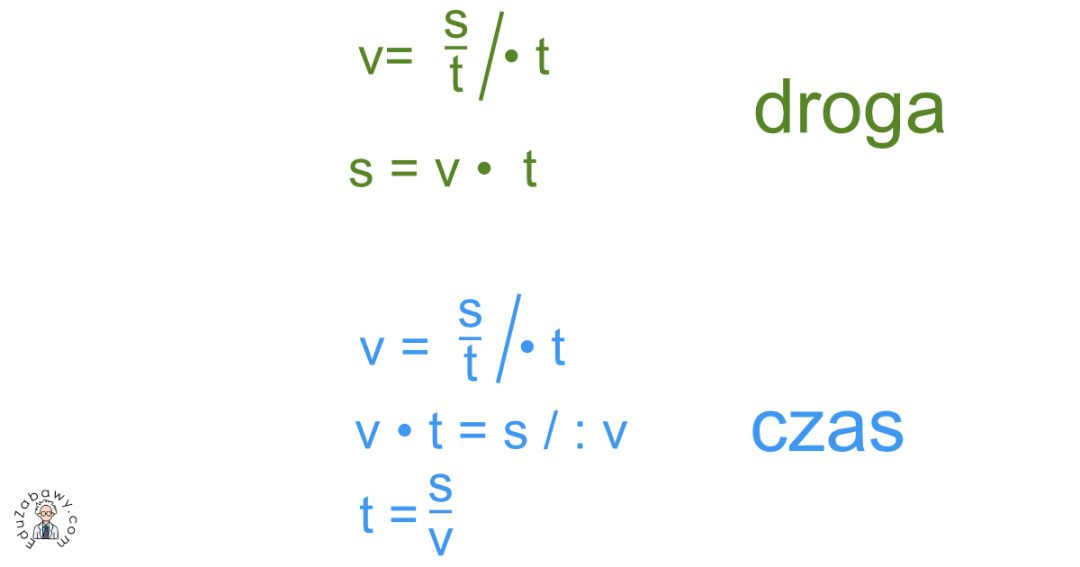Wzor Na Droge Predkosc Czas

Zastanawiałeś się kiedyś, ile czasu zajmie Ci dojazd do pracy, jeśli jedziesz z określoną prędkością? Albo jak daleko zajedziesz rowerem, jeśli wiesz, że możesz utrzymać konkretną szybkość przez daną ilość czasu? Odpowiedź na te pytania, i wiele innych, kryje się w jednym z fundamentalnych wzorów fizyki – wzorze na drogę, prędkość i czas. To podstawa, którą stosujemy w codziennym życiu, często nawet nie zdając sobie z tego sprawy. Spróbujmy to rozłożyć na czynniki pierwsze, tak żeby każdy mógł to zrozumieć i zastosować.

Podstawy: Czym jest droga, prędkość i czas?

Zacznijmy od definicji: czym właściwie są droga, prędkość i czas? Wyjaśnimy to sobie w sposób bardzo intuicyjny.

Droga (s)

Droga, oznaczana zazwyczaj literą "s" (od łacińskiego "spatium"), to po prostu długość trasy, którą pokonujemy. Mierzymy ją w różnych jednostkach, najczęściej w metrach (m) lub kilometrach (km). Wyobraź sobie spacer z domu do sklepu – droga to długość tej trasy, powiedzmy 500 metrów.

Prędkość (v)

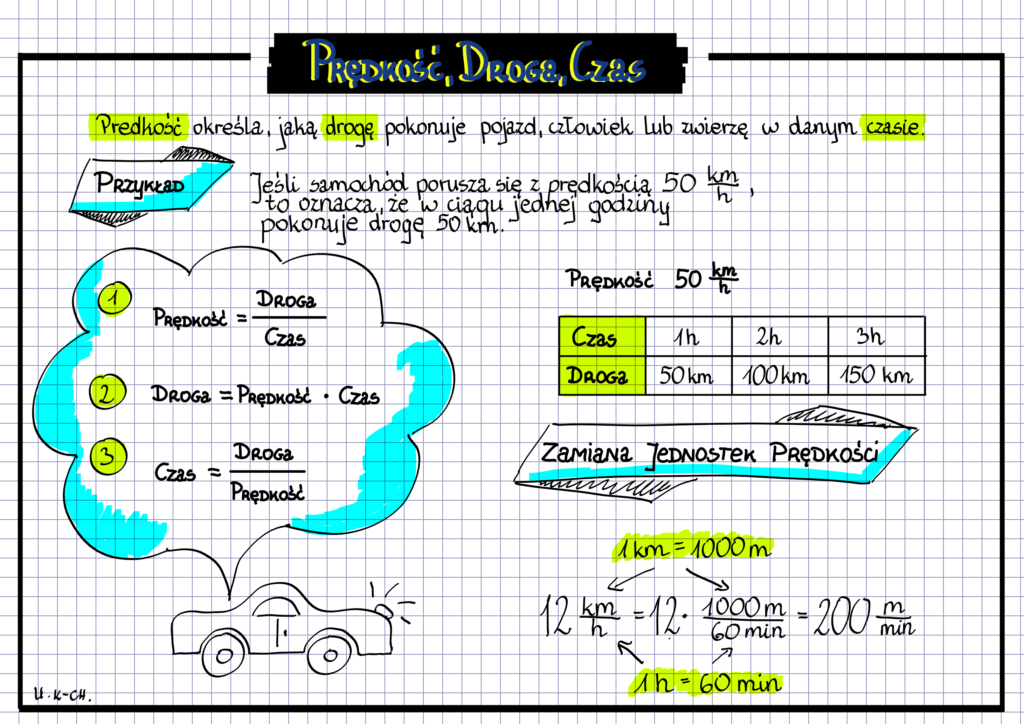
Prędkość, oznaczana literą "v" (od łacińskiego "velocitas"), to tempo, w jakim pokonujemy drogę. Mierzymy ją jako drogę podzieloną przez czas, więc najpopularniejsze jednostki to metry na sekundę (m/s) lub kilometry na godzinę (km/h). Na przykład, jeśli jedziesz samochodem z prędkością 60 km/h, to w ciągu godziny pokonasz 60 kilometrów. Warto pamiętać, że prędkość jest wektorem - ma kierunek i zwrot. Mówiąc o samej wartości, używamy określenia "szybkość".

Czas (t)

Czas, oznaczany literą "t" (od łacińskiego "tempus"), to po prostu okres, w którym coś się dzieje. Mierzymy go w sekundach (s), minutach (min) lub godzinach (h). Czas to po prostu ten moment, który upływa podczas naszego spaceru, jazdy samochodem, czy czegokolwiek innego.

Wzór na drogę, prędkość i czas: s = v * t

Teraz najważniejsze: wzór na drogę, prędkość i czas. Jest on bardzo prosty i wygląda następująco:

s = v * t

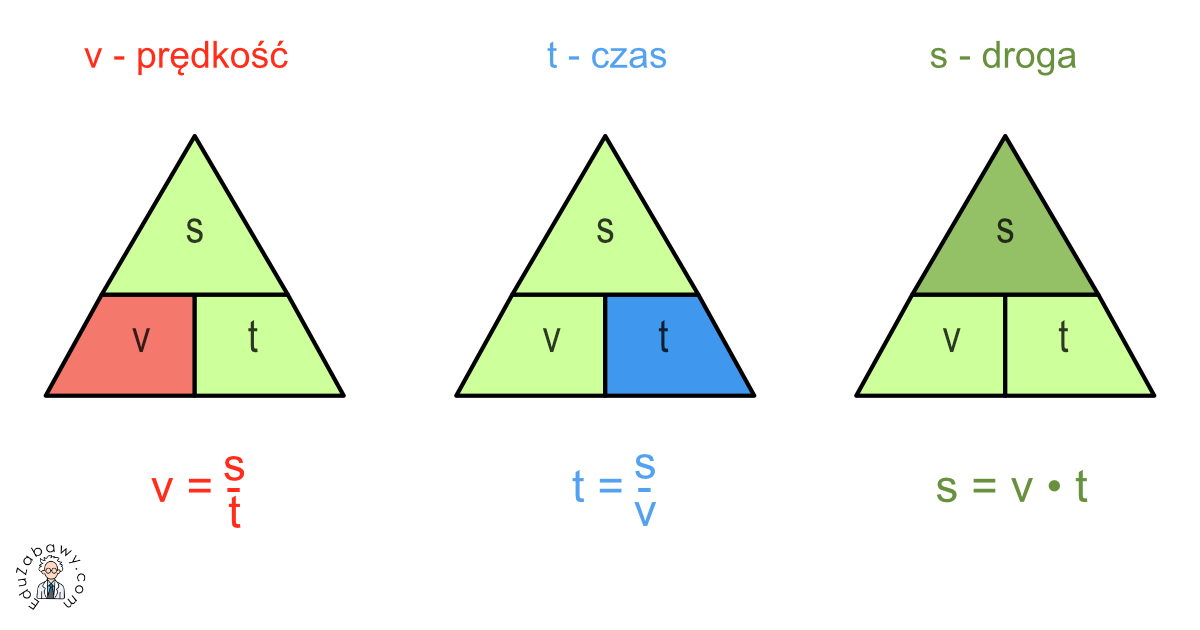
Gdzie:

s to droga
v to prędkość
t to czas

Ten wzór mówi nam, że droga, którą pokonujemy, jest równa iloczynowi prędkości i czasu. Brzmi skomplikowanie? Spójrzmy na to na przykładach.

Przykłady zastosowania wzoru

Przykład 1: Obliczanie drogi

Załóżmy, że jedziesz samochodem z prędkością 80 km/h przez 2 godziny. Jaką drogę pokonasz?

Używamy wzoru: s = v * t

s = 80 km/h * 2 h

s = 160 km

Odp: Pokonasz 160 kilometrów.

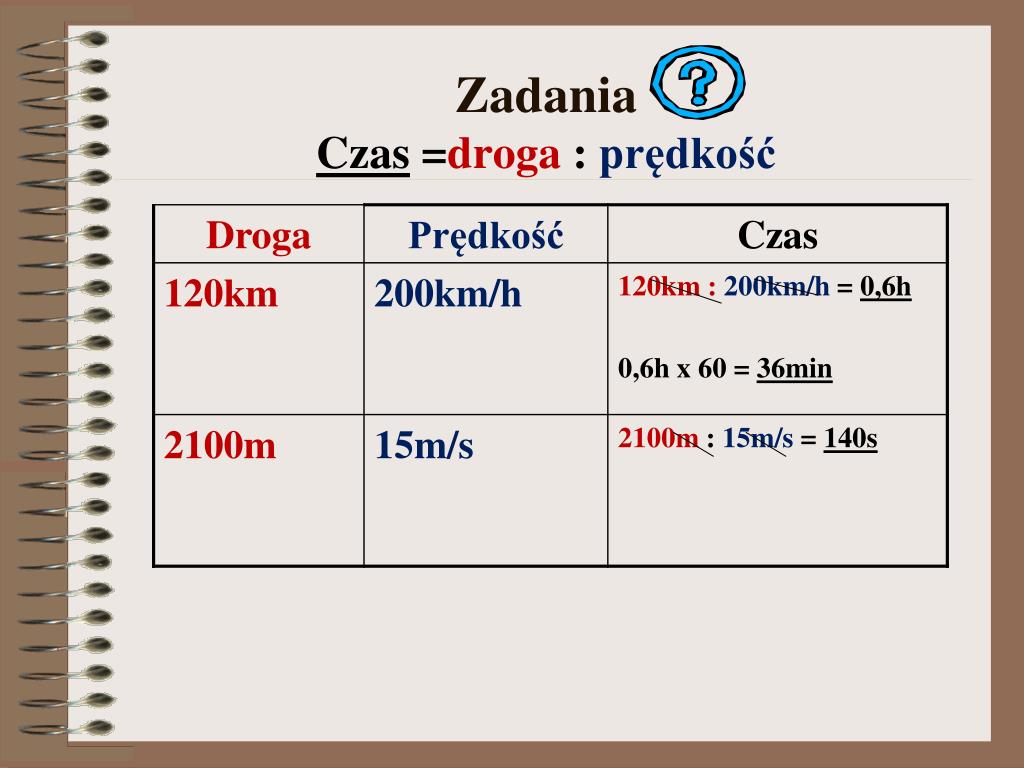
Przykład 2: Obliczanie czasu

Musisz przejechać 300 kilometrów, a jedziesz z prędkością 60 km/h. Ile czasu Ci to zajmie?

Aby obliczyć czas, musimy przekształcić wzór: t = s / v

t = 300 km / 60 km/h

t = 5 h

Odp: Zajmie Ci to 5 godzin.

Przykład 3: Obliczanie prędkości

Przebiegłeś 100 metrów w 20 sekund. Z jaką prędkością biegłeś?

Aby obliczyć prędkość, musimy przekształcić wzór: v = s / t

v = 100 m / 20 s

v = 5 m/s

Odp: Biegłeś z prędkością 5 metrów na sekundę.

Praktyczne zastosowania w życiu codziennym

Wzór na drogę, prędkość i czas ma mnóstwo praktycznych zastosowań w naszym życiu. Oto kilka przykładów:

Planowanie podróży: Obliczanie czasu dojazdu do celu, biorąc pod uwagę prędkość samochodu i odległość.
Sport: Analizowanie wyników sportowych, np. obliczanie średniej prędkości biegacza.
Logistyka: Planowanie transportu towarów, uwzględniając czas dostawy i prędkość pojazdów.
Nawigacja: Wykorzystywanie GPS do obliczania czasu dojazdu i odległości.

Wyobraź sobie, że planujesz wakacje. Chcesz dojechać nad morze, które jest oddalone o 500 km. Sprawdzasz w Internecie średnią prędkość, z jaką jeżdżą inni kierowcy na tej trasie – powiedzmy 80 km/h. Korzystając ze wzoru t = s / v, obliczasz, że podróż zajmie Ci około 6.25 godziny (500 km / 80 km/h = 6.25 h). Możesz teraz lepiej zaplanować swoje postoje i czas przyjazdu!

Ważne uwagi i pułapki

Podczas korzystania ze wzoru na drogę, prędkość i czas, warto pamiętać o kilku ważnych kwestiach:

Jednostki: Upewnij się, że używasz spójnych jednostek. Jeśli droga jest podana w kilometrach, a prędkość w metrach na sekundę, musisz zamienić jedną z tych wartości, żeby wynik był poprawny. Na przykład, aby zamienić km/h na m/s mnożymy przez 1000/3600 (czyli dzielimy przez 3.6).
Prędkość średnia a chwilowa: Wzór ten zakłada, że prędkość jest stała. W rzeczywistości prędkość często się zmienia. Otrzymany wynik to wtedy prędkość średnia.
Ruch jednostajny prostoliniowy: Wzór ten działa najlepiej w przypadku ruchu jednostajnego prostoliniowego, czyli ruchu, w którym prędkość jest stała, a tor ruchu jest linią prostą. W bardziej skomplikowanych sytuacjach, na przykład podczas ruchu zmiennego, potrzebne są bardziej zaawansowane metody obliczeń.

Przyjrzyjmy się przykładom, gdzie łatwo popełnić błąd. Załóżmy, że ktoś mówi: "Przejechałem 100 metrów w 1 minutę". Aby obliczyć prędkość w metrach na sekundę, musisz pamiętać o zamianie minut na sekundy (1 minuta = 60 sekund). Czyli v = 100 m / 60 s ≈ 1.67 m/s. Częsty błąd to pomijanie tej zamiany i liczenie v = 100 m / 1 min, co daje błędny wynik.

Podsumowanie i zachęta do dalszej nauki

Wzór na drogę, prędkość i czas (s = v * t) to potężne narzędzie, które pomaga nam zrozumieć i opisywać ruch. Znajomość tego wzoru i umiejętność jego stosowania przydaje się w wielu dziedzinach życia, od planowania podróży po analizę wyników sportowych. Pamiętaj o spójnych jednostkach i o tym, że wzór najlepiej sprawdza się w przypadku ruchu jednostajnego prostoliniowego.

Zachęcam Cię do dalszego zgłębiania wiedzy z zakresu fizyki. Wzór na drogę, prędkość i czas to dopiero początek fascynującej podróży w świat nauki. Eksperymentuj, rozwiązuj zadania i odkrywaj, jak fizyka pomaga nam zrozumieć otaczający nas świat!