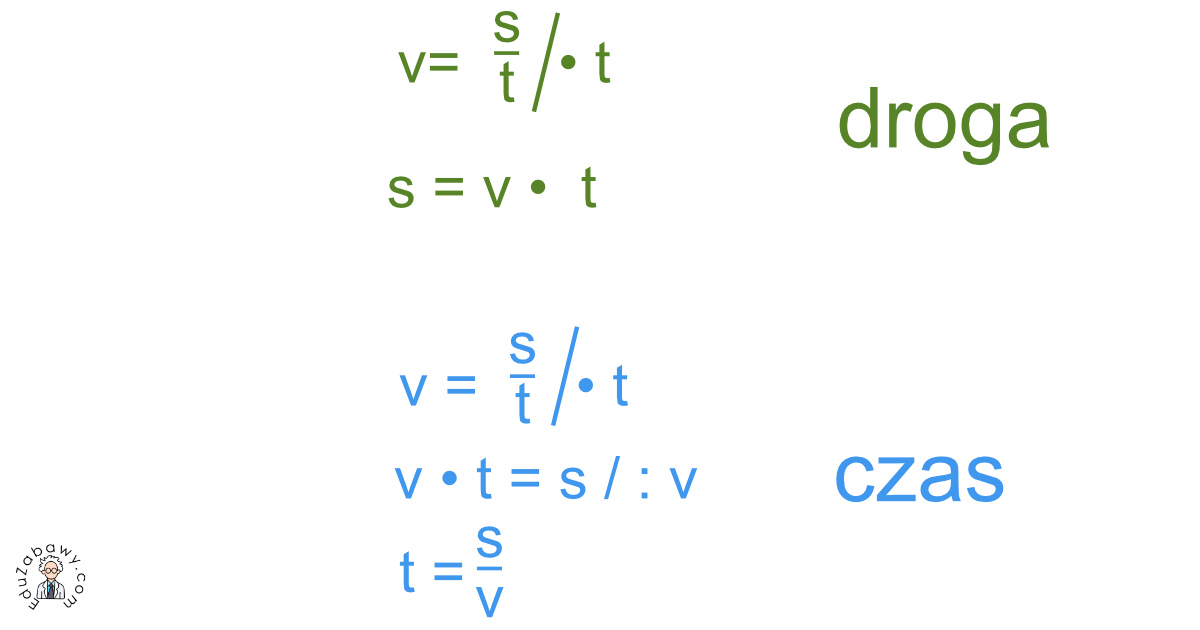Wzor Na Czas Droge I Predkosc

Czy kiedykolwiek spóźniłeś się na ważne spotkanie, bo źle obliczyłeś czas podróży? A może zastanawiałeś się, ile czasu zajmie Ci przejechanie trasy na wymarzone wakacje? Zrozumienie zależności między czasem, drogą i prędkością jest kluczowe nie tylko w życiu codziennym, ale i w wielu dziedzinach nauki i techniki. W tym artykule przyjrzymy się bliżej tym pojęciom, przedstawimy wzory, które pomogą Ci w obliczeniach, a także podpowiemy, jak wykorzystać tę wiedzę w praktyce.

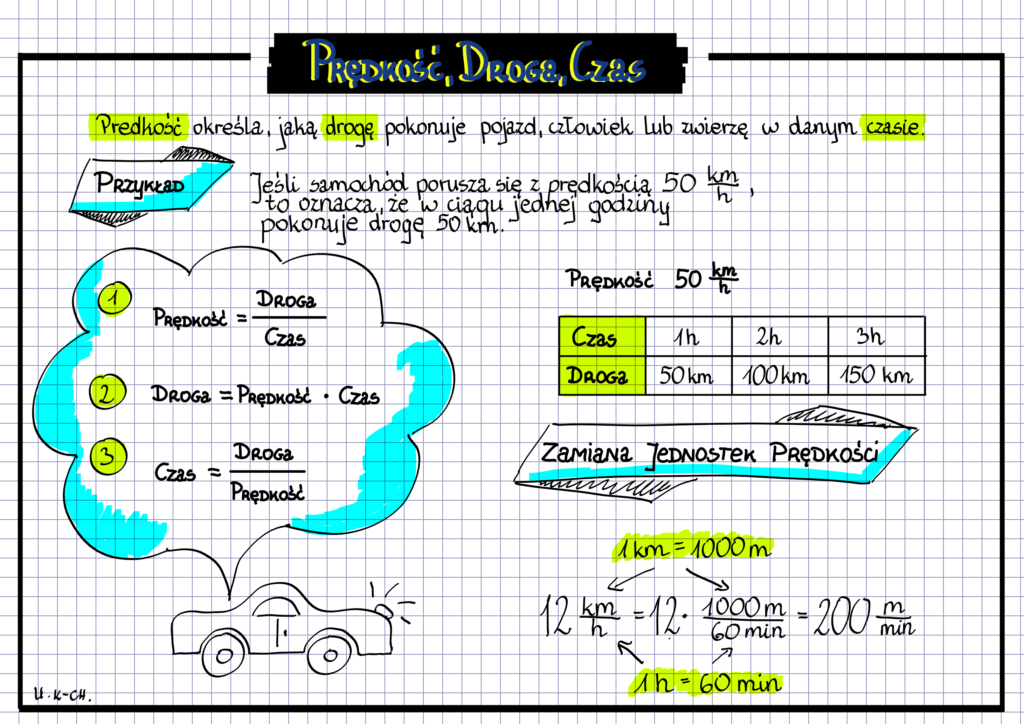
Podstawowe definicje: czas, droga, prędkość

Zanim przejdziemy do wzorów, upewnijmy się, że rozumiemy podstawowe definicje:

• Droga (s): To odległość, jaką pokonuje obiekt w ruchu. Mierzymy ją zazwyczaj w metrach (m), kilometrach (km) lub milach.
• Czas (t): To interwał, w którym odbywa się ruch. Mierzymy go w sekundach (s), minutach (min), godzinach (h) lub dniach.
• Prędkość (v): To szybkość, z jaką obiekt pokonuje drogę w danym czasie. Mierzymy ją w metrach na sekundę (m/s), kilometrach na godzinę (km/h) lub milach na godzinę (mph).

Ważne jest, aby pamiętać o jednostkach miary. Używanie niespójnych jednostek prowadzi do błędnych obliczeń. Na przykład, jeśli droga jest podana w kilometrach, a czas w minutach, należy dokonać konwersji jednostek, aby otrzymać prędkość w km/h lub m/s.

Wzory na czas, drogę i prędkość

Relacja między drogą, czasem i prędkością wyraża się prostym wzorem:

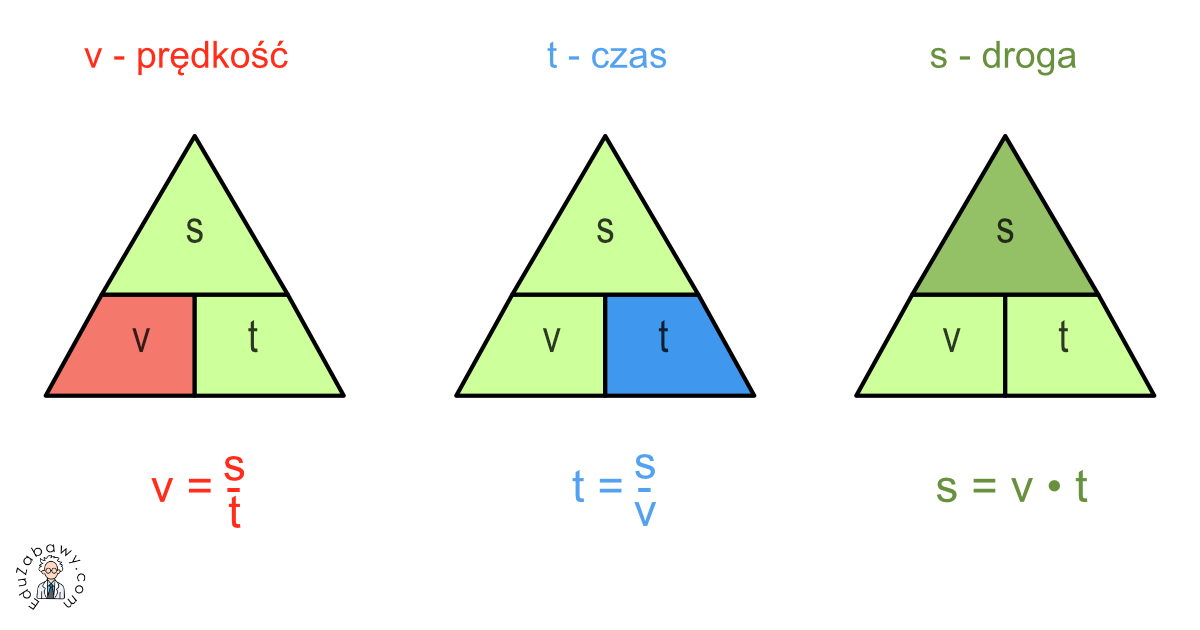
v = s / t

Prędkość równa się drodze podzielonej przez czas.

Z tego wzoru możemy wyprowadzić wzory na obliczenie drogi i czasu:

s = v * t

Droga równa się prędkości pomnożonej przez czas.

t = s / v

Czas równa się drodze podzielonej przez prędkość.

Praktyczne przykłady użycia wzorów

Spójrzmy na kilka przykładów, aby lepiej zrozumieć, jak działają te wzory:

Przykład 1: Samochód jedzie z prędkością 80 km/h przez 2 godziny. Jaką drogę pokona?

Używamy wzoru: s = v * t

s = 80 km/h * 2 h = 160 km

Odpowiedź: Samochód pokona 160 km.

Przykład 2: Rowerzysta ma do przejechania 30 km, a jedzie z prędkością 15 km/h. Ile czasu mu to zajmie?

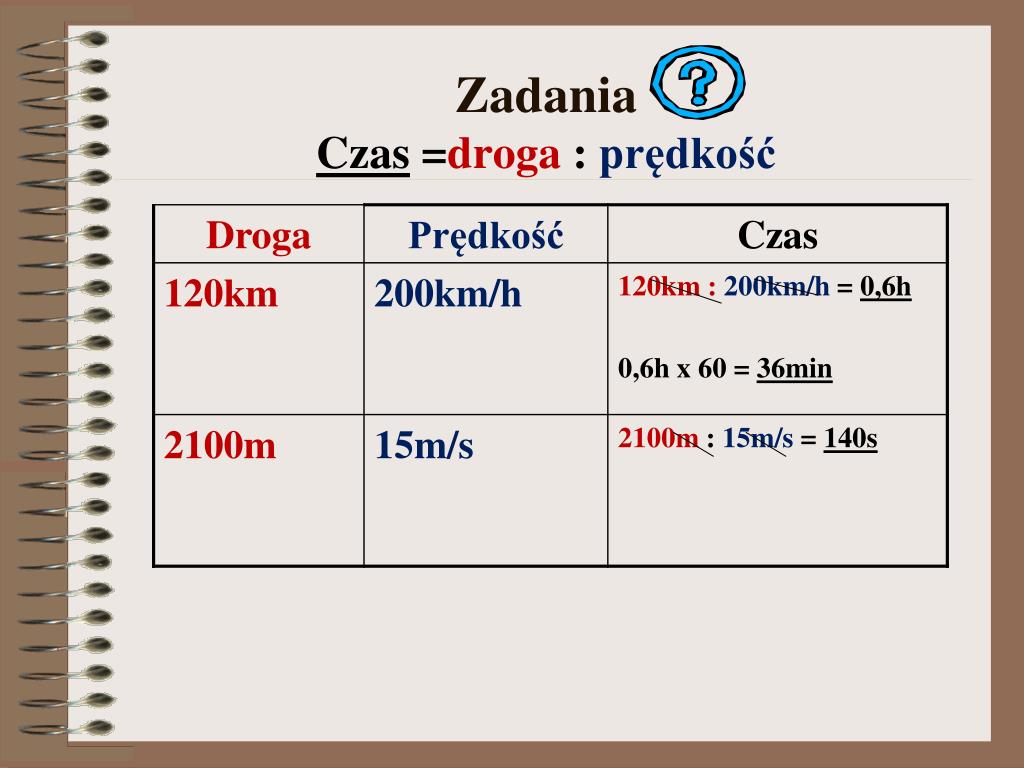
Używamy wzoru: t = s / v

t = 30 km / 15 km/h = 2 h

Odpowiedź: Rowerzyście zajmie to 2 godziny.

Przykład 3: Pociąg pokonał drogę 400 km w 4 godziny. Z jaką prędkością jechał?

Używamy wzoru: v = s / t

v = 400 km / 4 h = 100 km/h

Odpowiedź: Pociąg jechał z prędkością 100 km/h.

Zastosowania w życiu codziennym i profesjonalnym

Wiedza o zależnościach między czasem, drogą i prędkością przydaje się w wielu sytuacjach:

• Planowanie podróży: Obliczenie czasu potrzebnego na dojazd do pracy, szkoły lub na wakacje. Możesz oszacować, ile czasu zajmie Ci podróż samochodem, pociągiem, samolotem lub rowerem.
• Logistyka i transport: Firmy transportowe używają tych wzorów do optymalizacji tras i planowania dostaw, minimalizując koszty i czas transportu.
• Sport: Sportowcy i trenerzy wykorzystują te wzory do analizy wyników, planowania treningów i poprawy efektywności. Na przykład, biegacze mogą analizować swoje tempo (prędkość) na różnych odcinkach trasy.
• Nawigacja: Systemy GPS obliczają odległość do celu i szacują czas przybycia na podstawie aktualnej prędkości i warunków ruchu.
• Fizyka i inżynieria: Te podstawowe wzory są fundamentalne dla wielu obliczeń w fizyce i inżynierii, dotyczących ruchu ciał, dynamiki i kinematyki.

Problemy i pułapki w obliczeniach

Pomimo prostoty wzorów, istnieje kilka pułapek, na które należy uważać:

• Niejednolite jednostki: Upewnij się, że wszystkie wartości są wyrażone w spójnych jednostkach (np. kilometry i godziny, metry i sekundy).
• Ruch ze zmienną prędkością: Wzory działają idealnie dla ruchu ze stałą prędkością. Jeśli prędkość się zmienia, potrzebne są bardziej zaawansowane metody obliczeń, jak np. średnia prędkość.
• Opóźnienia i postoje: Planując podróż, uwzględnij dodatkowy czas na postoje, korki i inne nieprzewidziane opóźnienia.
• Zaokrąglanie wyników: Zaokrąglanie wyników pośrednich w obliczeniach może prowadzić do znacznych błędów w ostatecznym wyniku.

Średnia prędkość: Kiedy prędkość nie jest stała

W życiu codziennym rzadko mamy do czynienia z sytuacją, gdzie prędkość jest idealnie stała. Podczas podróży samochodem zwalniamy, przyspieszamy, zatrzymujemy się na światłach. W takich przypadkach możemy posłużyć się pojęciem średniej prędkości.

Średnia prędkość obliczana jest jako całkowita przebyta droga podzielona przez całkowity czas podróży:

v_śr = s_całkowita / t_całkowity

Na przykład, jeśli przejechaliśmy 200 km w 4 godziny, to nasza średnia prędkość wynosi 50 km/h, nawet jeśli w pewnych momentach jechaliśmy szybciej lub wolniej.

Zaawansowane zagadnienia

Dla bardziej zaawansowanych obliczeń, szczególnie w fizyce i inżynierii, istotne są pojęcia takie jak:

• Prędkość chwilowa: Prędkość w konkretnym momencie czasu. Można ją obliczyć, analizując bardzo małe przedziały czasu.
• Przyspieszenie: Zmiana prędkości w czasie. Oblicza się je jako zmiana prędkości podzielona przez czas, w którym ta zmiana nastąpiła.
• Ruch jednostajnie przyspieszony: Ruch, w którym prędkość zmienia się w sposób stały (przyspieszenie jest stałe). W tym przypadku używamy bardziej skomplikowanych wzorów, uwzględniających przyspieszenie.

Podsumowanie

Zrozumienie relacji między czasem, drogą i prędkością jest fundamentalne dla wielu aspektów naszego życia. Znajomość prostych wzorów pozwala nam planować podróże, analizować ruch, a nawet lepiej zrozumieć świat fizyki. Pamiętaj o spójnych jednostkach miary i uwzględnianiu ewentualnych opóźnień. Dzięki temu unikniesz niespodzianek i zawsze dotrzesz na czas!

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć wzory na czas, drogę i prędkość oraz ich praktyczne zastosowania. Teraz możesz śmiało planować swoje podróże i rozwiązywać zadania z fizyki!