Wzór Gdy Delta Jest Równa 0

Rozwiązywanie równań kwadratowych jest fundamentem wielu dziedzin matematyki i nauk pokrewnych. Jednym z kluczowych elementów w procesie rozwiązywania jest delta (Δ), zwana także wyróżnikiem równania kwadratowego. Delta pozwala nam określić liczbę i charakter rozwiązań równania. Kiedy delta przyjmuje wartość zero (Δ = 0), mamy do czynienia z szczególnym przypadkiem, który zasługuje na szczegółową analizę.

Delta i Równanie Kwadratowe – Przypomnienie

Przypomnijmy sobie, że równanie kwadratowe ma postać: ax² + bx + c = 0, gdzie a, b, i c są współczynnikami liczbowymi, a x jest niewiadomą. Współczynnik a musi być różny od zera, w przeciwnym razie równanie staje się liniowe. Delta (Δ) jest obliczana ze wzoru: Δ = b² - 4ac.

Interpretacja Wartości Delty

Wartość delty ma zasadnicze znaczenie dla liczby rozwiązań równania kwadratowego:

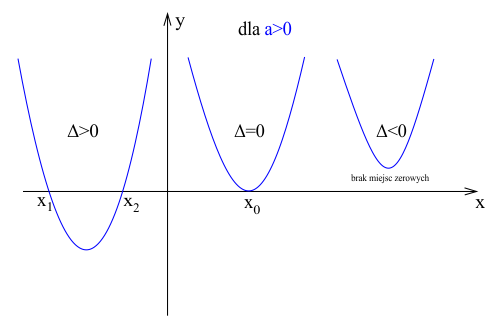
Δ > 0: Równanie ma dwa różne rozwiązania rzeczywiste.
Δ < 0: Równanie nie ma rozwiązań rzeczywistych (ma dwa rozwiązania zespolone).
Δ = 0: Równanie ma jedno rozwiązanie rzeczywiste (nazywane także rozwiązaniem podwójnym lub pierwiastkiem dwukrotnym).

Co Oznacza Delta Równa Zero?

Kiedy delta jest równa zero (Δ = 0), implikuje to, że b² - 4ac = 0. Oznacza to, że parabola reprezentująca równanie kwadratowe dotyka osi X w jednym punkcie. Inaczej mówiąc, wierzchołek paraboli leży na osi X.

Geometryczna interpretacja jest tutaj kluczowa. Wyobraźmy sobie wykres funkcji kwadratowej. Gdy delta jest dodatnia, parabola przecina oś X w dwóch miejscach. Gdy delta jest ujemna, parabola nie przecina osi X w ogóle. Natomiast, gdy delta jest równa zero, parabola styka się z osią X w jednym, jedynym punkcie – jest to wierzchołek paraboli. Ten punkt reprezentuje podwójne rozwiązanie równania.

Obliczanie Rozwiązania, Gdy Δ = 0

W przypadku gdy delta jest równa zero, możemy obliczyć rozwiązanie (x₀) korzystając ze wzoru:

x₀ = -b / 2a

Wzór ten jest uproszczeniem ogólnego wzoru na rozwiązania równania kwadratowego:

x_1,2 = (-b ± √Δ) / 2a

Gdy Δ = 0, pierwiastek z delty znika, a otrzymujemy tylko jedno rozwiązanie: x₀ = -b / 2a.

Przykłady Równań z Deltą Równą Zero

Rozważmy kilka przykładów, aby lepiej zrozumieć koncepcję.

Przykład 1

Równanie: x² + 4x + 4 = 0

Współczynniki: a = 1, b = 4, c = 4

Delta: Δ = b² - 4ac = 4² - 4 * 1 * 4 = 16 - 16 = 0

Rozwiązanie: x₀ = -b / 2a = -4 / (2 * 1) = -2

Zatem, równanie ma jedno rozwiązanie: x = -2.

Przykład 2

Równanie: 4x² - 12x + 9 = 0

Współczynniki: a = 4, b = -12, c = 9

Delta: Δ = b² - 4ac = (-12)² - 4 * 4 * 9 = 144 - 144 = 0

Rozwiązanie: x₀ = -b / 2a = -(-12) / (2 * 4) = 12 / 8 = 3/2

Zatem, równanie ma jedno rozwiązanie: x = 3/2.

Przykład 3

Równanie: 9x² + 6x + 1 = 0

Współczynniki: a = 9, b = 6, c = 1

Delta: Δ = b² - 4ac = 6² - 4 * 9 * 1 = 36 - 36 = 0

Rozwiązanie: x₀ = -b / 2a = -6 / (2 * 9) = -6 / 18 = -1/3

Zatem, równanie ma jedno rozwiązanie: x = -1/3.

Praktyczne Zastosowania Delty Równej Zero

Choć na pierwszy rzut oka może się wydawać, że równania kwadratowe z deltą równą zero są tylko ciekawostką matematyczną, w rzeczywistości mają one szereg praktycznych zastosowań. Oto kilka przykładów:

Fizyka

W fizyce, szczególnie w mechanice, delta równa zero może pojawić się podczas analizy ruchu obiektów. Na przykład, przy obliczaniu czasu, w którym obiekt osiągnie maksymalną wysokość w rzucie pionowym, możemy natknąć się na równanie kwadratowe z deltą równą zero. Rozwiązanie tego równania powie nam, kiedy obiekt osiągnie swój wierzchołek.

Inżynieria

W inżynierii, delta równa zero może pojawić się w problemach związanych z projektowaniem mostów lub budynków. Przy obliczaniu naprężeń i odkształceń, równania kwadratowe z deltą równą zero mogą pomóc w określeniu warunków, w których konstrukcja jest stabilna i nie ulegnie uszkodzeniu. Przykładowo, obliczanie optymalnego napięcia w kablu, aby zapobiec jego zerwaniu, może prowadzić do takiego równania.

Ekonomia

W ekonomii, delta równa zero może pojawić się przy modelowaniu kosztów i przychodów. Przykładowo, znalezienie punktu, w którym koszt krańcowy jest równy przychodowi krańcowemu (punkt maksymalnego zysku) może prowadzić do rozwiązania równania kwadratowego z deltą równą zero. To pozwala na zoptymalizowanie produkcji, aby uzyskać jak największy zysk przy danym poziomie kosztów.

Informatyka

W informatyce, a konkretnie w grafice komputerowej, obliczanie punktów przecięcia linii prostej z krzywą (np. okręgiem lub elipsą) może prowadzić do równania kwadratowego. Jeśli prosta jest styczna do krzywej, to delta tego równania będzie równa zero. Informacja ta jest kluczowa do tworzenia realistycznych efektów wizualnych i interakcji w grach i aplikacjach.

Podsumowanie i Wnioski

Podsumowując, delta równa zero w równaniu kwadratowym oznacza, że równanie ma jedno rozwiązanie rzeczywiste, które jest rozwiązaniem podwójnym. Geometrycznie, oznacza to, że parabola reprezentująca równanie kwadratowe dotyka osi X w jednym punkcie. Znajomość tego przypadku jest kluczowa nie tylko dla zrozumienia podstaw algebry, ale również dla rozwiązywania problemów w różnych dziedzinach nauki i techniki.

Pamiętajmy, że zrozumienie koncepcji delty i jej wpływu na rozwiązania równań kwadratowych jest fundamentem do dalszej nauki matematyki. Zachęcam do dalszego zgłębiania tematu i poszukiwania zastosowań w praktyce. Ćwiczenie rozwiązywania równań kwadratowych z różnymi wartościami delty pozwoli na lepsze zrozumienie i opanowanie tego ważnego zagadnienia.