Wzajemne Położenie Prostej I Okręgu Zadania Liceum Pdf

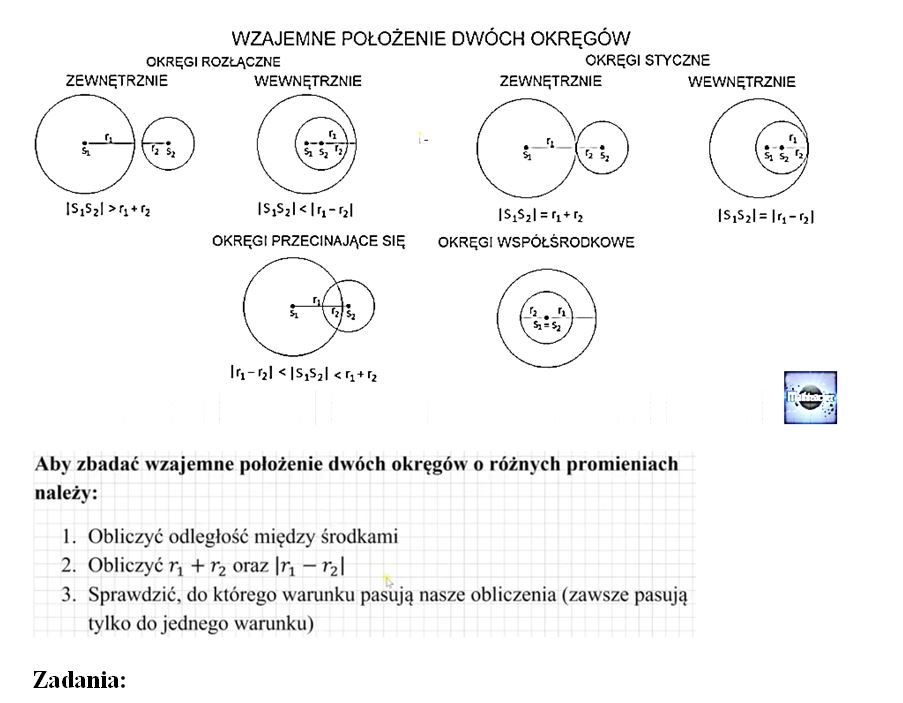
Wzajemne położenie prostej i okręgu to zagadnienie, które pojawia się w programie matematyki licealnej i jest kluczowe do zrozumienia geometrii analitycznej. Rozpatrujemy trzy podstawowe przypadki: prosta przecina okrąg w dwóch punktach (sieczna), prosta jest styczna do okręgu w jednym punkcie, oraz prosta nie przecina okręgu wcale. Każdy z tych przypadków charakteryzuje się innym zestawem własności i sposobem rozwiązywania.

Pierwszym krokiem w analizie wzajemnego położenia prostej i okręgu jest zrozumienie równań opisujących te obiekty. Okrąg o środku w punkcie S(a, b) i promieniu r można zapisać równaniem:

(x - a)² + (y - b)² = r²

Prosta natomiast najczęściej jest przedstawiana w postaci ogólnej:

Ax + By + C = 0

lub w postaci kierunkowej:

y = mx + n

gdzie m oznacza współczynnik kierunkowy, a n wyraz wolny. Wybór postaci równania prostej zależy od konkretnego zadania i tego, która forma jest wygodniejsza w danym przypadku.

Aby określić wzajemne położenie prostej i okręgu, musimy znaleźć punkty przecięcia tych dwóch figur geometrycznych. Robimy to poprzez rozwiązanie układu równań składającego się z równania okręgu i równania prostej. Najczęściej stosowaną metodą jest podstawienie. Wyrażamy jedną zmienną (np. y) z równania prostej i wstawiamy to wyrażenie do równania okręgu. Otrzymujemy wtedy równanie kwadratowe z jedną niewiadomą (x).

Rozwiązując to równanie kwadratowe, otrzymujemy dwa rozwiązania, jedno rozwiązanie lub brak rozwiązań. Liczba rozwiązań równania kwadratowego zależy od wartości wyróżnika (Δ). Przypomnijmy, że dla równania kwadratowego ax² + bx + c = 0, wyróżnik Δ obliczamy ze wzoru:

Δ = b² - 4ac

Jeżeli Δ > 0, równanie ma dwa różne rozwiązania, co oznacza, że prosta przecina okrąg w dwóch punktach (jest sieczną). Jeżeli Δ = 0, równanie ma jedno rozwiązanie (podwójne), co oznacza, że prosta jest styczna do okręgu. Jeżeli Δ < 0, równanie nie ma rozwiązań rzeczywistych, co oznacza, że prosta nie przecina okręgu.

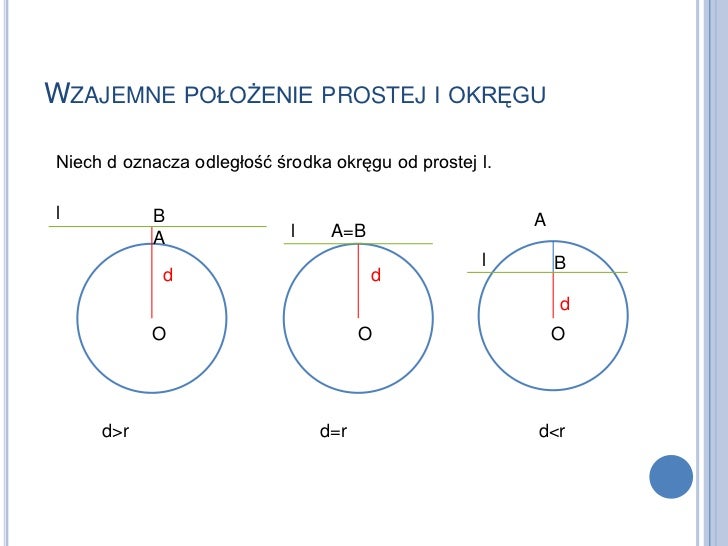
Innym sposobem analizy wzajemnego położenia prostej i okręgu jest obliczenie odległości środka okręgu od prostej. Odległość punktu S(a, b) od prostej Ax + By + C = 0 obliczamy ze wzoru:

d = |Aa + Bb + C| / √(A² + B²)

Następnie porównujemy tę odległość z promieniem okręgu. Jeżeli d < r, prosta przecina okrąg w dwóch punktach. Jeżeli d = r, prosta jest styczna do okręgu. Jeżeli d > r, prosta nie przecina okręgu.

Przykładowe Zadania

Rozważmy okrąg o równaniu (x - 2)² + (y + 1)² = 9 i prostą o równaniu y = x - 1. Chcemy określić ich wzajemne położenie.

Podstawiamy równanie prostej do równania okręgu:

(x - 2)² + (x - 1 + 1)² = 9

(x - 2)² + x² = 9

x² - 4x + 4 + x² = 9

2x² - 4x - 5 = 0

Obliczamy wyróżnik:

Δ = (-4)² - 4 * 2 * (-5) = 16 + 40 = 56

Ponieważ Δ > 0, prosta przecina okrąg w dwóch punktach.

Rozważmy okrąg o równaniu x² + y² = 4 i prostą o równaniu y = x + 2√2.

Podstawiamy równanie prostej do równania okręgu:

x² + (x + 2√2)² = 4

x² + x² + 4√2x + 8 = 4

2x² + 4√2x + 4 = 0

x² + 2√2x + 2 = 0

Obliczamy wyróżnik:

Δ = (2√2)² - 4 * 1 * 2 = 8 - 8 = 0

Ponieważ Δ = 0, prosta jest styczna do okręgu.

Rozważmy okrąg o równaniu (x + 1)² + (y - 3)² = 1 i prostą o równaniu y = x + 5.

Podstawiamy równanie prostej do równania okręgu:

(x + 1)² + (x + 5 - 3)² = 1

(x + 1)² + (x + 2)² = 1

x² + 2x + 1 + x² + 4x + 4 = 1

2x² + 6x + 4 = 0

x² + 3x + 2 = 0

Obliczamy wyróżnik:

Δ = 3² - 4 * 1 * 2 = 9 - 8 = 1

Ponieważ Δ > 0, prosta przecina okrąg w dwóch punktach.

Sprawdźmy to używając odległości środka okręgu od prostej. Środek okręgu to S(-1, 3), a równanie prostej to x - y + 5 = 0.

d = |1*(-1) - 1*3 + 5| / √(1² + (-1)²) = |-1 - 3 + 5| / √2 = 1 / √2 = √2 / 2

Promień okręgu to r = 1. Ponieważ d < r (√2 / 2 < 1), prosta przecina okrąg w dwóch punktach.

Kolejnym zadaniem może być znalezienie równania stycznej do okręgu w danym punkcie. Załóżmy, że mamy okrąg o równaniu (x - a)² + (y - b)² = r² i punkt P(x₀, y₀) leżący na tym okręgu. Wtedy prosta styczna do okręgu w punkcie P jest prostopadła do promienia okręgu łączącego środek S(a, b) z punktem P(x₀, y₀).

Współczynnik kierunkowy prostej SP wynosi:

m_SP = (y₀ - b) / (x₀ - a)

Współczynnik kierunkowy prostej stycznej jest odwrotny i przeciwny do m_SP:

m_styczna = - (x₀ - a) / (y₀ - b)

Znając współczynnik kierunkowy prostej stycznej i punkt P(x₀, y₀), możemy napisać równanie prostej stycznej w postaci:

y - y₀ = m_styczna (x - x₀)

Innym typem zadania jest znalezienie równań prostych stycznych do okręgu, przechodzących przez dany punkt leżący poza okręgiem. W tym przypadku, zakładamy, że równanie stycznej ma postać y = mx + n i wykorzystujemy warunek styczności (odległość środka okręgu od prostej równa się promieniowi okręgu). Otrzymujemy równanie z dwiema niewiadomymi (m i n), a dodatkowym warunkiem jest to, że prosta przechodzi przez dany punkt. Rozwiązując ten układ równań, otrzymujemy wartości m i n, a tym samym równania szukanych stycznych.

Podsumowując, analiza wzajemnego położenia prostej i okręgu wymaga znajomości równań tych figur geometrycznych, umiejętności rozwiązywania układów równań oraz posługiwania się pojęciem wyróżnika równania kwadratowego lub odległości punktu od prostej. Zrozumienie tych konceptów jest niezbędne do rozwiązywania bardziej zaawansowanych zadań z geometrii analitycznej.

Dalsza praktyka w rozwiązywaniu różnorodnych zadań pozwoli na lepsze zrozumienie i utrwalenie materiału. Warto eksperymentować z różnymi metodami rozwiązywania, aby znaleźć tę, która jest najbardziej efektywna w danym przypadku. Nie zapominajmy również o wizualizacji problemu, np. rysując okrąg i prostą na kartce lub używając programów do rysowania wykresów funkcji. Wizualizacja pomaga w zrozumieniu geometrycznej interpretacji problemu i w wyborze odpowiedniej metody rozwiązania.