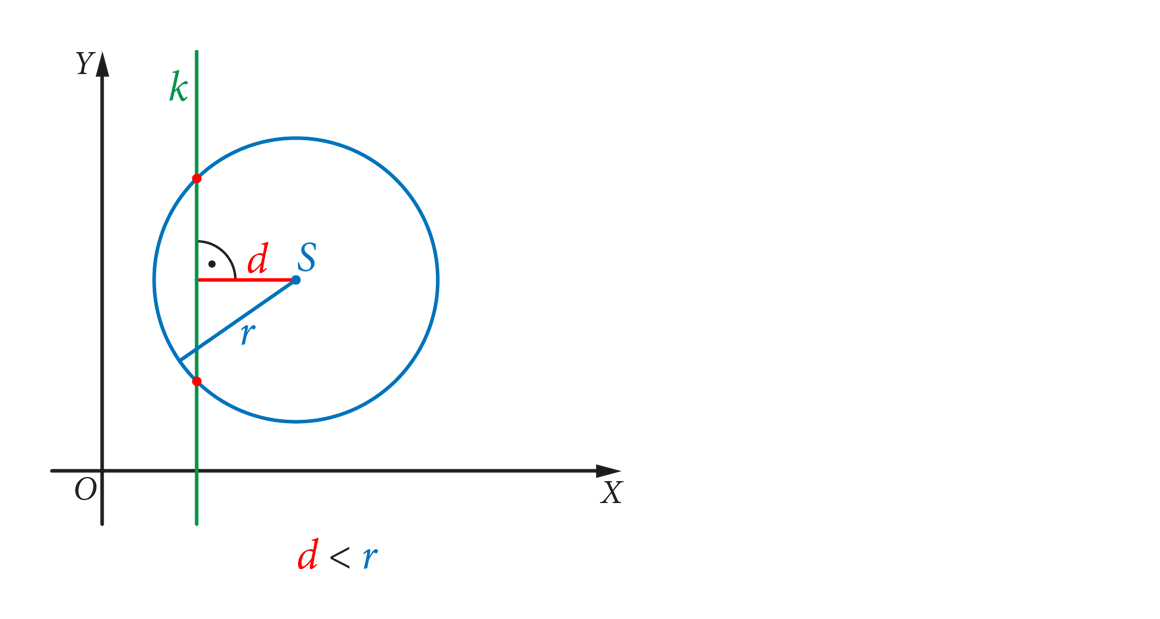Wzajemne Polozenie Okregu I Prostej

Witajcie, młodzi adepci geometrii! Dzisiaj zgłębimy fascynujący temat dotyczący relacji między okręgiem a prostą – czyli dowiemy się, w jaki sposób okrąg i prosta mogą wzajemnie się układać na płaszczyźnie. Przygotujcie się na wizualną podróż pełną porównań i prostych wyjaśnień!
Trzy Scenariusze: Dotykanie, Przecinanie i Unikanie
Wyobraźcie sobie okrąg jako pączka, a prostą jako nóż. Mamy trzy podstawowe możliwości, jak nóż może potraktować naszego pączka:
- Nóż może dotknąć pączka tylko w jednym miejscu. Wtedy prosta jest styczną do okręgu.
- Nóż może przeciąć pączka na dwie części. Wtedy prosta jest sieczną okręgu.
- Nóż może minąć pączka, nie dotykając go w ogóle. Wtedy prosta nie ma punktów wspólnych z okręgiem.
1. Prosta Styczna do Okręgu
Styczna to prosta, która ma dokładnie jeden punkt wspólny z okręgiem. Wyobraźcie sobie rowerzystę jadącego po prostej drodze, a koło roweru jako okrąg. W każdym momencie tylko jeden punkt koła dotyka ziemi (naszej prostej). Ten punkt to właśnie punkt styczności.
Kluczowa cecha stycznej: promień okręgu poprowadzony do punktu styczności jest zawsze prostopadły do stycznej. To bardzo ważne! Wyobraźcie sobie, że promień to szprycha w kole roweru, która łączy środek koła z punktem na oponie, który dotyka ziemi. Ta szprycha tworzy kąt prosty z drogą.
Przykład z życia: Dźwig podnoszący ciężar. Linka dźwigu, będąca styczną do koła pasowego, w punkcie styczności tworzy kąt prosty z promieniem koła pasowego.
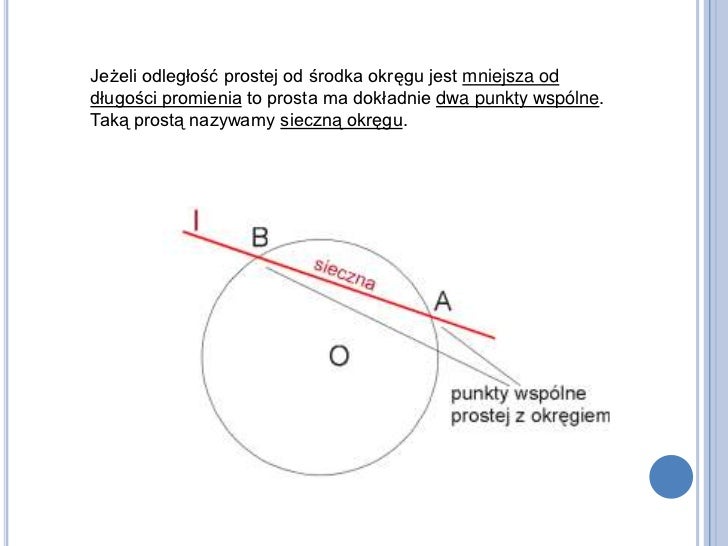
2. Prosta Sieczna Okręgu
Sieczna to prosta, która przecina okrąg w dwóch różnych punktach. Wracając do naszego pączka, to sytuacja, gdy nóż przecina pączka na dwie części. Punkty, w których prosta przecina okrąg, nazywamy punktami przecięcia.
Przykład z życia: Tor kolejowy przecinający okrągły tunel. Tory kolejowe (prosta) przecinają obwód tunelu (okrąg) w dwóch miejscach.
Ciekawostka: Odcinek siecznej zawarty wewnątrz okręgu nazywamy cięciwą okręgu. Cięciwa przechodząca przez środek okręgu jest jego średnicą.
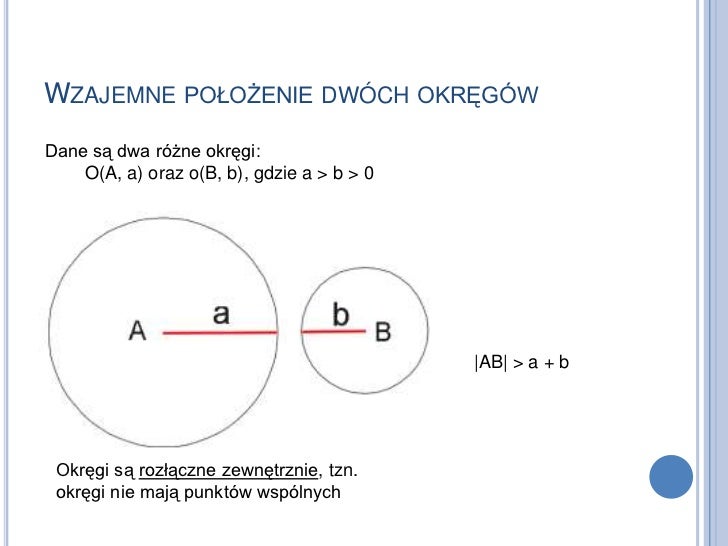
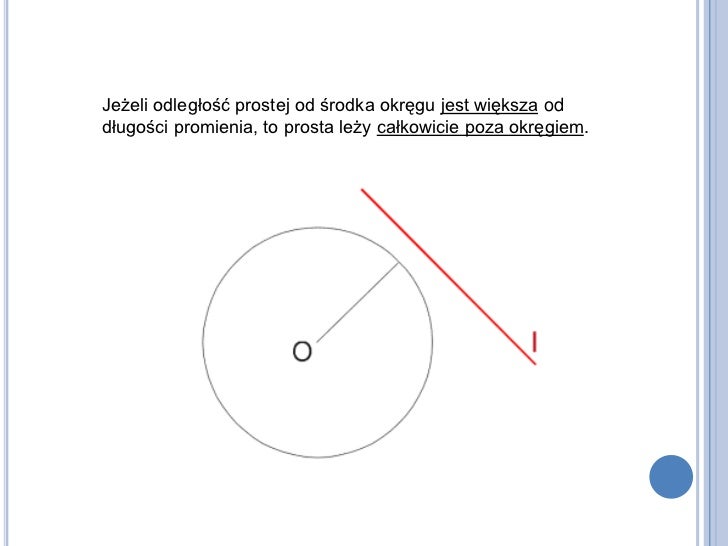
3. Prosta Nieprzecinająca Okręgu
W tym przypadku prosta i okrąg nie mają żadnych punktów wspólnych. Nóż mija pączka – nie dotyka go w ogóle. Są po prostu obok siebie, nie wchodząc ze sobą w interakcję.
Przykład z życia: Drut telefoniczny biegnący obok wieży ciśnień. Drut i wieża ciśnień (którą możemy uprościć do okręgu w pewnym widoku) nie dotykają się nawzajem.
Jak to Sprawdzić Algebraicznie?
Możemy sprawdzić, w jakim położeniu jest prosta względem okręgu, rozwiązując układ równań: równania okręgu i równania prostej.
Równanie okręgu o środku w punkcie (a, b) i promieniu r ma postać: (x - a)² + (y - b)² = r²
Równanie prostej najczęściej zapisujemy jako: y = mx + k, gdzie m to współczynnik kierunkowy, a k to wyraz wolny.
Rozwiązując układ tych równań, otrzymamy równanie kwadratowe. Liczba rozwiązań tego równania kwadratowego powie nam, w jakim położeniu jest prosta:
- Dwa rozwiązania: Prosta jest sieczną okręgu (dwa punkty przecięcia). Δ > 0
- Jedno rozwiązanie: Prosta jest styczną do okręgu (jeden punkt styczności). Δ = 0
- Brak rozwiązań: Prosta nie ma punktów wspólnych z okręgiem. Δ < 0
Pamiętaj:Δ (delta) to wyróżnik równania kwadratowego, który obliczamy ze wzoru: Δ = b² - 4ac, gdzie a, b i c to współczynniki równania kwadratowego ax² + bx + c = 0.
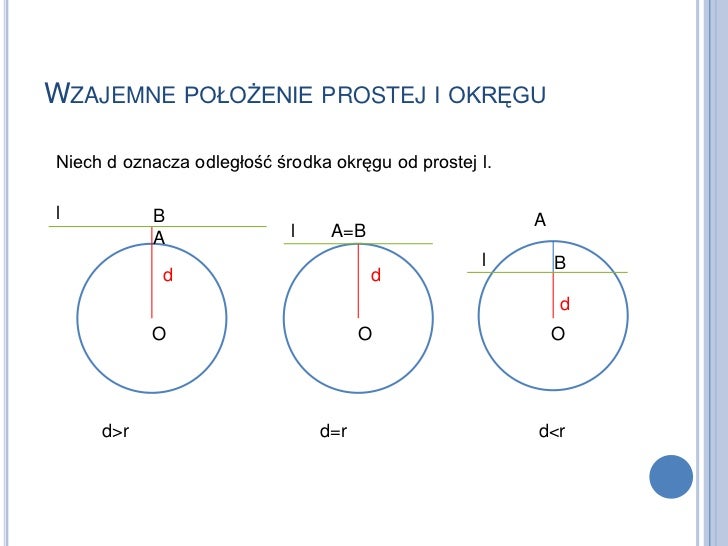
Odejmowanie Dystansu od Środka Okręgu do Prostej
Istnieje jeszcze jeden sposób na określenie wzajemnego położenia prostej i okręgu, wykorzystujący odległość od środka okręgu do prostej. Oznaczmy tę odległość jako 'd'.
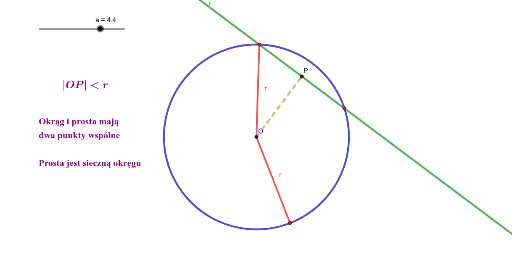
- Jeśli d < r (odległość od środka okręgu do prostej jest mniejsza niż promień), to prosta jest sieczną.
- Jeśli d = r (odległość od środka okręgu do prostej jest równa promieniowi), to prosta jest styczną.
- Jeśli d > r (odległość od środka okręgu do prostej jest większa niż promień), to prosta nie ma punktów wspólnych z okręgiem.
Wyobraźcie sobie sznur, którego jeden koniec przywiązany jest do środka okręgu, a drugi do najbliższego punktu na prostej. Długość sznura to 'd'. Porównujemy długość sznura z długością promienia. Jeśli sznur jest krótszy niż promień, to prosta musi przecinać okrąg. Jeśli mają taką samą długość, to prosta dotyka okręgu tylko w jednym punkcie. A jeśli sznur jest dłuższy, to prosta jest daleko od okręgu.
Mam nadzieję, że ta podróż po świecie okręgów i prostych była dla Was pouczająca i zrozumiała. Pamiętajcie o wizualizacjach i przykładach z życia, a geometria stanie się dla Was jeszcze bardziej fascynująca!