Wzajemne Polozenie Dwoch Okregow Zadania

W geometrii, położenie wzajemne dwóch okręgów to fascynujący temat, który kryje w sobie więcej, niż mogłoby się na pierwszy rzut oka wydawać. Analiza relacji między dwoma okręgami, ich odległości oraz promieni, pozwala na rozwiązanie wielu problemów geometrycznych i ma zastosowanie w różnych dziedzinach życia. W tym artykule przyjrzymy się bliżej temu zagadnieniu, omówimy możliwe przypadki położenia wzajemnego okręgów oraz sposoby rozwiązywania zadań z tym związanych.

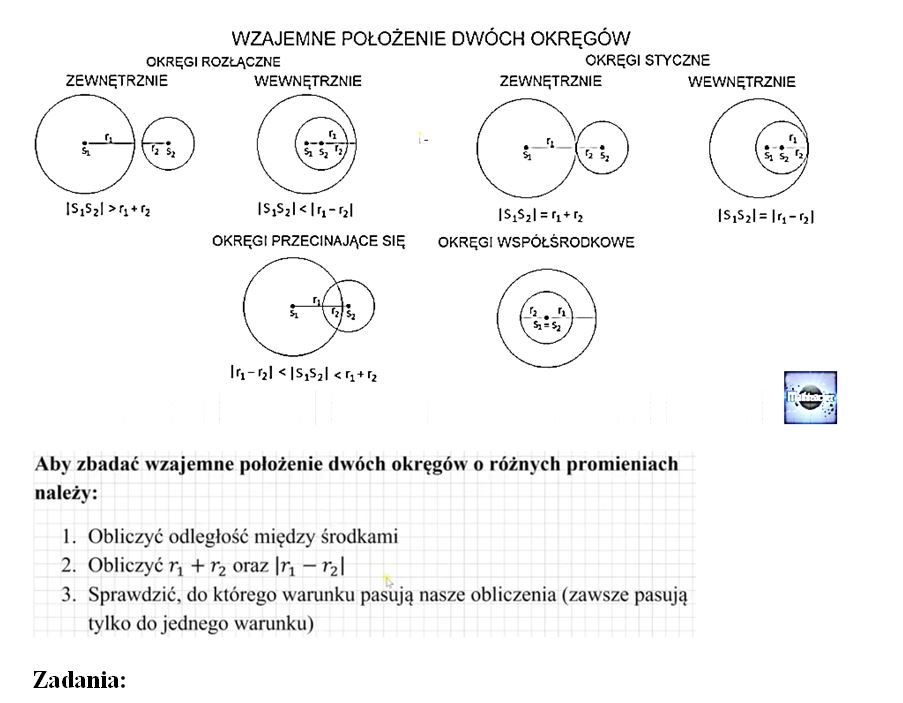
Możliwe Położenia Wzajemne Dwóch Okręgów

Dwa okręgi na płaszczyźnie mogą zajmować kilka różnych położeń względem siebie. Klasyfikacja tych położeń opiera się na analizie odległości między ich środkami (oznaczmy ją jako d) oraz wartościach ich promieni (r₁ i r₂).

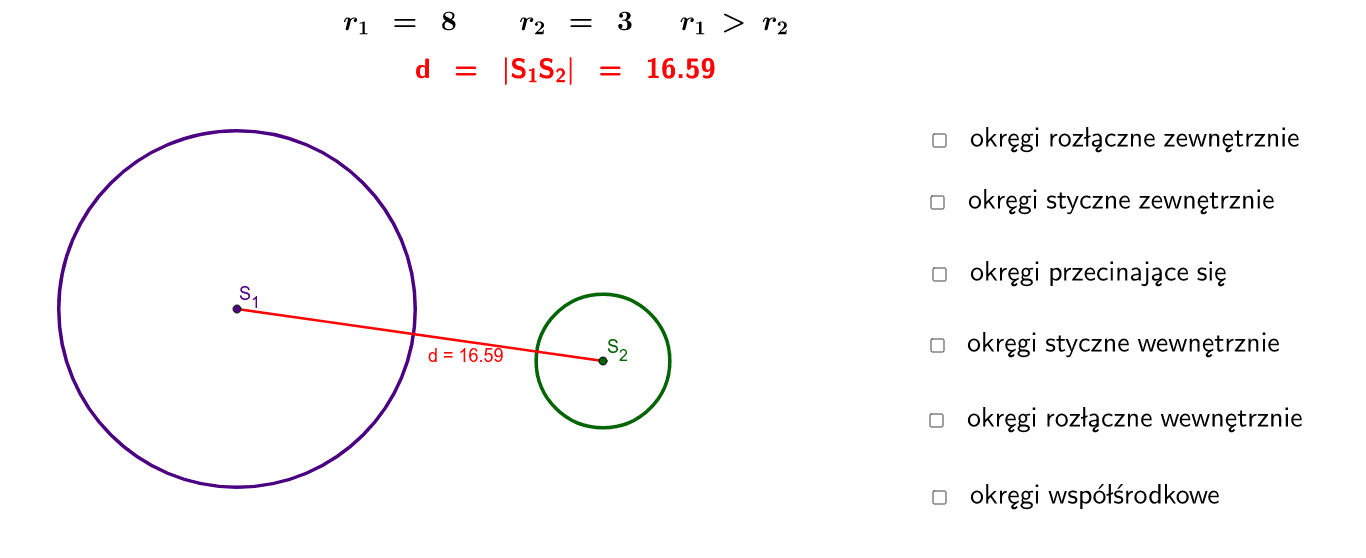
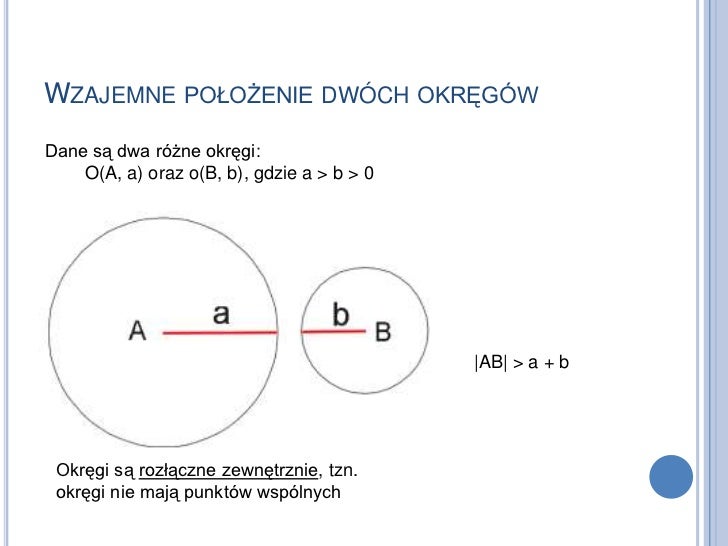
Okręgi Rozłączne Zewnętrznie

To sytuacja, w której okręgi nie mają żadnych punktów wspólnych, a jeden znajduje się na zewnątrz drugiego. Warunek, który musi być spełniony, to: d > r₁ + r₂. Oznacza to, że odległość między środkami okręgów jest większa niż suma ich promieni.

Wyobraźmy sobie dwa balony, które leżą na stole w pewnej odległości od siebie. Jeśli odległość między środkami tych balonów jest większa niż suma ich promieni, to balony się nie dotykają – mamy do czynienia z okręgami rozłącznymi zewnętrznie.

Okręgi Styczne Zewnętrznie

W tym przypadku okręgi mają dokładnie jeden punkt wspólny i jeden leży na zewnątrz drugiego. Warunek, który musi być spełniony, to: d = r₁ + r₂. Odległość między środkami okręgów jest równa sumie ich promieni.

Przykładem może być sytuacja, gdy dwa koła zębate w maszynie stykają się w jednym punkcie, przenosząc ruch obrotowy. To właśnie jest styczność zewnętrzna okręgów.

Okręgi Przecinające się

Okręgi mają dwa punkty wspólne. Warunek, który musi być spełniony, to: |r₁ - r₂| < d < r₁ + r₂. Odległość między środkami okręgów jest większa niż wartość bezwzględna różnicy ich promieni, ale mniejsza niż suma ich promieni.

Spójrzmy na dwa pierścienie olimpijskie, które się przecinają. Miejsca przecięcia pierścieni to punkty wspólne okręgów przecinających się.

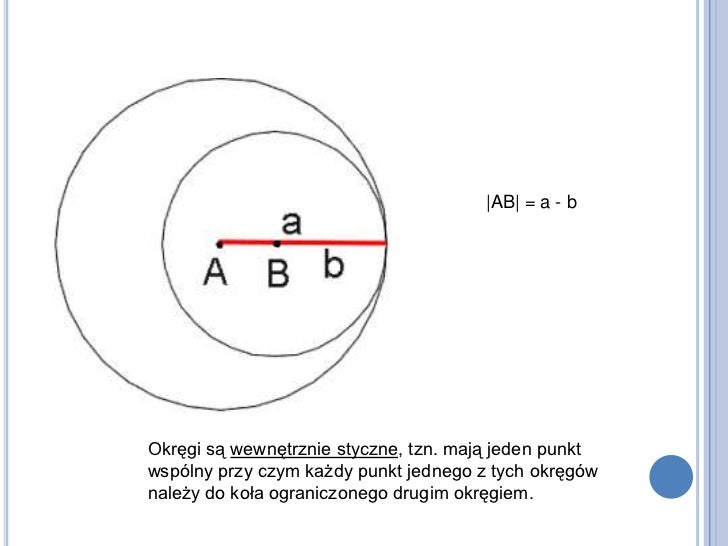
Okręgi Styczne Wewnętrznie

Okręgi mają dokładnie jeden punkt wspólny, ale jeden okrąg leży wewnątrz drugiego. Warunek, który musi być spełniony, to: d = |r₁ - r₂|. Odległość między środkami okręgów jest równa wartości bezwzględnej różnicy ich promieni.

Można to zobrazować, wyobrażając sobie kulę bilardową z wgłębieniem o kształcie okręgu, w którym idealnie pasuje mniejsza kula. Punkt styczności to właśnie styczność wewnętrzna okręgów.

Okręgi Rozłączne Wewnętrznie (Jeden Okrąg Zawiera się w Drugim)

Okręgi nie mają żadnych punktów wspólnych, a jeden okrąg leży wewnątrz drugiego. Warunek, który musi być spełniony, to: d < |r₁ - r₂|. Odległość między środkami okręgów jest mniejsza niż wartość bezwzględna różnicy ich promieni.

Przykładem może być sytuacja, gdy mamy obręcz hula-hop i w jej wnętrzu umieszczamy mniejszą obręcz, która nie dotyka ścianek zewnętrznej obręczy.

Okręgi Współśrodkowe

Szczególny przypadek, w którym środki okręgów pokrywają się. W takim przypadku d = 0. Okręgi mogą być rozłączne wewnętrznie (jeśli mają różne promienie) lub identyczne (jeśli mają takie same promienie).

Przykładem jest tarcza strzelnicza, gdzie koncentryczne okręgi są wyznaczone wokół jednego punktu centralnego.

Rozwiązywanie Zadań z Położeniem Wzajemnym Okręgów

Rozwiązywanie zadań dotyczących położenia wzajemnego okręgów często sprowadza się do wykorzystania warunków opisanych powyżej. Kluczowe jest zidentyfikowanie danych (promienie okręgów i odległość między ich środkami) i porównanie ich, aby określić, który warunek jest spełniony.

Przykład 1: Określanie Rodzaju Położenia

Dane są dwa okręgi o promieniach r₁ = 5 i r₂ = 3. Odległość między ich środkami wynosi d = 10. Określ położenie wzajemne tych okręgów.

Rozwiązanie:

• Sprawdzamy warunek dla okręgów rozłącznych zewnętrznie: d > r₁ + r₂, czyli 10 > 5 + 3, czyli 10 > 8. Warunek jest spełniony.
• Odp.: Okręgi są rozłączne zewnętrznie.

Przykład 2: Obliczanie Odległości między Środkami

Dwa okręgi o promieniach r₁ = 7 i r₂ = 2 są styczne zewnętrznie. Oblicz odległość między ich środkami.

Rozwiązanie:

• Okręgi są styczne zewnętrznie, więc d = r₁ + r₂.
• Zatem d = 7 + 2 = 9.
• Odp.: Odległość między środkami okręgów wynosi 9.

Przykład 3: Zadanie Z Geometrią Analityczną

Dany jest okrąg o równaniu (x - 2)² + (y + 1)² = 9 oraz okrąg o równaniu (x + 1)² + (y - 3)² = 4. Określ ich położenie wzajemne.

Rozwiązanie:

• Z równania pierwszego okręgu odczytujemy środek S₁ = (2, -1) i promień r₁ = 3.
• Z równania drugiego okręgu odczytujemy środek S₂ = (-1, 3) i promień r₂ = 2.
• Obliczamy odległość między środkami: d = √((2 - (-1))² + (-1 - 3)²) = √(3² + (-4)²) = √(9 + 16) = √25 = 5.
• Porównujemy d z r₁ + r₂: 5 = 3 + 2, więc d = r₁ + r₂.
• Odp.: Okręgi są styczne zewnętrznie.

Zastosowania w Realnym Świecie

Zrozumienie położenia wzajemnego okręgów ma zastosowanie w wielu dziedzinach:

Podsumowanie

Położenie wzajemne dwóch okręgów to ważne zagadnienie w geometrii, które pozwala na analizę relacji między okręgami na płaszczyźnie. Zrozumienie warunków, które muszą być spełnione, aby okręgi były rozłączne, styczne lub przecinające się, jest kluczowe do rozwiązywania zadań geometrycznych i znajdowania zastosowań w różnych dziedzinach. Zachęcam do dalszego eksplorowania tego tematu i ćwiczenia rozwiązywania zadań, aby utrwalić zdobytą wiedzę. Pamiętaj, że geometria to fascynująca dziedzina, która rozwija logiczne myślenie i umiejętność rozwiązywania problemów.