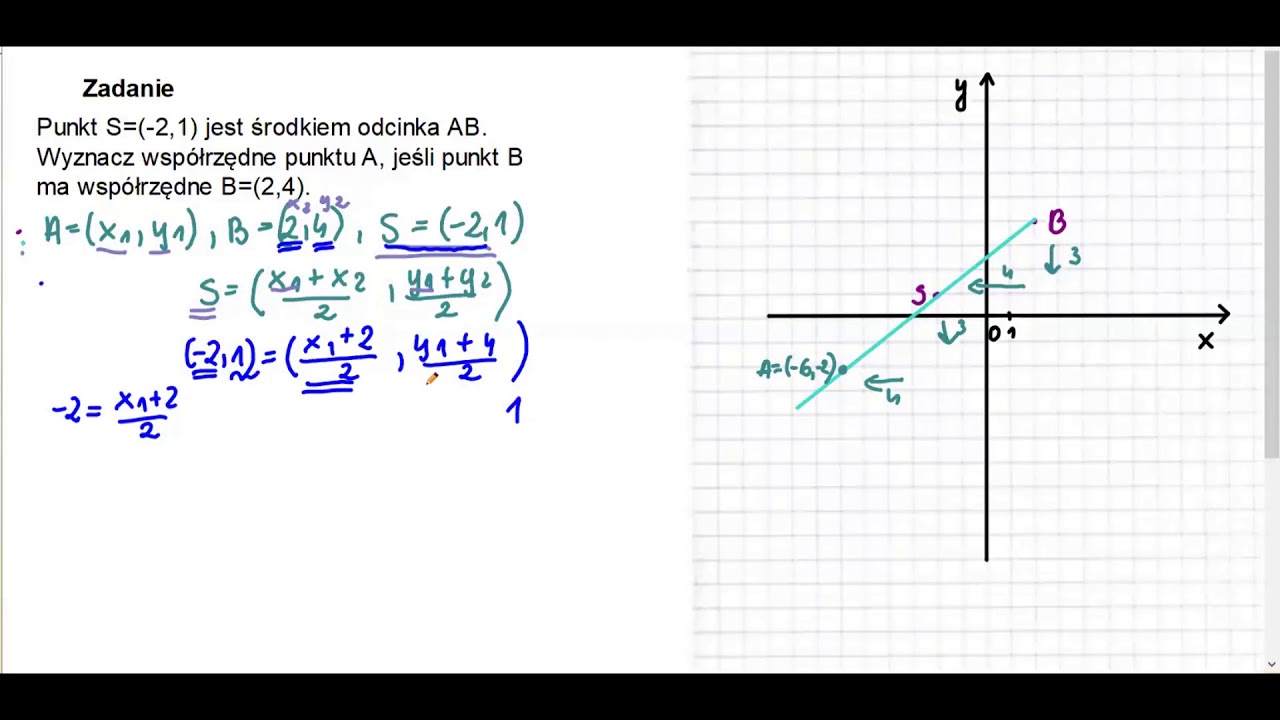
Wyznacz Współrzędne środka Odcinka Ab

Zmagasz się z problemami geometrii analitycznej? Czy obliczanie współrzędnych środka odcinka AB spędza Ci sen z powiek? Nie martw się! Wielu uczniów i studentów mierzy się z tym zagadnieniem. Kluczem jest zrozumienie prostej formuły i zastosowanie jej w praktyce. Ten artykuł krok po kroku przeprowadzi Cię przez proces obliczania współrzędnych środka odcinka, czyniąc go prostym i zrozumiałym.
Zrozumienie Podstaw: Czym Jest Środek Odcinka?
Środek odcinka to punkt, który dzieli odcinek na dwie równe części. Innymi słowy, jest to punkt leżący dokładnie w połowie drogi między dwoma punktami, które wyznaczają końce odcinka. Wyobraź sobie, że masz linijkę i odcinek narysowany na kartce. Środek odcinka to punkt, który zaznaczysz dokładnie w połowie długości tego odcinka.
W geometrii analitycznej, gdzie operujemy w układzie współrzędnych, każdy punkt jest opisany przez parę liczb: współrzędną x (odciętą) i współrzędną y (rzędną). Aby znaleźć środek odcinka w układzie współrzędnych, potrzebujemy znać współrzędne obu końców tego odcinka.
Wzór na Obliczenie Współrzędnych Środka Odcinka
Załóżmy, że mamy odcinek AB, gdzie punkt A ma współrzędne (xA, yA), a punkt B ma współrzędne (xB, yB). Wówczas współrzędne środka odcinka AB, oznaczmy go jako punkt S, możemy obliczyć za pomocą następujących wzorów:
xS = (xA + xB) / 2
yS = (yA + yB) / 2
Innymi słowy, współrzędna x środka odcinka jest średnią arytmetyczną współrzędnych x końców odcinka, a współrzędna y środka odcinka jest średnią arytmetyczną współrzędnych y końców odcinka.
To proste, prawda? Teraz przejdźmy do przykładów, aby utrwalić tę wiedzę.
Przykłady Obliczeniowe
Przykład 1: Prosty przypadek
Załóżmy, że punkt A ma współrzędne (2, 4), a punkt B ma współrzędne (6, 8). Znajdźmy współrzędne środka odcinka AB.
xS = (2 + 6) / 2 = 8 / 2 = 4
yS = (4 + 8) / 2 = 12 / 2 = 6
Zatem środek odcinka AB ma współrzędne (4, 6).
Przykład 2: Z liczbami ujemnymi
Nie bójmy się liczb ujemnych! Niech punkt A ma współrzędne (-3, 1), a punkt B ma współrzędne (5, -7). Obliczmy współrzędne środka odcinka AB.
xS = (-3 + 5) / 2 = 2 / 2 = 1
yS = (1 + (-7)) / 2 = -6 / 2 = -3
W tym przypadku środek odcinka AB ma współrzędne (1, -3).
Przykład 3: Zastosowanie w zadaniu
Odcinek AB jest średnicą okręgu. Punkt A ma współrzędne (-1, 2), a środek okręgu ma współrzędne (3, -1). Znajdź współrzędne punktu B.
W tym przypadku wiemy, że środek okręgu jest również środkiem odcinka AB. Oznaczmy współrzędne punktu B jako (xB, yB). Możemy zapisać:
3 = (-1 + xB) / 2
-1 = (2 + yB) / 2
Rozwiązując te równania, otrzymujemy:
6 = -1 + xB => xB = 7
-2 = 2 + yB => yB = -4
Zatem współrzędne punktu B to (7, -4).
Praktyczne Wskazówki i Najczęstsze Błędy
- Upewnij się, że poprawnie odczytujesz współrzędne punktów A i B. Błąd w odczytaniu nawet jednej współrzędnej zrujnuje całe obliczenia.
- Pamiętaj o kolejności działań. Najpierw dodaj współrzędne x, a następnie podziel wynik przez 2. To samo zrób dla współrzędnych y.
- Zwracaj uwagę na znaki liczb. Szczególnie przy liczbach ujemnych łatwo o pomyłkę.
- Sprawdź swój wynik. Czy obliczony punkt S leży wizualnie mniej więcej w połowie odcinka AB? Jeśli masz wątpliwości, narysuj punkty na kartce i sprawdź.
- Wykorzystuj kalkulator. Nie wstydź się używać kalkulatora, szczególnie przy bardziej skomplikowanych liczbach. Unikniesz w ten sposób błędów rachunkowych.
Dlaczego To Jest Ważne? Zastosowania w Życiu Codziennym i Nauce
Obliczanie współrzędnych środka odcinka AB nie jest tylko ćwiczeniem z matematyki. Ma ono realne zastosowania w różnych dziedzinach:
- Grafika komputerowa: Przy tworzeniu animacji, gier komputerowych i grafiki 3D, znajomość środka odcinka jest niezbędna do precyzyjnego pozycjonowania obiektów i obliczania perspektywy.
- Nawigacja: Systemy GPS często korzystają z obliczeń geometrycznych, w tym znajdowania środka odcinka, do wyznaczania optymalnych tras.
- Inżynieria: Przy projektowaniu mostów, budynków i innych konstrukcji, inżynierowie muszą precyzyjnie obliczać położenie różnych elementów, a znajomość środka odcinka może być w tym bardzo pomocna.
- Fizyka: W mechanice, środek masy ciała jest kluczowym parametrem do opisu jego ruchu. W przypadku prostych obiektów, środek masy można obliczyć wykorzystując koncepcję środka odcinka.
Ponadto, zrozumienie konceptu środka odcinka buduje solidne fundamenty dla dalszej nauki geometrii analitycznej i innych dziedzin matematyki.
Podsumowanie
Obliczanie współrzędnych środka odcinka AB jest proste, jeśli pamiętasz wzór: xS = (xA + xB) / 2 oraz yS = (yA + yB) / 2. Pamiętaj o dokładności przy odczytywaniu danych, zwracaj uwagę na znaki liczb i nie bój się używać kalkulatora. Dzięki temu bez problemu poradzisz sobie z tym zadaniem i wykorzystasz tę wiedzę w praktyce. Powodzenia!
Jeśli po przeczytaniu tego artykułu czujesz się pewniej w temacie geometrii analitycznej, to świetnie! Kontynuuj naukę i eksploruj kolejne zagadnienia. Matematyka wcale nie musi być trudna, a zrozumienie jej zasad może otworzyć przed Tobą wiele możliwości.