Wyznacz Wartosc Najmniejsza I Najwieksza W Podanym Przedziale

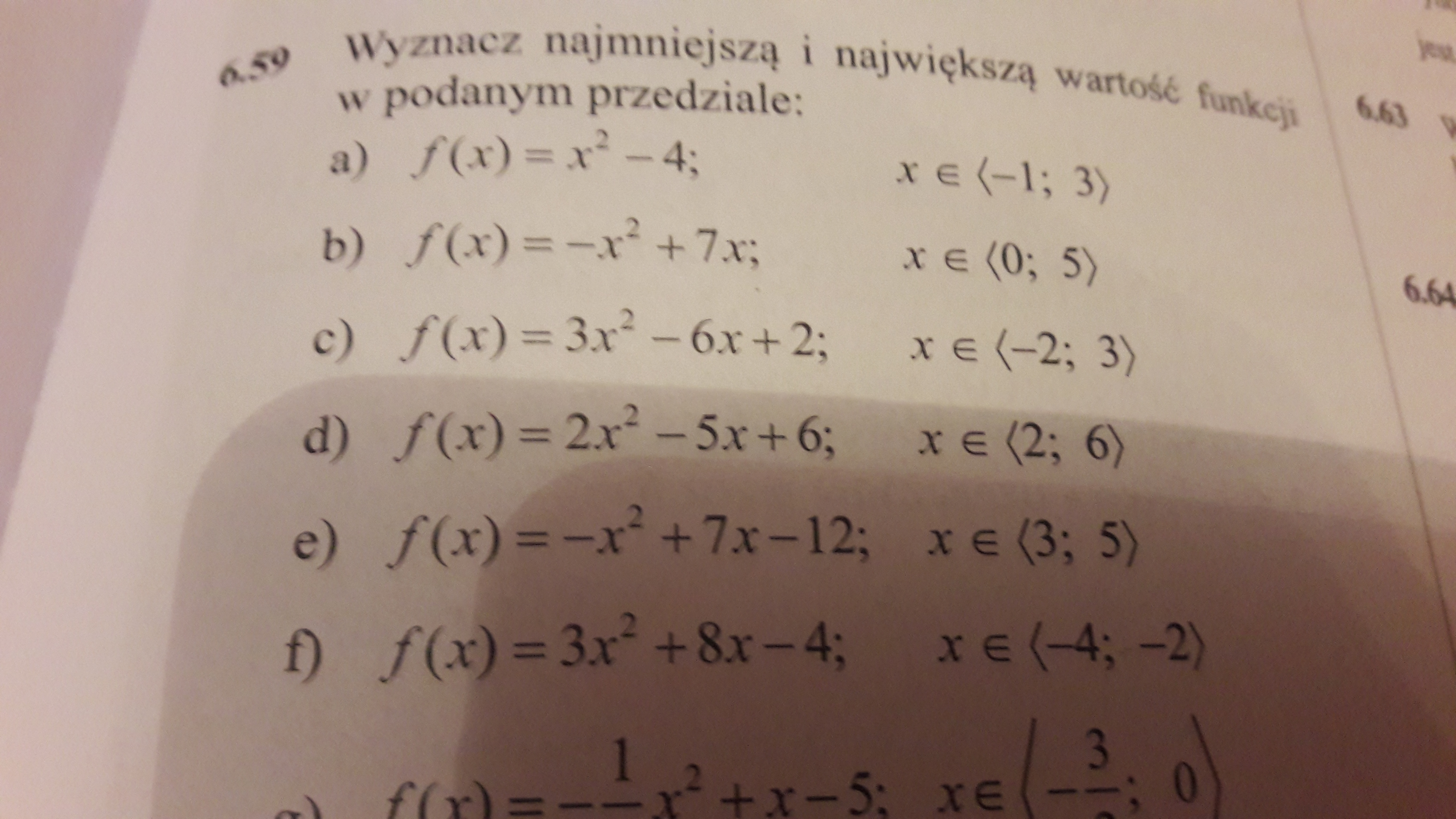
Szukanie wartości najmniejszej i największej funkcji w zadanym przedziale to kluczowe zagadnienie w analizie matematycznej, pojawiające się w wielu problemach optymalizacyjnych. Proces ten wymaga systematycznego podejścia i uwzględnienia kilku potencjalnych kandydatów na ekstremum. Przyjrzyjmy się, jak to zrobić krok po kroku.

Pierwszym krokiem jest dokładne zdefiniowanie funkcji, dla której poszukujemy ekstremów. Musimy znać wzór funkcji f(x) oraz przedział [a, b], w którym będziemy analizować jej zachowanie. Załóżmy, dla przykładu, że mamy funkcję f(x) = x³ - 6x² + 9x - 4 i interesuje nas jej zachowanie w przedziale [0, 4].

Kolejnym etapem jest obliczenie pochodnej funkcji f(x). Pochodna, oznaczana jako f'(x), informuje nas o tempie zmian funkcji. Dla naszego przykładu, pochodna funkcji f(x) = x³ - 6x² + 9x - 4 wynosi f'(x) = 3x² - 12x + 9.

Następnie szukamy punktów stacjonarnych, czyli miejsc, gdzie pochodna funkcji jest równa zero lub nie istnieje. Punkty te są potencjalnymi kandydatami na ekstrema lokalne (minimum lub maksimum). Rozwiązujemy równanie f'(x) = 0, czyli w naszym przypadku 3x² - 12x + 9 = 0. Dzieląc równanie przez 3, otrzymujemy x² - 4x + 3 = 0. Możemy to rozwiązać, znajdując pierwiastki trójmianu kwadratowego. Δ = b² - 4ac = (-4)² - 4 * 1 * 3 = 16 - 12 = 4. Zatem √Δ = 2. x₁ = (4 - 2) / 2 = 1 oraz x₂ = (4 + 2) / 2 = 3. Zatem nasze punkty stacjonarne to x = 1 oraz x = 3.

Musimy zweryfikować, czy punkty stacjonarne należą do zadanego przedziału [a, b]. Jeśli punkt stacjonarny leży poza przedziałem, ignorujemy go. W naszym przykładzie, oba punkty stacjonarne, x = 1 i x = 3, należą do przedziału [0, 4], więc bierzemy je pod uwagę.

Obliczamy wartość funkcji f(x) w punktach stacjonarnych należących do przedziału oraz na końcach przedziału, czyli w punktach a i b. Dla naszej funkcji f(x) = x³ - 6x² + 9x - 4 oraz przedziału [0, 4]:

f(0) = 0³ - 6 * 0² + 9 * 0 - 4 = -4
f(1) = 1³ - 6 * 1² + 9 * 1 - 4 = 1 - 6 + 9 - 4 = 0
f(3) = 3³ - 6 * 3² + 9 * 3 - 4 = 27 - 54 + 27 - 4 = -4
f(4) = 4³ - 6 * 4² + 9 * 4 - 4 = 64 - 96 + 36 - 4 = 0

Porównujemy wartości funkcji obliczone w poprzednim kroku. Największa wartość to wartość maksymalna funkcji w danym przedziale, a najmniejsza wartość to wartość minimalna funkcji w danym przedziale. W naszym przypadku mamy następujące wartości: -4, 0, -4, 0. Zatem wartość najmniejsza to -4, a wartość największa to 0.

Sprawdzamy, w których punktach uzyskaliśmy wartość najmniejszą i największą. W naszym przykładzie wartość najmniejszą (-4) uzyskaliśmy w punktach x = 0 oraz x = 3, a wartość największą (0) uzyskaliśmy w punktach x = 1 oraz x = 4.

Analiza Druga Pochodną

Alternatywną metodą (lub uzupełniającą) do określenia, czy punkt stacjonarny jest minimum czy maksimum lokalnym, jest wykorzystanie drugiej pochodnej funkcji. Obliczamy drugą pochodną funkcji f(x), oznaczaną jako f''(x). Dla naszej funkcji f(x) = x³ - 6x² + 9x - 4, pierwsza pochodna wynosi f'(x) = 3x² - 12x + 9, a zatem druga pochodna wynosi f''(x) = 6x - 12.

Następnie obliczamy wartość drugiej pochodnej w każdym punkcie stacjonarnym należącym do przedziału.

Jeśli f''(x) > 0, to w punkcie x mamy minimum lokalne.
Jeśli f''(x) < 0, to w punkcie x mamy maksimum lokalne.
Jeśli f''(x) = 0, test drugiej pochodnej jest nierozstrzygający i musimy zastosować inne metody (np. analizę znaku pierwszej pochodnej wokół punktu stacjonarnego).

W naszym przykładzie:

f''(1) = 6 * 1 - 12 = -6. Ponieważ f''(1) < 0, w punkcie x = 1 mamy maksimum lokalne.
f''(3) = 6 * 3 - 12 = 6. Ponieważ f''(3) > 0, w punkcie x = 3 mamy minimum lokalne.

Ta analiza potwierdza, że w punkcie x = 1 mamy do czynienia z maksimum lokalnym, a w punkcie x = 3 z minimum lokalnym. Należy jednak pamiętać, że ekstrema lokalne niekoniecznie muszą być ekstremami globalnymi (najmniejszą i największą wartością funkcji w całym przedziale). Zawsze należy porównać wartości funkcji w punktach stacjonarnych i na końcach przedziału, aby określić wartość najmniejszą i największą.

Przypadki Szczególne

Istnieją sytuacje, w których wyznaczenie wartości najmniejszej i największej funkcji może być bardziej skomplikowane. Na przykład, jeśli funkcja jest określona na przedziale otwartym (np. (a, b)), to nie ma pewności, czy funkcja osiąga wartość najmniejszą lub największą w tym przedziale. Może się zdarzyć, że funkcja zbliża się do pewnej wartości na krańcach przedziału, ale nigdy jej nie osiąga.

Kolejny przypadek to funkcje, które nie są różniczkowalne w całym przedziale. W takich przypadkach należy uwzględnić punkty, w których funkcja nie ma pochodnej (np. punkty ostre, załamania). Punkty te mogą być również kandydatami na ekstrema.

Jeśli funkcja jest kawałkami liniowa, to jej ekstrema znajdują się na końcach przedziałów, w których funkcja jest liniowa. W takim przypadku nie potrzebujemy liczyć pochodnej. Wartość funkcji w punktach łączenia się przedziałów liniowych, może być kandydatem na minimum lub maximum globalne.

Rozważmy funkcję f(x) = |x| w przedziale [-1, 2]. Ta funkcja nie jest różniczkowalna w punkcie x = 0. Musimy zatem sprawdzić wartość funkcji w punkcie x = 0 oraz na końcach przedziału:

f(-1) = |-1| = 1
f(0) = |0| = 0
f(2) = |2| = 2

Wartość najmniejsza to 0, a wartość największa to 2.

Podsumowując, wyznaczanie wartości najmniejszej i największej funkcji w zadanym przedziale wymaga dokładnej analizy funkcji, obliczenia pochodnej, znalezienia punktów stacjonarnych, sprawdzenia wartości funkcji w punktach stacjonarnych i na końcach przedziału oraz uwzględnienia przypadków szczególnych, takich jak funkcje nieróżniczkowalne. Pamiętajmy o dokładności i systematyczności w każdym kroku, aby uniknąć błędów i znaleźć poprawne rozwiązanie.