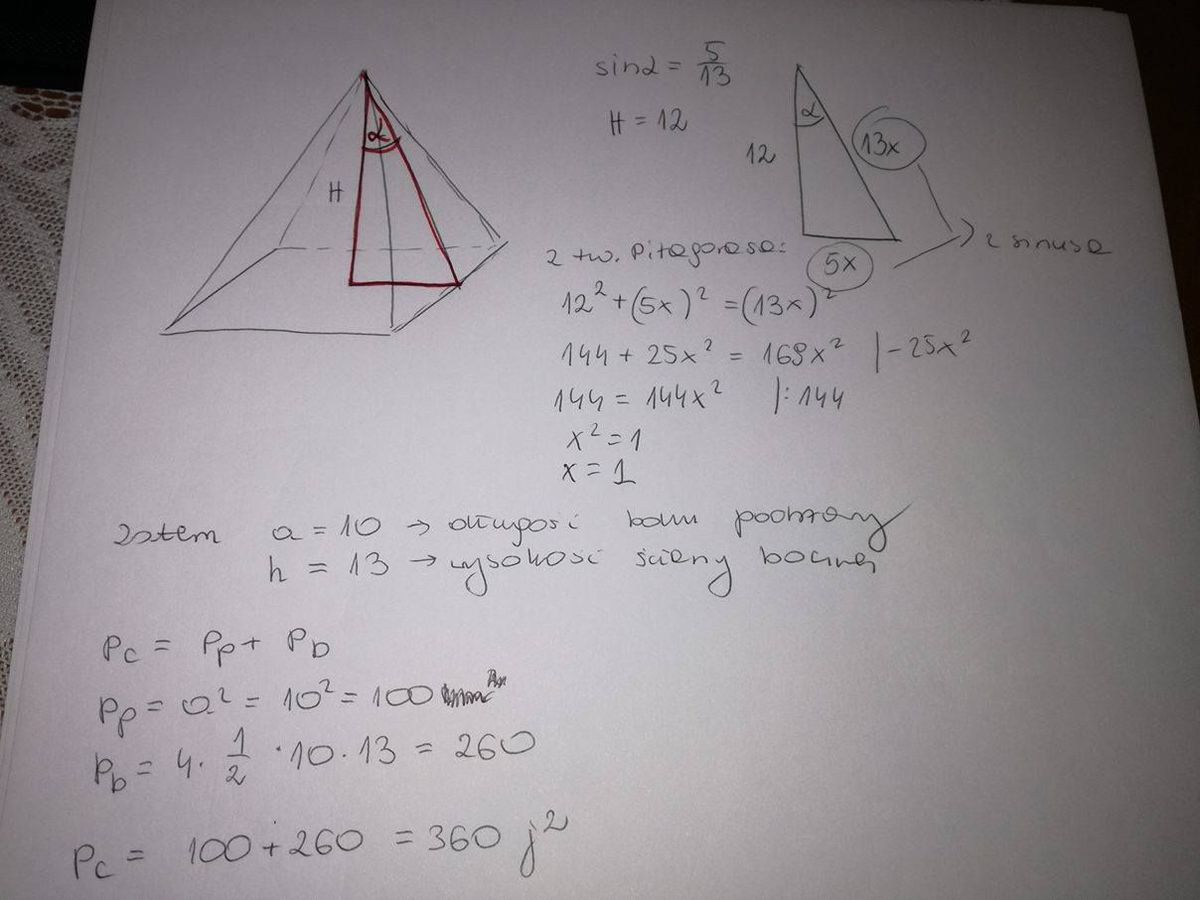
Wysokość Ostrosłupa Prawidłowego Czworokątnego Jest Równa 12

Dobrze, spróbujmy to wytłumaczyć na przykładach!

Wyobraź sobie, że masz piramidę. Ale nie taką zwykłą, losową piramidę. To jest ostrosłup prawidłowy czworokątny. Co to znaczy? Dwa ważne słowa: "prawidłowy" i "czworokątny".

"Czworokątny" mówi nam, że podstawa tej piramidy jest czworokątem, czyli figurą z czterema bokami. Najczęściej (i w zadaniach najczęściej spotykaną) jest to kwadrat.

"Prawidłowy" oznacza, że ten czworokąt jest figurą regularną, czyli wszystkie jego boki są równe, a kąty proste (czyli kwadrat). A dodatkowo, spodek wysokości ostrosłupa (punkt, w którym wysokość opada na podstawę) znajduje się dokładnie w środku tego kwadratu.

Wysokość ostrosłupa to po prostu odległość od wierzchołka ostrosłupa (tego spiczastego czubka) do podstawy, mierzona prostopadle. W naszym przypadku wiemy, że ta wysokość wynosi 12. Oznaczmy ją jako H. Czyli H = 12.

Co możemy z tym zrobić? Zazwyczaj, znając wysokość i kilka innych informacji, możemy obliczyć objętość ostrosłupa, pole powierzchni, długość krawędzi bocznej, długość krawędzi podstawy, itp. Spróbujmy przejrzeć typowe zadania.

Załóżmy, że znamy długość krawędzi podstawy! Oznaczmy ją jako a. Na przykład, niech a = 10.

Jak obliczyć objętość ostrosłupa prawidłowego czworokątnego?

Wzór na objętość ostrosłupa to:

V = (1/3) * Pole podstawy * Wysokość

W naszym przypadku:

• Pole podstawy = a² = 10² = 100
• Wysokość = H = 12

Zatem:

V = (1/3) * 100 * 12 = 400

Objętość ostrosłupa wynosi 400 jednostek sześciennych. Pamiętaj o jednostkach! Jeśli a było w centymetrach, to objętość jest w centymetrach sześciennych (cm³).

Jak obliczyć długość krawędzi bocznej?

To jest trochę bardziej skomplikowane, bo musimy skorzystać z twierdzenia Pitagorasa. Wyobraź sobie trójkąt prostokątny, którego:

• Jedna przyprostokątna to połowa długości przekątnej podstawy.
• Druga przyprostokątna to wysokość ostrosłupa (H).
• Przeciwprostokątna to krawędź boczna (oznaczmy ją jako k).

Najpierw musimy obliczyć długość przekątnej podstawy (kwadratu). Oznaczmy ją jako d. Dla kwadratu o boku a, przekątna d = a√2.

W naszym przypadku:

• a = 10
• d = 10√2

Połowa przekątnej to:

• d/2 = 5√2

Teraz możemy użyć twierdzenia Pitagorasa:

• k² = (H)² + (d/2)²
• k² = (12)² + (5√2)²
• k² = 144 + 25 * 2
• k² = 144 + 50
• k² = 194
• k = √194

Zatem długość krawędzi bocznej wynosi √194 (około 13.93).

Inny przykład:

Załóżmy teraz, że znamy pole powierzchni bocznej (P_b) i chcemy obliczyć długość krawędzi podstawy. Na przykład, niech P_b = 240.

Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego składa się z czterech identycznych trójkątów równoramiennych. Pole jednego takiego trójkąta to (1/2) * podstawa * wysokość trójkąta (wysokość ściany bocznej). Podstawa trójkąta to krawędź podstawy ostrosłupa (a). Wysokość trójkąta (ściany bocznej) oznaczmy jako h_b.

Zatem:

• P_b = 4 * (1/2) * a * h_b
• P_b = 2 * a * h_b

Wiemy, że P_b = 240, więc:

• 240 = 2 * a * h_b
• 120 = a * h_b

Nadal potrzebujemy więcej informacji! Nie wiemy ani a, ani h_b. Ale mamy H = 12. Możemy spróbować połączyć te informacje.

Wyobraźmy sobie kolejny trójkąt prostokątny, tym razem w ścianie bocznej. Jego:

• Jedna przyprostokątna to H (wysokość ostrosłupa).
• Druga przyprostokątna to połowa długości krawędzi podstawy (a/2).
• Przeciwprostokątna to h_b (wysokość ściany bocznej).

Z twierdzenia Pitagorasa:

• *h_b*² = H² + (a/2)²
• *h_b*² = 12² + (a/2)²
• *h_b*² = 144 + a²/4

Teraz mamy dwa równania:

1. 120 = a * h_b
2. *h_b*² = 144 + a²/4

Z pierwszego równania możemy wyznaczyć h_b:

• h_b = 120/a

I wstawić do drugiego równania:

• (120/a)² = 144 + a²/4
• 14400/a² = 144 + a²/4

Pomnóżmy obie strony przez 4a²:

• 57600 = 576a² + a⁴

Uporządkujmy:

• a⁴ + 576a² - 57600 = 0

To równanie kwadratowe względem a². Oznaczmy x = a².

• x² + 576x - 57600 = 0

Możemy użyć wzoru na pierwiastki równania kwadratowego:

• Δ = b² - 4ac = 576² - 4 * 1 * (-57600) = 331776 + 230400 = 562176

• √Δ = √562176 = 749.78

• x₁ = (-b + √Δ) / (2*a) = (-576 + 749.78) / 2 = 86.89

• x₂ = (-b - √Δ) / (2*a) = (-576 - 749.78) / 2 = -662.89

Ponieważ x = a², a a musi być dodatnie (długość boku), odrzucamy rozwiązanie ujemne.

Zatem:

• a² = 86.89
• a = √86.89 ≈ 9.32

W przybliżeniu, długość krawędzi podstawy wynosi 9.32.

Pamiętaj, że te obliczenia mogą stać się bardziej skomplikowane w zależności od tego, co jest dane, a co trzeba obliczyć. Kluczem jest rysowanie diagramów, identyfikowanie trójkątów prostokątnych i konsekwentne stosowanie twierdzenia Pitagorasa oraz odpowiednich wzorów. Zawsze sprawdzaj jednostki i czy wynik ma sens w kontekście zadania!