Wyrażenia Algebraiczne Zadania 8 Klasa

Czy czujesz, że wyrażenia algebraiczne w ósmej klasie to dla Ciebie czarna magia? Wiem, że dla wielu uczniów to trudny moment. Mnóstwo nowych reguł, literek zamiast liczb, i wciąż trzeba pamiętać o kolejności wykonywania działań! Ale spokojnie, ten artykuł powstał właśnie po to, żeby Ci pomóc zrozumieć, opanować i polubić tę dziedzinę matematyki. Razem przejdziemy przez najczęstsze problemy i pokażemy Ci, jak sobie z nimi radzić.

Czym właściwie są wyrażenia algebraiczne?

Wyobraź sobie, że wyrażenie algebraiczne to taki przepis kulinarny. Zamiast konkretnych składników (np. 2 jajka, 1 szklanka mąki), mamy zmienne (oznaczane literami, np. x, y, a, b) i stałe (czyli zwykłe liczby). Przepis mówi, co z tymi składnikami zrobić – jakie operacje wykonać (dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie).

Na przykład: 3x + 2y - 5 to wyrażenie algebraiczne. x i y to zmienne, 3 i 2 to współczynniki liczbowe, a -5 to stała. To cała filozofia!

Dlaczego używamy zmiennych? Dzięki zmiennym możemy zapisać ogólne zasady, które działają dla różnych wartości. Na przykład, wzór na pole prostokąta to P = a * b, gdzie a to długość jednego boku, a b to długość drugiego. Niezależnie od tego, jakie wymiary ma prostokąt, ten wzór zawsze zadziała.

Podstawowe elementy wyrażeń algebraicznych:

• Zmienne: Oznaczane literami, reprezentują nieznane wartości.
• Współczynniki liczbowe: Liczby stojące przed zmiennymi. Mnożą one zmienną.
• Stałe: Liczby, które nie zmieniają swojej wartości.
• Działania: Dodawanie (+), odejmowanie (-), mnożenie (* lub ·), dzielenie (: lub /), potęgowanie (^).

Najczęstsze problemy i jak je rozwiązać

W ósmej klasie napotkasz na kilka typowych problemów z wyrażeniami algebraicznymi. Omówmy je po kolei:

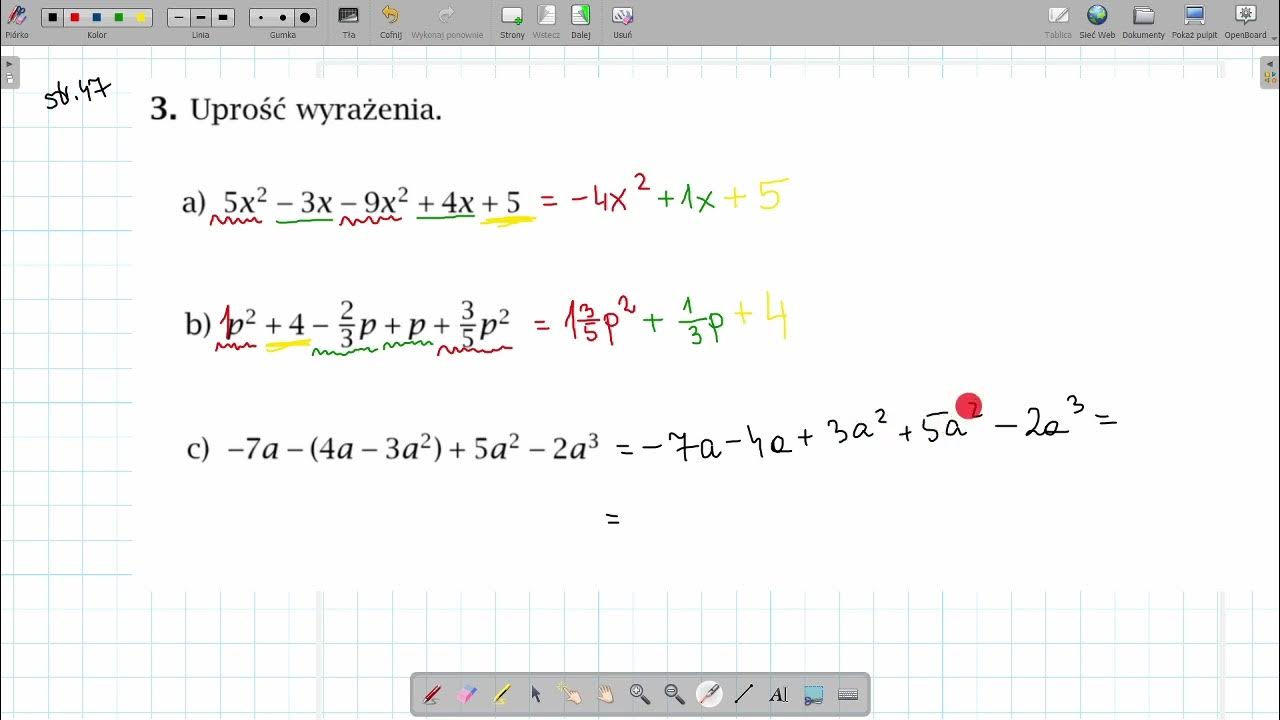
1. Upraszczanie wyrażeń algebraicznych

Upraszczanie wyrażeń to nic innego jak "posprzątanie" w przepisie. Chcemy go zapisać w jak najprostszej formie, żeby łatwiej się go używało. Robimy to, łącząc wyrazy podobne. Co to są wyrazy podobne? To takie, które mają te same zmienne w tych samych potęgach. Na przykład: 3x i -5x są wyrazami podobnymi, ale 3x i 3x² już nie.

Jak łączyć wyrazy podobne? Po prostu dodajemy lub odejmujemy ich współczynniki liczbowe. Na przykład: 3x - 5x = (3 - 5)x = -2x.

Przykład: Uprość wyrażenie: 4a + 2b - a + 5b - 3

Rozwiązanie:

1. Znajdujemy wyrazy podobne: 4a i -a oraz 2b i 5b.
2. Łączymy wyrazy podobne: (4a - a) + (2b + 5b) - 3 = 3a + 7b - 3.

2. Mnożenie sum algebraicznych

Mnożenie sum algebraicznych (czyli wyrażeń w nawiasach) to kolejny ważny temat. Trzeba pamiętać o jednej podstawowej zasadzie: każdy wyraz z jednego nawiasu mnożymy przez każdy wyraz z drugiego nawiasu.

Przykład: (x + 2)(x - 3)

Rozwiązanie:

1. Mnożymy x z pierwszego nawiasu przez x i -3 z drugiego nawiasu: x * x - x * 3 = x² - 3x.
2. Mnożymy 2 z pierwszego nawiasu przez x i -3 z drugiego nawiasu: 2 * x - 2 * 3 = 2x - 6.
3. Dodajemy otrzymane wyniki: x² - 3x + 2x - 6 = x² - x - 6.

Pamiętaj o znakach! Mnożenie plusa przez minus daje minus, a minusa przez minus daje plus.

3. Wzory skróconego mnożenia

Wzory skróconego mnożenia to taki zestaw "trików", które pozwalają szybciej mnożyć niektóre sumy algebraiczne. Warto je zapamiętać, bo bardzo ułatwiają obliczenia.

Najważniejsze wzory skróconego mnożenia:

• (a + b)² = a² + 2ab + b² (Kwadrat sumy)
• (a - b)² = a² - 2ab + b² (Kwadrat różnicy)
• (a + b)(a - b) = a² - b² (Różnica kwadratów)

Przykład: Oblicz (x + 5)², wykorzystując wzór skróconego mnożenia.

Rozwiązanie: Zastosujemy wzór na kwadrat sumy: (a + b)² = a² + 2ab + b², gdzie a = x, a b = 5.

Wstawiamy do wzoru: (x + 5)² = x² + 2 * x * 5 + 5² = x² + 10x + 25.

Widzisz, jakie to proste? Wzory skróconego mnożenia oszczędzają czas i minimalizują ryzyko pomyłek.

4. Wyłączanie wspólnego czynnika przed nawias

Wyłączanie wspólnego czynnika przed nawias to kolejna ważna umiejętność. Polega ona na znalezieniu elementu, który występuje we wszystkich składnikach wyrażenia i "wyciągnięciu" go przed nawias.

Przykład: Wyłącz wspólny czynnik przed nawias w wyrażeniu: 6x + 9y

Rozwiązanie:

1. Znajdujemy największy wspólny dzielnik współczynników liczbowych: NWD(6, 9) = 3.
2. Wyłączamy 3 przed nawias: 3(2x + 3y).

Czasami wspólnym czynnikiem może być nie tylko liczba, ale także zmienna, np. x² + 3x = x(x + 3).

Praktyczne wskazówki i triki

• Ćwicz regularnie: Matematyka to umiejętność, którą trzeba ćwiczyć. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady i nabierzesz wprawy.
• Zacznij od prostych zadań: Nie rzucaj się od razu na najtrudniejsze przykłady. Zacznij od zadań, które rozumiesz i stopniowo zwiększaj poziom trudności.
• Rozwiązuj zadania krok po kroku: Zapisuj każdy krok rozwiązania, żeby łatwiej było śledzić tok myślenia i znaleźć ewentualne błędy.
• Sprawdzaj swoje odpowiedzi: Po rozwiązaniu zadania zawsze sprawdź, czy odpowiedź jest poprawna. Możesz to zrobić, podstawiając do wyrażenia jakieś wartości za zmienne i sprawdzając, czy lewa strona równa się prawej.
• Korzystaj z zasobów online: W internecie znajdziesz mnóstwo materiałów edukacyjnych, filmów, ćwiczeń i kalkulatorów algebraicznych, które mogą Ci pomóc w nauce.
• Nie bój się pytać: Jeśli czegoś nie rozumiesz, nie krępuj się zapytać nauczyciela, rodzica, kolegi lub kogoś, kto dobrze zna matematykę. Lepiej zadać pytanie niż tkwić w niewiedzy.

Przykładowe zadania z rozwiązaniami

Zadanie 1: Uprość wyrażenie: 5x - 3y + 2x + y - 4

Rozwiązanie: (5x + 2x) + (-3y + y) - 4 = 7x - 2y - 4

Zadanie 2: Wykonaj mnożenie: (2a - 1)(a + 3)

Rozwiązanie: 2a * a + 2a * 3 - 1 * a - 1 * 3 = 2a² + 6a - a - 3 = 2a² + 5a - 3

Zadanie 3: Oblicz (3x - 2)², wykorzystując wzór skróconego mnożenia.

Rozwiązanie: (3x - 2)² = (3x)² - 2 * 3x * 2 + 2² = 9x² - 12x + 4

Zadanie 4: Wyłącz wspólny czynnik przed nawias: 12ab - 18ac

Rozwiązanie: 6a(2b - 3c)

Podsumowanie

Wyrażenia algebraiczne to fundament algebry i ważny element matematyki w ósmej klasie. Choć na początku mogą wydawać się trudne, z odpowiednim podejściem i regularną praktyką, na pewno je opanujesz. Pamiętaj o upraszczaniu wyrażeń, mnożeniu sum algebraicznych, wzorach skróconego mnożenia i wyłączaniu wspólnego czynnika przed nawias. Ćwicz regularnie, rozwiązuj zadania krok po kroku i nie bój się pytać, a sukces masz gwarantowany! Pamiętaj, jak mówił Albert Einstein:

"Nie martw się o swoje trudności z matematyką. Mogę cię zapewnić, że moje są jeszcze większe."