Wyrażenia Algebraiczne I Równania Klasa 8 Sprawdzian

Wyrażenia algebraiczne i równania to fundament algebry, a ich zrozumienie w klasie 8 jest kluczowe dla dalszej nauki matematyki. Sprawdzian z tego materiału sprawdza nie tylko umiejętność przekształcania wyrażeń, ale także zdolność rozwiązywania równań różnego typu i zastosowania tej wiedzy w praktycznych problemach. Przyjrzyjmy się bliżej zagadnieniom, które najczęściej pojawiają się na sprawdzianach z tego działu.
Pierwszym krokiem jest opanowanie podstawowych definicji i pojęć. Wyrażenie algebraiczne to połączenie liczb, zmiennych (oznaczanych zazwyczaj literami, np. x, y, a, b) i działań matematycznych (dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie). Przykładem wyrażenia algebraicznego może być: 3x + 2y - 5. Ważne jest, by umieć rozróżniać współczynniki (liczby stojące przed zmiennymi, np. 3 i 2 w powyższym przykładzie) od wyrazów wolnych (liczby bez zmiennych, np. -5).
Upraszczanie wyrażeń algebraicznych to umiejętność łączenia wyrazów podobnych, czyli tych, które mają identyczne zmienne podniesione do tych samych potęg. Na przykład, w wyrażeniu 5x + 3y - 2x + y, możemy połączyć 5x i -2x, co da nam 3x, oraz 3y i y, co da nam 4y. Ostatecznie uproszczone wyrażenie to 3x + 4y. Należy pamiętać o znakach przy łączeniu wyrazów.
Kolejnym ważnym zagadnieniem jest redukcja wyrazów podobnych w bardziej złożonych wyrażeniach. Często wymaga to zastosowania praw działań, takich jak rozdzielność mnożenia względem dodawania i odejmowania. Na przykład, aby uprościć wyrażenie 2(x + 3) - 4x + 1, najpierw mnożymy 2 przez każdy wyraz w nawiasie: 2x + 6 - 4x + 1. Następnie łączymy wyrazy podobne: 2x - 4x = -2x oraz 6 + 1 = 7. Ostatecznie uproszczone wyrażenie to -2x + 7.
Równie istotne jest usuwanie nawiasów. Należy pamiętać o zasadach dotyczących znaku minus przed nawiasem. Jeżeli przed nawiasem znajduje się znak minus, to opuszczając nawias, zmieniamy znak każdego wyrazu w nawiasie na przeciwny. Na przykład, - (2x - 3y + 1) staje się -2x + 3y - 1. Jeżeli przed nawiasem znajduje się znak plus, to opuszczamy nawias bez zmiany znaków.
Mnożenie sum algebraicznych jest kolejnym zagadnieniem, które pojawia się na sprawdzianach. Należy pomnożyć każdy wyraz w jednym nawiasie przez każdy wyraz w drugim nawiasie. Na przykład, aby pomnożyć (x + 2)(y - 3), wykonujemy następujące działania: x * y = xy, x * -3 = -3x, 2 * y = 2y, 2 * -3 = -6. Ostatecznie otrzymujemy xy - 3x + 2y - 6.
Równania i ich rozwiązywanie
Równanie to stwierdzenie równości dwóch wyrażeń algebraicznych. Rozwiązaniem równania jest taka wartość zmiennej, która po podstawieniu do równania sprawia, że lewa strona równania jest równa prawej stronie. Rozwiązywanie równań polega na przekształcaniu równania w taki sposób, aby po jednej stronie równania pozostała zmienna, a po drugiej stronie liczba.
Najprostsze równania to równania liniowe z jedną niewiadomą. Rozwiązuje się je poprzez dodawanie lub odejmowanie tej samej liczby od obu stron równania, a następnie dzielenie lub mnożenie obu stron równania przez tę samą liczbę (różną od zera). Na przykład, aby rozwiązać równanie 2x + 3 = 7, najpierw odejmujemy 3 od obu stron: 2x = 4. Następnie dzielimy obie strony przez 2: x = 2.
Bardziej skomplikowane równania mogą zawierać nawiasy i ułamki. W takim przypadku najpierw usuwamy nawiasy, a następnie pozbywamy się ułamków, mnożąc obie strony równania przez wspólny mianownik. Na przykład, aby rozwiązać równanie (x + 1)/2 = 3, mnożymy obie strony przez 2: x + 1 = 6. Następnie odejmujemy 1 od obu stron: x = 5.
Równania mogą mieć jedno rozwiązanie, nieskończenie wiele rozwiązań (tożsamość) lub nie mieć rozwiązań (sprzeczność). Na przykład, równanie x + 1 = x + 1 ma nieskończenie wiele rozwiązań, ponieważ niezależnie od wartości x, lewa strona równania zawsze będzie równa prawej stronie. Z kolei równanie x + 1 = x + 2 nie ma rozwiązań, ponieważ nie istnieje taka wartość x, która sprawiłaby, że lewa strona równania byłaby równa prawej stronie.
Sprawdzanie rozwiązań równań jest bardzo ważne. Po znalezieniu rozwiązania należy podstawić je do równania i sprawdzić, czy lewa strona równania jest równa prawej stronie. Jeżeli tak, to znalezione rozwiązanie jest poprawne. Jeżeli nie, to popełniliśmy błąd podczas rozwiązywania równania i należy poszukać błędu.
Zadania tekstowe wymagają przełożenia treści zadania na język matematyczny, czyli utworzenia równania, które opisuje sytuację przedstawioną w zadaniu. Następnie należy rozwiązać utworzone równanie i zinterpretować wynik w kontekście zadania. Na przykład: "Jacek ma o 5 lat więcej niż Kasia. Razem mają 25 lat. Ile lat ma Jacek, a ile Kasia?". Oznaczamy wiek Kasi jako x. Wtedy wiek Jacka to x + 5. Suma ich lat to x + (x + 5) = 25. Upraszczamy równanie: 2x + 5 = 25. Odejmujemy 5 od obu stron: 2x = 20. Dzielimy obie strony przez 2: x = 10. Zatem Kasia ma 10 lat, a Jacek 10 + 5 = 15 lat.
Oprócz równań liniowych, w klasie 8 uczniowie mogą spotkać się z równaniami, w których niewiadoma występuje w mianowniku. Rozwiązując takie równania, należy najpierw pomnożyć obie strony równania przez mianownik, aby pozbyć się ułamka. Należy jednak pamiętać o określeniu dziedziny równania, czyli wykluczeniu wartości niewiadomej, dla których mianownik jest równy zero. Na przykład, w równaniu 1/(x - 2) = 3, dziedziną jest x ≠ 2. Mnożymy obie strony przez (x - 2): 1 = 3(x - 2). Upraszczamy: 1 = 3x - 6. Dodajemy 6 do obu stron: 7 = 3x. Dzielimy obie strony przez 3: x = 7/3. Ponieważ 7/3 należy do dziedziny, jest to poprawne rozwiązanie.
Nierówności to kolejne zagadnienie, które może pojawić się na sprawdzianie. Nierówność to stwierdzenie, że jedno wyrażenie algebraiczne jest większe, mniejsze, większe lub równe, lub mniejsze lub równe od drugiego wyrażenia algebraicznego. Rozwiązywanie nierówności jest bardzo podobne do rozwiązywania równań, z jednym ważnym wyjątkiem: mnożąc lub dzieląc obie strony nierówności przez liczbę ujemną, należy zmienić znak nierówności na przeciwny. Na przykład, aby rozwiązać nierówność -2x > 4, dzielimy obie strony przez -2, pamiętając o zmianie znaku nierówności: x < -2. Rozwiązaniem nierówności jest zbiór wszystkich liczb mniejszych od -2.
Podsumowując, sprawdzian z wyrażeń algebraicznych i równań w klasie 8 wymaga solidnej wiedzy z zakresu upraszczania wyrażeń, rozwiązywania równań liniowych i nierówności, a także umiejętności stosowania tej wiedzy w praktycznych zadaniach tekstowych. Kluczem do sukcesu jest systematyczna praca, rozwiązywanie dużej liczby zadań i sprawdzanie swoich rozwiązań. Ważne jest również zrozumienie podstawowych definicji i pojęć, aby móc skutecznie radzić sobie z bardziej skomplikowanymi problemami.




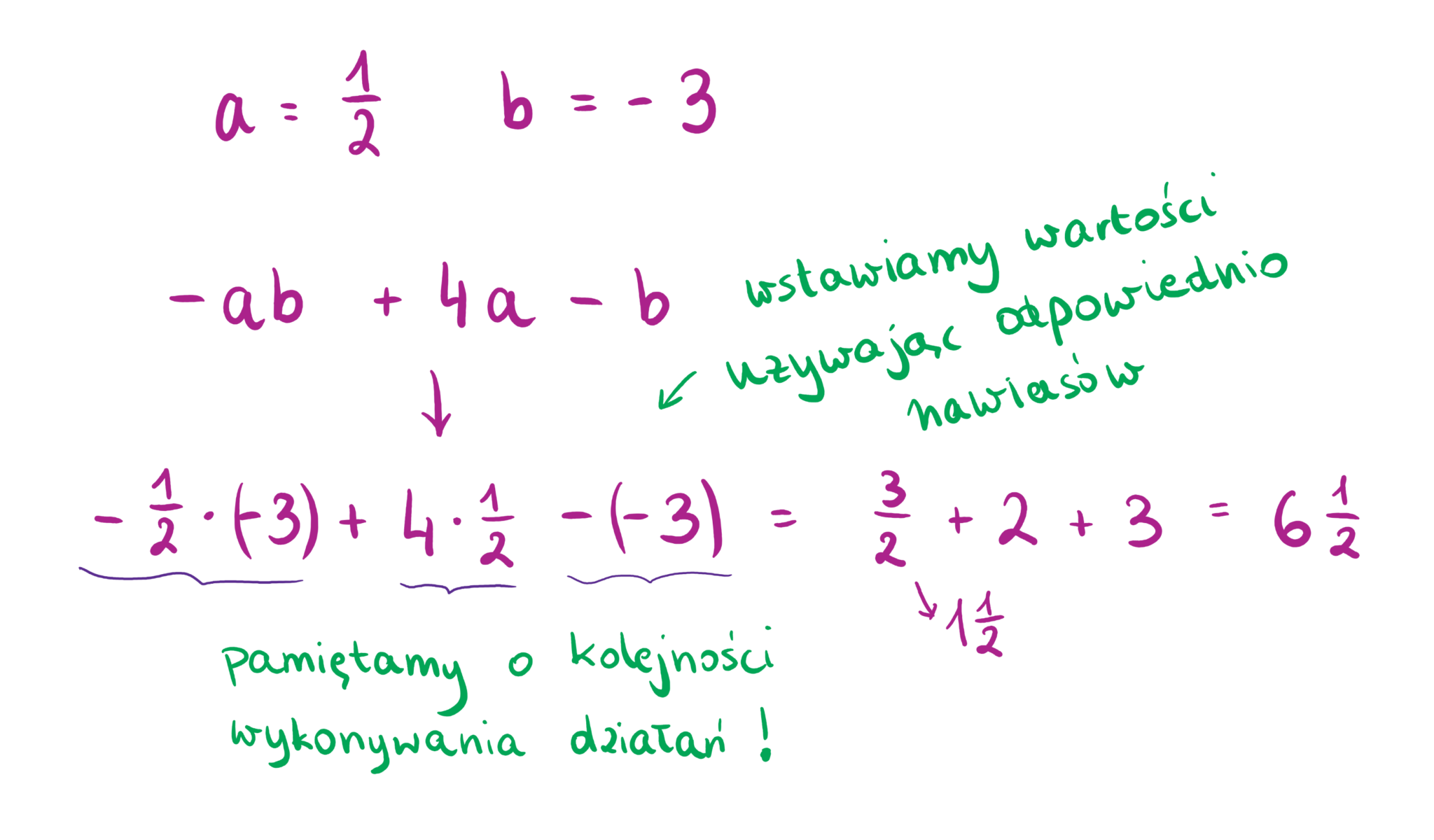


![Wyrażenia Algebraiczne I Równania Klasa 8 Sprawdzian [Klasa 8] pomoże mi ktos z matematyki "wyrażenia algebraiczne i](https://pl-static.z-dn.net/files/dad/9dfa615442689df1ac3ff59ceb417177.jpg)
