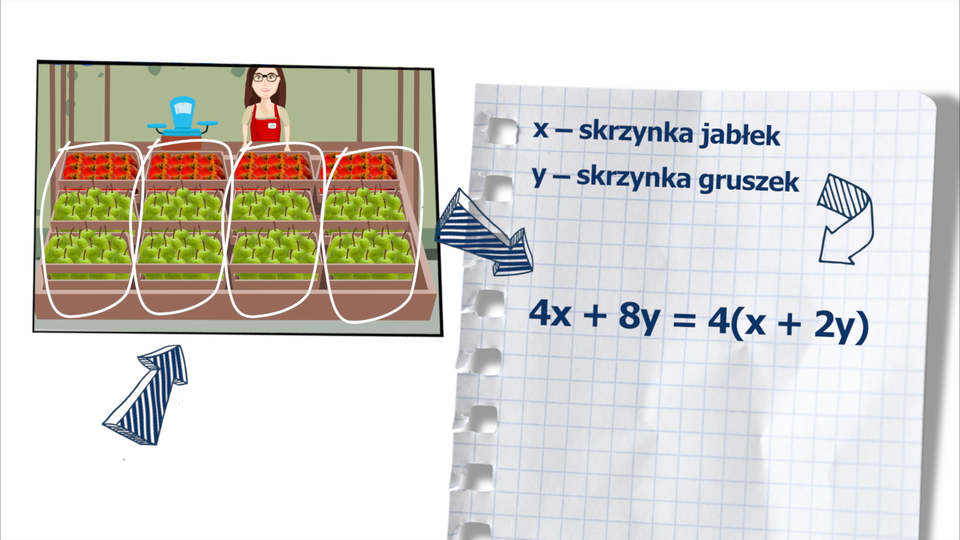
Wyłączanie Wspólnego Czynnika Przed Nawias

Czy kiedykolwiek patrzyłeś na skomplikowane wyrażenie matematyczne i czułeś się przytłoczony? Czy myślałeś, że uproszczenie go jest niemożliwe? Otóż, istnieje potężna technika, która może znacznie ułatwić Twoje życie matematyczne – wyłączanie wspólnego czynnika przed nawias. Ten artykuł jest skierowany do uczniów szkół podstawowych i średnich, studentów, a także do każdego, kto chce odświeżyć swoje umiejętności algebraiczne. Razem przejdziemy przez podstawy, zastosowania i korzyści płynące z opanowania tej kluczowej metody.

Co to jest Wyłączanie Wspólnego Czynnika Przed Nawias?

Wyłączanie wspólnego czynnika przed nawias to technika algebraiczna, która pozwala uprościć wyrażenia poprzez identyfikację i wyodrębnienie wspólnego czynnika z kilku składników. Innymi słowy, szukamy czegoś, co *dzieli się* przez każdy element w wyrażeniu i umieszczamy to "na zewnątrz" nawiasu, a wewnątrz pozostawiamy resztę. Wyobraź sobie to jak wyciąganie wspólnego składnika z mieszanki różnych składników – identyfikujesz, co mają wspólnego, i wyodrębniasz to na zewnątrz.

Podstawowe Zasady

Aby skutecznie wyłączać wspólny czynnik przed nawias, musimy pamiętać o kilku kluczowych zasadach:

• Znajdź Największy Wspólny Dzielnik (NWD): To jest kluczowy krok. Musimy zidentyfikować największy możliwy czynnik, który dzieli się przez wszystkie terminy w wyrażeniu.
• Podziel Każdy Term na NWD: Po znalezieniu NWD, dzielimy każdy term w wyrażeniu przez ten NWD.
• Zapisz NWD przed Nawiasem: Umieszczamy zidentyfikowany NWD przed nawiasem.
• Wpisz Wyniki Dzielenia do Nawiasu: Wewnątrz nawiasu zapisujemy wyniki dzielenia każdego termu przez NWD, oddzielając je znakami dodawania lub odejmowania, które były oryginalnie w wyrażeniu.

Przykładowo, rozważmy wyrażenie: 6x + 9y.

1. NWD dla 6 i 9 to 3.
2. Dzielimy każdy term przez 3: 6x / 3 = 2x oraz 9y / 3 = 3y.
3. Zapisujemy 3 przed nawiasem: 3( ).
4. Wpisujemy wyniki dzielenia do nawiasu: 3(2x + 3y).

Otrzymujemy więc: 6x + 9y = 3(2x + 3y). Uproszczone, prawda?

Kiedy i Dlaczego Używać Tej Metody?

Wyłączanie wspólnego czynnika przed nawias jest niezwykle użyteczne w różnych sytuacjach matematycznych. Oto kilka przykładów:

• Upraszczanie Wyrażeń Algebraicznych: Jak widzieliśmy wcześniej, pozwala to na redukcję skomplikowanych wyrażeń do prostszej formy, co ułatwia dalsze obliczenia.
• Rozwiązywanie Równań: Często uproszczenie równania poprzez wyłączenie wspólnego czynnika jest kluczowe do znalezienia rozwiązania.
• Faktoryzacja: Jest to podstawowa technika faktoryzacji wielomianów, co jest fundamentalne w algebrze.
• Redukcja Ułamków Algebraicznych: Upraszczanie liczników i mianowników ułamków algebraicznych często wymaga wyłączenia wspólnego czynnika.

Dlaczego to robimy? Upraszczanie wyrażeń i równań nie tylko czyni je łatwiejszymi do zrozumienia, ale także zmniejsza ryzyko popełnienia błędów podczas obliczeń. Wyobraź sobie, że musisz rozwiązać równanie z wieloma skomplikowanymi termami. Wyłączenie wspólnego czynnika może znacznie zredukować ilość kroków i obliczeń potrzebnych do znalezienia odpowiedzi.

Przykłady i Ćwiczenia

Najlepszym sposobem na opanowanie tej techniki jest praktyka. Oto kilka przykładów i ćwiczeń, które pomogą Ci zrozumieć i zastosować wyłączanie wspólnego czynnika przed nawias.

Przykład 1: Prosty przykład

Uprość wyrażenie: 4a + 8b

1. NWD dla 4 i 8 to 4.
2. 4a / 4 = a oraz 8b / 4 = 2b.
3. Wynik: 4(a + 2b)

Przykład 2: Wyrażenie z Minusem

Uprość wyrażenie: 15x - 25y

1. NWD dla 15 i 25 to 5.
2. 15x / 5 = 3x oraz -25y / 5 = -5y.
3. Wynik: 5(3x - 5y)

Przykład 3: Wyrażenie z Więcej niż Dwoma Termami

Uprość wyrażenie: 12p + 18q - 6r

1. NWD dla 12, 18 i 6 to 6.
2. 12p / 6 = 2p, 18q / 6 = 3q oraz -6r / 6 = -r.
3. Wynik: 6(2p + 3q - r)

Przykład 4: Wyrażenia z Zmiennymi w Potędze

Uprość wyrażenie: x² + 5x

1. Wspólny czynnik to x (ponieważ x² to x * x).
2. x² / x = x oraz 5x / x = 5.
3. Wynik: x(x + 5)

Ćwiczenia Dla Ciebie

Spróbuj uprościć następujące wyrażenia samodzielnie:

• 10c + 15d
• 21m - 14n
• 8x + 12y + 4z
• a³ - 2a²
• 9p²q + 6pq²

Pamiętaj, kluczem do sukcesu jest regularna praktyka. Im więcej ćwiczysz, tym łatwiej będzie Ci identyfikować wspólne czynniki i upraszczać wyrażenia.

Trudniejsze Przykłady i Pułapki

Czasami wyłączanie wspólnego czynnika przed nawias może być bardziej skomplikowane. Oto kilka przykładów z większą ilością pułapek:

Przykład 5: Wyrażenia z Dużymi Liczbami

Uprość wyrażenie: 72a + 108b

Znalezienie NWD dla 72 i 108 może wydawać się trudne. Można użyć algorytmu Euklidesa lub rozłożyć obie liczby na czynniki pierwsze. W tym przypadku NWD to 36.

1. 72a / 36 = 2a oraz 108b / 36 = 3b.
2. Wynik: 36(2a + 3b)

Przykład 6: Wyrażenia z Ułamkami

Uprość wyrażenie: (1/2)x + (1/4)y

Można wyłączyć ułamek jako wspólny czynnik. W tym przypadku NWD to 1/4.

1. (1/2)x / (1/4) = 2x oraz (1/4)y / (1/4) = y.
2. Wynik: (1/4)(2x + y)

Przykład 7: Wyrażenia z Złożonymi Zmiennymi

Uprość wyrażenie: a²b + ab²

Tutaj wspólnym czynnikiem jest *ab*.

1. a²b / ab = a oraz ab² / ab = b.
2. Wynik: ab(a + b)

Pułapki, Na Które Trzeba Uważać

• Nie Wyłączanie Największego Wspólnego Dzielnika: Zawsze szukaj największego możliwego czynnika. Wyłączenie mniejszego czynnika sprawi, że wyrażenie będzie nadal do uproszczenia.
• Błędy w Dzieleniu: Upewnij się, że dokładnie dzielisz każdy term przez wspólny czynnik. Błąd w dzieleniu spowoduje nieprawidłowe uproszczenie.
• Zapominanie o Znaku Minus: Pamiętaj o znakach plus i minus podczas wpisywania wyników dzielenia do nawiasu.

Jak To Się Ma do Życia Codziennego?

Choć wyłączanie wspólnego czynnika przed nawias może wydawać się czysto matematyczną koncepcją, tak naprawdę ma ona zastosowanie w wielu aspektach naszego życia. Wyobraź sobie, że planujesz przyjęcie i musisz kupić napoje i przekąski. Jeśli wiesz, że każda osoba zje 2 kawałki pizzy i wypije 3 napoje, możesz obliczyć całkowity koszt, wyłączając wspólny czynnik (liczbę osób). Podobnie, jeśli obliczasz budżet domowy i widzisz, że masz pewne stałe wydatki co miesiąc, możesz wyłączyć te wydatki, aby lepiej zrozumieć, ile pieniędzy Ci zostaje na inne cele.

"Matematyka jest wszędzie wokół nas. To nie tylko równania w książkach, ale sposób myślenia i rozwiązywania problemów w życiu."

Anonimowy Matematyk

Podsumowanie i Dalsze Kroki

Opanowanie wyłączania wspólnego czynnika przed nawias to fundamentalna umiejętność algebraiczna, która otwiera drzwi do bardziej zaawansowanych koncepcji matematycznych. Ułatwia upraszczanie wyrażeń, rozwiązywanie równań i faktoryzację, co czyni ją nieocenioną w edukacji i życiu codziennym.

Kluczowe Wnioski

• Definicja: Wyłączanie wspólnego czynnika przed nawias to technika upraszczania wyrażeń poprzez wyodrębnienie wspólnego czynnika.
• Zasady: Znajdź NWD, podziel każdy term, zapisz NWD przed nawiasem, wpisz wyniki dzielenia do nawiasu.
• Zastosowania: Upraszczanie wyrażeń, rozwiązywanie równań, faktoryzacja, redukcja ułamków algebraicznych.
• Praktyka: Regularne ćwiczenia są kluczem do opanowania tej techniki.

Dalsze Kroki

• Ćwicz Więcej: Znajdź więcej przykładów i ćwiczeń online lub w podręcznikach.
• Szukaj Pomocy: Jeśli masz trudności, skonsultuj się z nauczycielem, korepetytorem lub kolegą.
• Stosuj w Praktyce: Szukaj okazji do zastosowania tej techniki w rozwiązywaniu problemów matematycznych.

Pamiętaj, że matematyka to umiejętność, która rozwija się z czasem i praktyką. Nie zrażaj się trudnościami, a z czasem zobaczysz, jak Twoje umiejętności algebraiczne rosną! Powodzenia!