Wyłącz Czynnik Pod Znak Pierwiastka

Zapewne znasz to uczucie. Siedzisz nad zadaniem z matematyki, wpatrujesz się w pierwiastek, pod którym kryje się długa liczba, i czujesz narastającą frustrację. „Czy naprawdę muszę to obliczać?” – myślisz. A może nawet: „Kiedy to mi się w życiu przyda?!”. Rozumiem to. Matematyka bywa zniechęcająca, szczególnie gdy operacje wydają się oderwane od rzeczywistości. Ale spokojnie, dzisiaj spróbujemy to zmienić. Porozmawiamy o wyłączaniu czynnika przed znak pierwiastka – o czymś, co na pierwszy rzut oka wygląda na abstrakcyjny trik, ale w rzeczywistości może uprościć Twoje obliczenia i pomóc Ci lepiej zrozumieć świat liczb.

Ten artykuł ma za zadanie pokazać Ci, że wyłączanie czynnika przed znak pierwiastka nie jest tylko bezużyteczną regułką w podręczniku. Spróbujemy zrozumieć *dlaczego* to robimy i *gdzie* można to wykorzystać. Postaram się wyjaśnić to w sposób przystępny, bez nadmiernego żargonu matematycznego. Bo matematyka, wbrew pozorom, jest fascynująca. Musimy tylko znaleźć odpowiedni klucz, by ją zrozumieć.

Dlaczego w ogóle zawracać sobie tym głowę?

Zanim przejdziemy do konkretów, zastanówmy się: po co w ogóle wyłączać czynnik przed znak pierwiastka? Czy nie możemy po prostu zostawić tej liczby pod pierwiastkiem i zapomnieć o problemie?

Otóż, wyłączanie czynnika przed znak pierwiastka ma kilka istotnych zalet:

• Upraszcza wyrażenia: Wyobraź sobie, że masz obliczyć pole prostokąta, którego jeden bok ma długość √75, a drugi √3. Bez wyłączania czynnika przed znak pierwiastka musisz pomnożyć √75 * √3 = √225 = 15. Natomiast wyłączając czynnik, masz 5√3 * √3 = 5 * 3 = 15. W tym przypadku różnica nie jest kolosalna, ale w bardziej skomplikowanych przykładach uproszczenie jest znaczące.
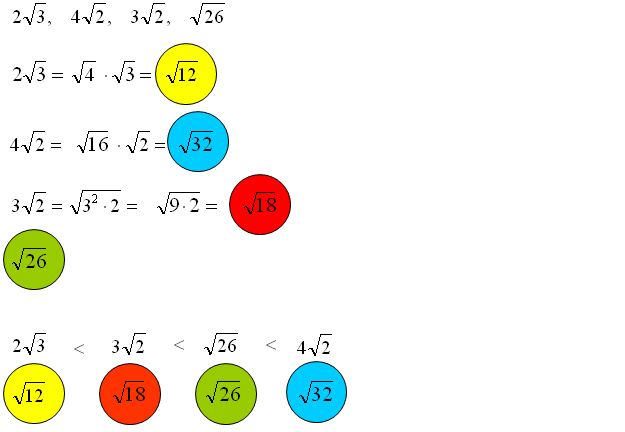
• Ułatwia porównywanie liczb: Porównanie √48 i 3√3 jest trudniejsze, niż porównanie 4√3 i 3√3. Po wyłączeniu czynnika przed znak pierwiastka natychmiast widzimy, która liczba jest większa.
• Ułatwia wykonywanie działań: Dodawanie i odejmowanie pierwiastków jest możliwe tylko wtedy, gdy mają one tę samą liczbę pod pierwiastkiem. Wyłączając czynnik przed znak pierwiastka, możemy doprowadzić do sytuacji, w której będziemy mogli te pierwiastki dodać lub odjąć.
• Przybliża nas do rzeczywistości: W praktycznych zastosowaniach, np. w fizyce czy inżynierii, często operujemy na wartościach przybliżonych. Wyłączenie czynnika przed znak pierwiastka może pomóc nam oszacować wartość pierwiastka bez użycia kalkulatora.

Jak to działa? Krok po kroku.

Przejdźmy teraz do konkretów. Jak wyłączyć czynnik przed znak pierwiastka? Cała sztuka polega na tym, by znaleźć pod pierwiastkiem kwadrat jakiejś liczby. Pamiętajmy, że √(a²) = a.

Oto kroki, które należy wykonać:

1. Rozłóż liczbę pod pierwiastkiem na czynniki pierwsze: To kluczowy krok. Szukamy takich liczb, które da się zapisać jako kwadrat innej liczby. Na przykład, zamiast 12, napiszemy 2 * 2 * 3 (czyli 2² * 3).
2. Znajdź kwadraty liczb: W rozkładzie na czynniki pierwsze szukamy par identycznych liczb. Każda taka para reprezentuje kwadrat jakiejś liczby.
3. Wyciągnij kwadrat przed pierwiastek: Za każdą parę identycznych liczb wyciągamy jedną z nich przed pierwiastek. Pozostałe liczby zostają pod pierwiastkiem.

Przykład: √20

1. Rozkład na czynniki pierwsze: 20 = 2 * 2 * 5 = 2² * 5.

2. Znajdujemy kwadrat: 2².

3. Wyciągamy 2 przed pierwiastek: √20 = √(2² * 5) = 2√5.

Przykład: √72

1. Rozkład na czynniki pierwsze: 72 = 2 * 2 * 2 * 3 * 3 = 2² * 2 * 3².

2. Znajdujemy kwadraty: 2² i 3².

3. Wyciągamy 2 i 3 przed pierwiastek: √72 = √(2² * 2 * 3²) = 2 * 3 * √2 = 6√2.

Gdzie to się przydaje? Przykłady z życia.

Może się zastanawiasz: "Ok, rozumiem jak to się robi, ale po co mi to w życiu?". Słuszne pytanie. Oto kilka przykładów, gdzie wyłączanie czynnika przed znak pierwiastka może być przydatne:

• Geometria: Obliczanie długości przekątnej kwadratu lub wysokości trójkąta równobocznego. Wzory często zawierają pierwiastki. Upraszczanie tych pierwiastków ułatwia dalsze obliczenia.
• Fizyka: Obliczanie prędkości, energii kinetycznej, czy okresu drgań wahadła. Wzory w fizyce nierzadko zawierają pierwiastki kwadratowe.
• Informatyka: W algorytmach graficznych i geometrycznych, np. przy obliczaniu odległości między punktami.
• Budownictwo: Obliczanie długości belek, przekątnych, czy powierzchni.
• Nawigacja: Określanie odległości na mapach (szczególnie przy użyciu twierdzenia Pitagorasa).

Wyobraź sobie sytuację, w której budujesz altankę w ogrodzie. Musisz obliczyć długość krokwi dachowych. Używasz twierdzenia Pitagorasa i otrzymujesz wynik w postaci √18 metrów. Czy powiesz stolarzowi: "Proszę o krokiew o długości pierwiastek z osiemnastu metrów"? Prawdopodobnie nie. Wyłączysz czynnik przed znak pierwiastka: √18 = √(3² * 2) = 3√2. A ponieważ wiesz, że √2 ≈ 1.41, możesz łatwo oszacować, że potrzebujesz krokwi o długości około 3 * 1.41 = 4.23 metra. To już jest informacja, z którą stolarz może pracować!

Argumenty przeciwne? A może jednak niepotrzebne?

Niektórzy mogą argumentować, że w dobie kalkulatorów i komputerów, wyłączanie czynnika przed znak pierwiastka jest zbędne. Przecież możemy po prostu wpisać liczbę pod pierwiastkiem w kalkulator i otrzymać wynik. To prawda, ale…

Po pierwsze, nie zawsze mamy dostęp do kalkulatora. Po drugie, kalkulator daje nam wynik przybliżony. Wyłączanie czynnika przed znak pierwiastka pozwala nam na uzyskanie wyniku dokładnego (w postaci wyrażenia z pierwiastkiem). Po trzecie, i być może najważniejsze, rozumienie, dlaczego coś robimy, jest ważniejsze niż samo bezmyślne wklepywanie liczb w kalkulator. Wyłączanie czynnika przed znak pierwiastka pomaga nam lepiej zrozumieć strukturę liczb i relacje między nimi. To rozwija nasze myślenie matematyczne.

Kolejny argument to taki, że w bardziej zaawansowanej matematyce (np. na studiach) rzadko kiedy ręcznie wyłączamy czynniki. Zgadza się. Ale zrozumienie tego procesu jest fundamentem do zrozumienia bardziej skomplikowanych zagadnień. Traktujmy to jako cegiełkę w budowaniu większej wiedzy.

Kilka wskazówek i trików.

• Zapamiętaj kwadraty małych liczb: Znajomość kwadratów liczb od 1 do 15 (lub więcej) znacznie przyspieszy proces rozkładu na czynniki pierwsze.
• Szukaj największego kwadratu: Zamiast rozkładać liczbę na czynniki pierwsze krok po kroku, spróbuj od razu znaleźć największy kwadrat, który dzieli liczbę pod pierwiastkiem. Na przykład, zamiast rozkładać 48 na 2 * 2 * 2 * 2 * 3, możesz od razu zauważyć, że 48 = 16 * 3 (gdzie 16 = 4²).
• Ćwicz, ćwicz, ćwicz: Im więcej będziesz ćwiczyć, tym szybciej i sprawniej będziesz wyłączać czynnik przed znak pierwiastka.

Podsumowanie i co dalej?

Wyłączanie czynnika przed znak pierwiastka, choć na pierwszy rzut oka może wydawać się abstrakcyjnym ćwiczeniem, jest w rzeczywistości użytecznym narzędziem, które może uprościć obliczenia, ułatwić porównywanie liczb i pomóc w rozwiązywaniu problemów z różnych dziedzin. Pamiętaj, że kluczem do sukcesu jest zrozumienie *dlaczego* to robimy, a nie tylko *jak* to robimy. Mam nadzieję, że ten artykuł pomógł Ci to zrozumieć.

Teraz Twoja kolej. Spróbuj rozwiązać kilka zadań, wyłączając czynnik przed znak pierwiastka. Zacznij od prostych przykładów, a następnie przejdź do bardziej skomplikowanych. Im więcej będziesz ćwiczyć, tym lepiej to zrozumiesz.

Zastanów się, w jaki sposób możesz wykorzystać tę wiedzę w swoim życiu. Może podczas majsterkowania, planowania remontu, albo po prostu rozwiązując zadanie domowe z matematyki. Pamiętaj, że matematyka jest wszędzie wokół nas. Wystarczy tylko otworzyć oczy i zacząć ją dostrzegać.

Jakie jest pierwsze zadanie, które rozwiążesz, wykorzystując wiedzę zdobytą dzięki temu artykułowi?