Wykresy W Ruchu Jednostajnym

Czy kiedykolwiek zastanawiałeś się, jak naukowcy i inżynierowie analizują ruch obiektów? Od projektowania samochodów po przewidywanie trajektorii lotu rakiet, zrozumienie ruchu jest absolutnie kluczowe. Jednym z podstawowych, a jednocześnie niezwykle potężnych narzędzi w tym zakresie są wykresy ruchu jednostajnego. Może brzmi to skomplikowanie, ale zapewniam, że rozłożymy to na czynniki pierwsze.

Wiem, że fizyka potrafi być stresująca. Wzory, wykresy, abstrakcyjne koncepcje – łatwo się pogubić. Ale obiecuję, że skupimy się na praktycznym zrozumieniu, a nie tylko na suchych definicjach. Pokażę Ci, jak te wykresy przekładają się na realne sytuacje i dlaczego warto poświęcić im czas.

W tym artykule zanurzymy się w świat wykresów ruchu jednostajnego. Zobaczymy, co oznaczają, jak je interpretować i jak wykorzystywać do rozwiązywania problemów. Spróbujemy to zrobić tak prosto i przystępnie, jak to możliwe, bez zbędnego żargonu. Gotowy?

Czym właściwie jest ruch jednostajny?

Zanim przejdziemy do wykresów, upewnijmy się, że rozumiemy, czym jest ruch jednostajny. Najprościej mówiąc, to ruch, w którym obiekt porusza się ze stałą prędkością po linii prostej. Żadnych przyspieszeń, żadnych zakrętów, po prostu stabilna, niezmienna prędkość.

Pomyśl o samochodzie jadącym autostradą z włączonym tempomatem – jeśli nie ma wzniesień ani spadków, które by go spowolniły lub przyspieszyły, to porusza się ruchem jednostajnym (w przybliżeniu, oczywiście!). Inny przykład to astronauta dryfujący w przestrzeni kosmicznej z wyłączonym silnikiem. Po prostu leci dalej i dalej, nie zmieniając prędkości.

Przykłady ruchu jednostajnego (w przybliżeniu):

• Samochód z włączonym tempomatem na płaskiej drodze
• Człowiek idący ze stałą prędkością
• Krążek hokejowy sunący po lodzie (pomijając tarcie)
• Astronauta dryfujący w przestrzeni kosmicznej

Ważne jest, żeby zapamiętać, że ruch jednostajny jest idealizacją. W rzeczywistości bardzo trudno znaleźć idealnie jednostajny ruch, bo zawsze działają jakieś siły (tarcie, opór powietrza, itp.). Ale to uproszczenie pozwala nam zrozumieć podstawowe zasady fizyki i budować bardziej skomplikowane modele.

Wykresy ruchu jednostajnego - Klucz do zrozumienia

Teraz przejdźmy do sedna: wykresów. Dwa najważniejsze wykresy w ruchu jednostajnym to:

• Wykres położenia od czasu (x(t))
• Wykres prędkości od czasu (v(t))

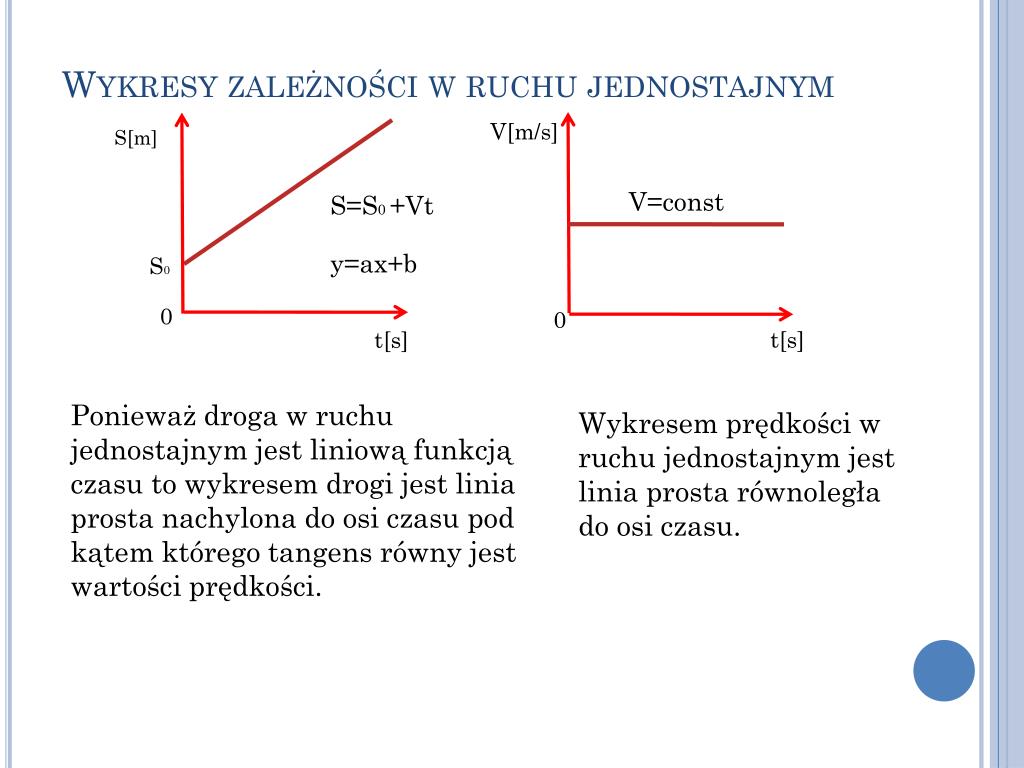
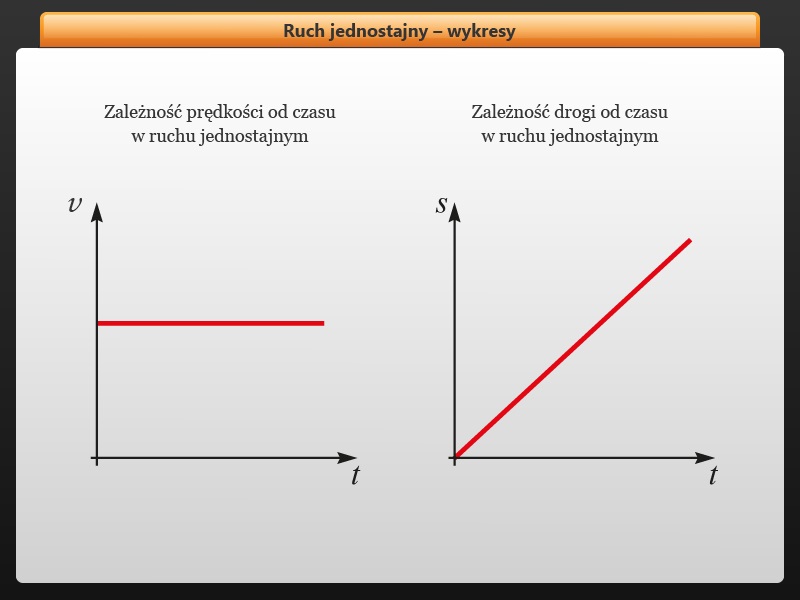
Wykres położenia od czasu (x(t))

Ten wykres pokazuje, jak zmienia się położenie obiektu w zależności od upływającego czasu. Oś pozioma reprezentuje czas (t), a oś pionowa – położenie (x).

W ruchu jednostajnym wykres położenia od czasu jest linią prostą. Dlaczego? Ponieważ obiekt pokonuje takie same odległości w takich samych odstępach czasu. Nachylenie tej prostej mówi nam o prędkości. Im bardziej stroma linia, tym większa prędkość. Linia pozioma oznacza, że obiekt się nie porusza (prędkość wynosi zero).

Analiza wykresu x(t):

• Nachylenie dodatnie: Obiekt porusza się w dodatnim kierunku (oddala się od punktu odniesienia).
• Nachylenie ujemne: Obiekt porusza się w ujemnym kierunku (zbliża się do punktu odniesienia).
• Nachylenie zero (linia pozioma): Obiekt spoczywa.
• Strome nachylenie: Duża prędkość.
• Łagodne nachylenie: Mała prędkość.

Wyobraź sobie, że masz wykres x(t) przedstawiający ruch pieszego. Jeśli linia na wykresie idzie w górę pod kątem 45 stopni, oznacza to, że pieszy porusza się ze stałą prędkością w jednym kierunku. Jeśli linia jest pozioma, pieszy stoi w miejscu.

Wykres prędkości od czasu (v(t))

Ten wykres pokazuje, jak zmienia się prędkość obiektu w zależności od upływającego czasu. Oś pozioma reprezentuje czas (t), a oś pionowa – prędkość (v).

W ruchu jednostajnym wykres prędkości od czasu jest linią poziomą. Dlaczego? Ponieważ prędkość jest stała, niezależna od czasu. Wysokość tej linii mówi nam o wartości prędkości. Jeśli linia jest powyżej osi poziomej, prędkość jest dodatnia. Jeśli linia jest poniżej osi poziomej, prędkość jest ujemna.

Analiza wykresu v(t):

• Linia pozioma powyżej osi czasu: Obiekt porusza się ze stałą prędkością w dodatnim kierunku.
• Linia pozioma poniżej osi czasu: Obiekt porusza się ze stałą prędkością w ujemnym kierunku.
• Linia pokrywająca się z osią czasu: Obiekt spoczywa.

Pole pod wykresem v(t): Jest to bardzo ważna informacja! Pole pod wykresem prędkości od czasu reprezentuje przemieszczenie obiektu. W ruchu jednostajnym, ponieważ wykres jest prostokątem, wystarczy pomnożyć prędkość przez czas, aby otrzymać przemieszczenie (czyli zmianę położenia).

Jak wykorzystać te wykresy w praktyce?

Załóżmy, że masz wykres x(t) dla pewnego obiektu i chcesz dowiedzieć się, z jaką prędkością się porusza. Po prostu znajdź dwa punkty na linii i oblicz nachylenie (zmiana położenia podzielona przez zmianę czasu).

Albo, powiedzmy, że masz wykres v(t) i chcesz obliczyć, jaką odległość pokonał obiekt w określonym czasie. Oblicz pole pod wykresem na tym przedziale czasu. To proste!

Przykładowe zadanie:

Samochód jedzie z prędkością 20 m/s przez 10 sekund. Narysuj wykres v(t) i oblicz, jaką odległość pokonał samochód.

Rozwiązanie:

Wykres v(t) to linia pozioma na wysokości 20 m/s. Pole pod tą linią to prostokąt o szerokości 10 sekund i wysokości 20 m/s. Pole prostokąta to 10 s * 20 m/s = 200 metrów. Zatem samochód pokonał 200 metrów.

Widzisz? Wykresy pozwalają nam w prosty sposób wizualizować i analizować ruch. Możemy odczytywać z nich prędkość, przemieszczenie i inne ważne informacje.

Kontrargumenty i ograniczenia

Niektórzy mogą argumentować, że ruch jednostajny to zbyt duże uproszczenie, żeby miało realne zastosowanie. I jest w tym trochę prawdy. W większości rzeczywistych sytuacji ruch jest bardziej skomplikowany – mamy do czynienia z przyspieszeniem, zmienną prędkością, zakrętami. Jednak zrozumienie ruchu jednostajnego jest fundamentalne. To podstawa, na której buduje się bardziej zaawansowane modele. Bez tego zrozumienia nie można analizować bardziej skomplikowanych zjawisk.

Inny argument to trudność w tworzeniu idealnych wykresów w realnym świecie. Pomiar prędkości i położenia zawsze wiąże się z pewnym błędem. To prawda, ale nowoczesne czujniki i oprogramowanie pozwalają na bardzo precyzyjne pomiary, co minimalizuje ten problem.

Podsumowanie i praktyczne wskazówki

Wykresy ruchu jednostajnego to potężne narzędzie do wizualizacji i analizy ruchu. Pamiętaj:

• Wykres x(t) jest linią prostą, a jego nachylenie to prędkość.
• Wykres v(t) jest linią poziomą, a pole pod nim to przemieszczenie.

Wskazówki do nauki:

• Ćwicz rysowanie i interpretowanie wykresów.
• Rozwiązuj jak najwięcej zadań.
• Spróbuj modelować realne sytuacje za pomocą wykresów.
• Używaj symulacji komputerowych do wizualizacji ruchu.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć wykresy ruchu jednostajnego. Nie zrażaj się trudnościami. Fizyka wymaga czasu i praktyki. Im więcej ćwiczysz, tym lepiej będziesz rozumieć te koncepcje.

Czy teraz, mając tę wiedzę, dostrzegasz więcej przykładów ruchu jednostajnego w swoim otoczeniu? Jakie inne zjawiska fizyczne chciałbyś zrozumieć lepiej?