Wykresy Ruchu Jednostajnie Przyspieszonego

Czy zastanawiałeś się kiedyś, jak przewidzieć ruch samochodu przyspieszającego na zielonym świetle, albo jak dokładnie działa przyspieszenie podczas jazdy na rollercoasterze? Kluczem do zrozumienia tych zjawisk są wykresy ruchu jednostajnie przyspieszonego. Ten artykuł jest skierowany do uczniów szkół średnich, studentów oraz wszystkich osób zainteresowanych fizyką, które chcą zgłębić wiedzę na temat tego fundamentalnego zagadnienia.

Czym jest ruch jednostajnie przyspieszony?

Ruch jednostajnie przyspieszony to taki rodzaj ruchu, w którym prędkość ciała zmienia się w sposób jednostajny w czasie. Oznacza to, że przyspieszenie, czyli tempo zmiany prędkości, jest stałe. Innymi słowy, jeśli ciało przyspiesza, to w każdej sekundzie jego prędkość wzrasta o taką samą wartość. Przeciwieństwem ruchu jednostajnie przyspieszonego jest ruch jednostajnie opóźniony, w którym prędkość maleje w sposób jednostajny.

Zanim przejdziemy do wykresów, warto przypomnieć sobie podstawowe pojęcia:

• Położenie (s): Określa, gdzie znajduje się ciało w danym momencie.
• Prędkość (v): Określa, jak szybko i w jakim kierunku porusza się ciało.
• Przyspieszenie (a): Określa, jak szybko zmienia się prędkość ciała.
• Czas (t): Mierzy upływ czasu.

Rodzaje Wykresów Ruchu Jednostajnie Przyspieszonego

Do analizy ruchu jednostajnie przyspieszonego używamy trzech podstawowych rodzajów wykresów:

• Wykres położenia od czasu (s-t)
• Wykres prędkości od czasu (v-t)
• Wykres przyspieszenia od czasu (a-t)

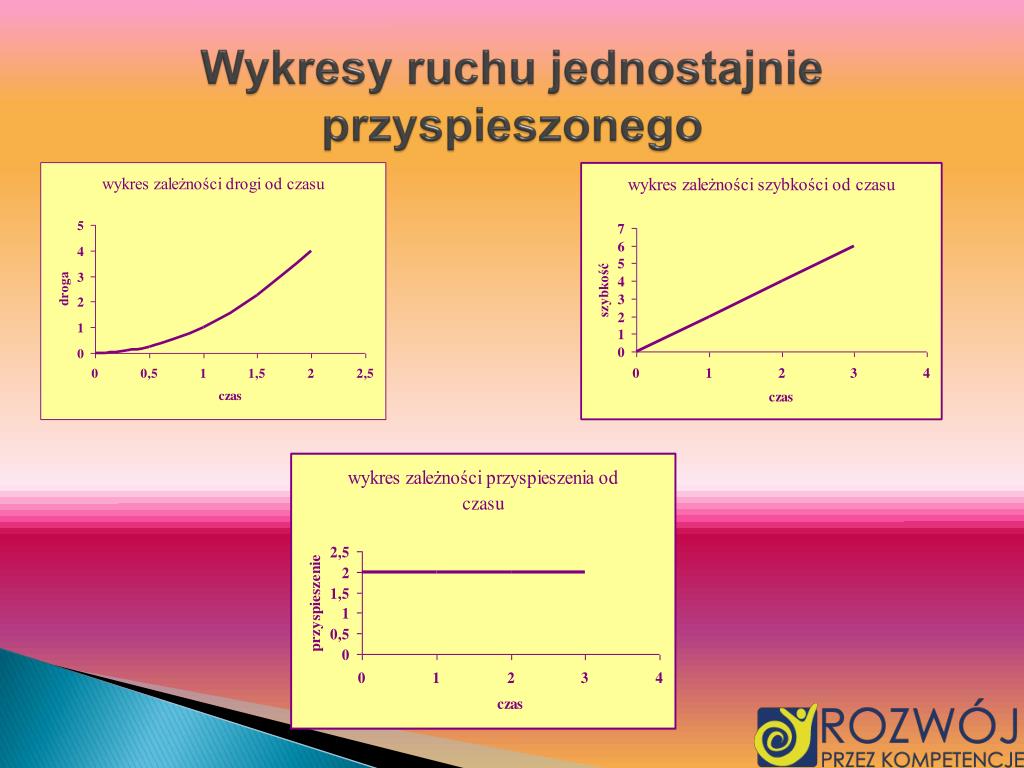
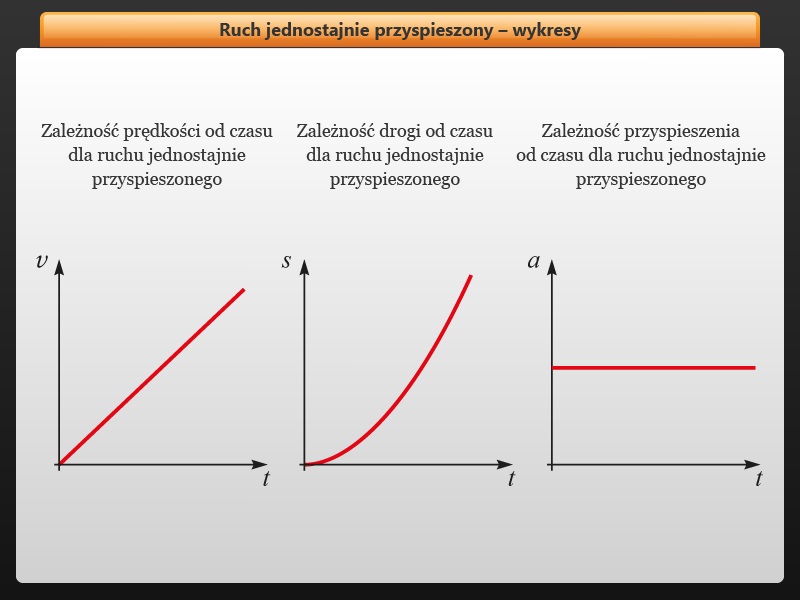
Wykres położenia od czasu (s-t)

Wykres s-t przedstawia zależność położenia ciała od czasu. W przypadku ruchu jednostajnie przyspieszonego, wykres ten ma kształt paraboli. Krzywizna paraboli zależy od wartości przyspieszenia. Im większe przyspieszenie, tym parabola jest bardziej stroma.

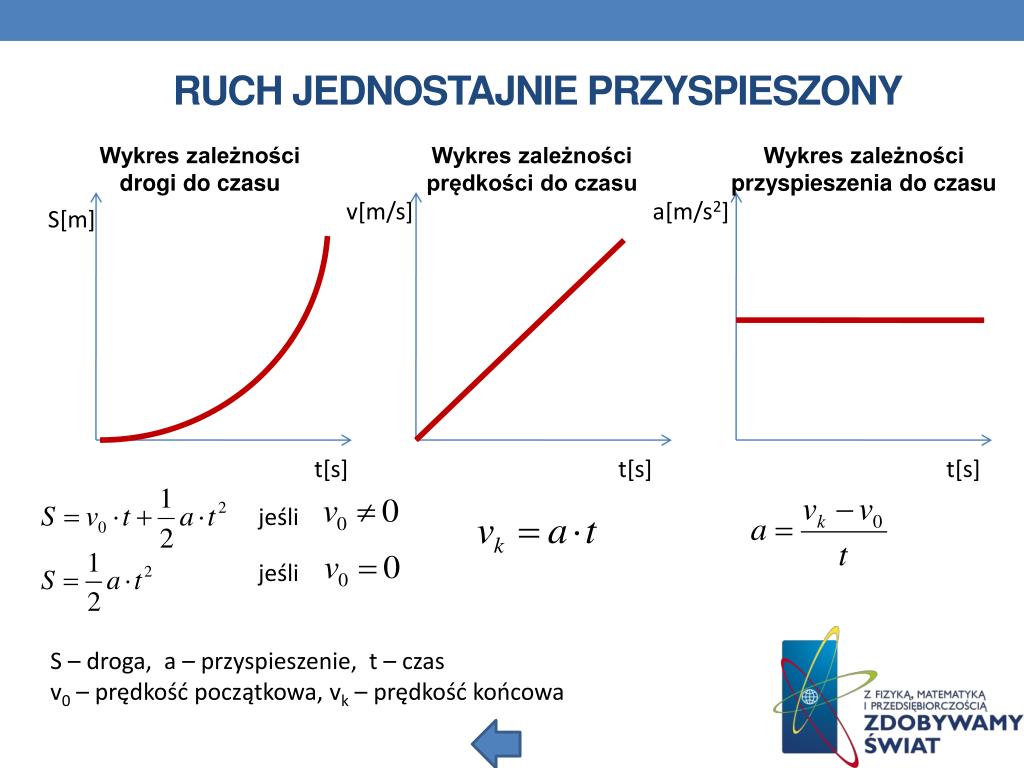
Równanie opisujące położenie w ruchu jednostajnie przyspieszonym ma postać:

s = s₀ + v₀t + (1/2)at²

Gdzie:

• s to położenie w czasie t
• s₀ to położenie początkowe
• v₀ to prędkość początkowa
• a to przyspieszenie

Zauważ, że człon (1/2)at² jest kwadratowy względem czasu, co tłumaczy paraboliczny kształt wykresu. Analizując wykres s-t, możemy odczytać położenie ciała w dowolnym momencie oraz ocenić, jak szybko zmienia się to położenie. Stromość wykresu (pochodna funkcji s(t)) w danym punkcie reprezentuje prędkość chwilową ciała w tym momencie.

Przykład: Wyobraź sobie samochód ruszający ze skrzyżowania. Początkowo samochód stoi (s₀ = 0, v₀ = 0). Po włączeniu zielonego światła, samochód zaczyna przyspieszać (a > 0). Wykres s-t będzie parabolą, która "rośnie" coraz szybciej wraz z upływem czasu.

Wykres prędkości od czasu (v-t)

Wykres v-t przedstawia zależność prędkości ciała od czasu. W ruchu jednostajnie przyspieszonym, wykres ten jest linią prostą. Nachylenie tej prostej odpowiada przyspieszeniu ciała.

Równanie opisujące prędkość w ruchu jednostajnie przyspieszonym ma postać:

v = v₀ + at

Gdzie:

• v to prędkość w czasie t
• v₀ to prędkość początkowa
• a to przyspieszenie

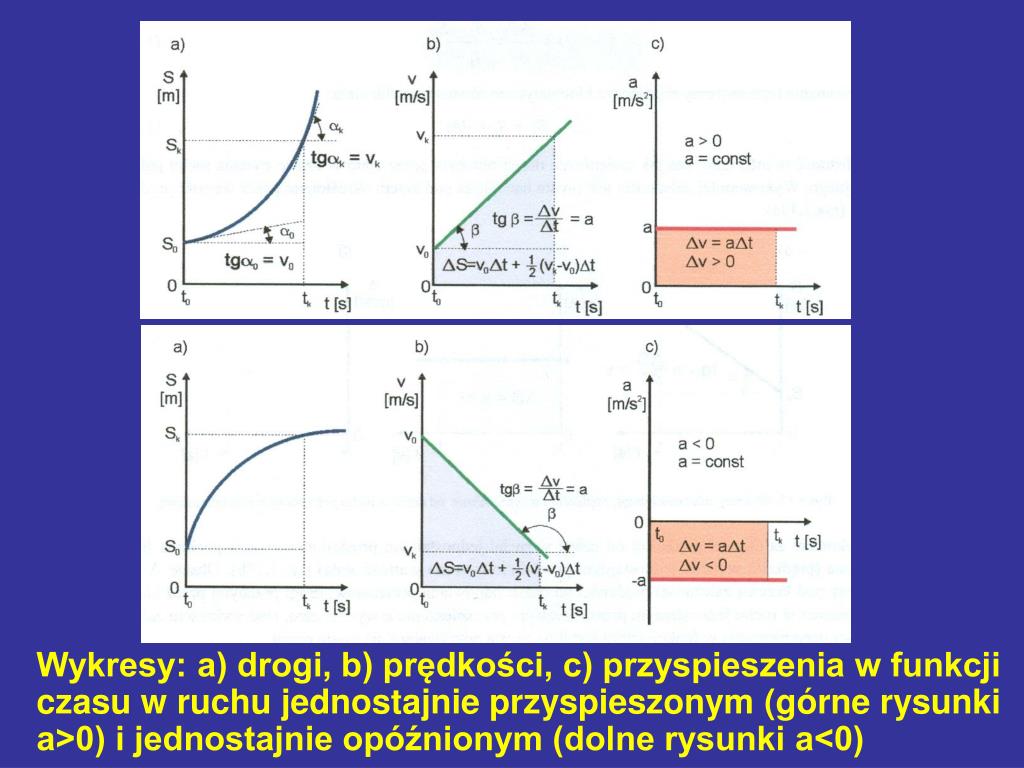
Z tego równania jasno wynika, że prędkość zmienia się liniowo w czasie. Im większe przyspieszenie (a), tym bardziej stroma jest prosta na wykresie v-t. Jeśli przyspieszenie jest dodatnie (a > 0), prędkość rośnie, a prosta wznosi się. Jeśli przyspieszenie jest ujemne (a < 0), mamy do czynienia z ruchem jednostajnie opóźnionym, a prędkość maleje, a prosta opada.

Pole pod wykresem v-t reprezentuje zmianę położenia ciała (czyli drogę) w danym przedziale czasu. Możemy obliczyć to pole jako pole trapezu lub, w prostszych przypadkach, jako pole prostokąta i trójkąta.

Przykład: Wyobraź sobie rowerzystę jadącego ze stałym przyspieszeniem. Jego prędkość początkowa wynosi 5 m/s, a przyspieszenie 1 m/s². Wykres v-t będzie linią prostą zaczynającą się od wartości 5 m/s na osi pionowej i wznoszącą się z nachyleniem odpowiadającym 1 m/s². Po 10 sekundach jazdy, rowerzysta będzie miał prędkość 15 m/s (5 + 1 * 10).

Wykres przyspieszenia od czasu (a-t)

Wykres a-t przedstawia zależność przyspieszenia ciała od czasu. W ruchu jednostajnie przyspieszonym, przyspieszenie jest stałe, więc wykres a-t jest linią poziomą.

Ponieważ przyspieszenie jest stałe, równanie opisujące ten ruch jest trywialne:

a = const.

Wartość przyspieszenia odczytujemy z osi pionowej. Jeśli linia znajduje się powyżej osi poziomej, przyspieszenie jest dodatnie. Jeśli linia znajduje się poniżej osi poziomej, przyspieszenie jest ujemne (opóźnienie).

Pole pod wykresem a-t reprezentuje zmianę prędkości ciała w danym przedziale czasu.

Przykład: Wyobraź sobie spadający swobodnie kamień (pomijamy opór powietrza). Przyspieszenie ziemskie wynosi około 9.81 m/s². Wykres a-t będzie linią poziomą na wysokości 9.81 m/s² na osi pionowej.

Zależności między wykresami

Istnieją ścisłe zależności między poszczególnymi wykresami ruchu jednostajnie przyspieszonego:

• Prędkość jest pochodną położenia po czasie (v = ds/dt). Oznacza to, że stromość wykresu s-t w danym punkcie odpowiada wartości prędkości w tym punkcie.
• Przyspieszenie jest pochodną prędkości po czasie (a = dv/dt). Oznacza to, że stromość wykresu v-t odpowiada wartości przyspieszenia.
• Zmiana położenia (droga) jest całką z prędkości po czasie. Oznacza to, że pole pod wykresem v-t reprezentuje drogę przebytą przez ciało.
• Zmiana prędkości jest całką z przyspieszenia po czasie. Oznacza to, że pole pod wykresem a-t reprezentuje zmianę prędkości ciała.

Zrozumienie tych zależności pozwala na wzajemne przekształcanie i interpretowanie wykresów, co jest kluczowe w rozwiązywaniu problemów związanych z ruchem jednostajnie przyspieszonym.

Praktyczne zastosowania

Wykresy ruchu jednostajnie przyspieszonego mają szerokie zastosowanie w różnych dziedzinach:

• Fizyka: Analiza ruchu ciał, obliczanie trajektorii, przewidywanie prędkości i położenia.
• Inżynieria: Projektowanie pojazdów, analizowanie systemów hamowania, optymalizacja ruchu robotów.
• Sport: Analiza ruchu sportowców, optymalizacja technik, projektowanie sprzętu sportowego.
• Gry komputerowe: Realistyczne symulacje ruchu obiektów.

Przykład z życia codziennego: Systemy ABS w samochodach wykorzystują zasadę ruchu jednostajnie opóźnionego. Czujniki monitorują prędkość kół i, w przypadku wykrycia blokowania, system automatycznie redukuje siłę hamowania, aby zapobiec poślizgowi. Analiza wykresów prędkości i przyspieszenia pozwala na optymalizację działania systemu ABS.

Podsumowanie

Wykresy ruchu jednostajnie przyspieszonego są potężnym narzędziem do analizy i zrozumienia ruchu, w którym prędkość zmienia się w sposób jednostajny w czasie. Zrozumienie zależności między wykresami s-t, v-t i a-t pozwala na rozwiązywanie problemów związanych z tym rodzajem ruchu oraz na przewidywanie zachowania ciał w różnych sytuacjach. Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć to zagadnienie i zachęcił do dalszego zgłębiania wiedzy z zakresu fizyki.

Pamiętaj, że kluczem do opanowania tej wiedzy jest praktyka. Rozwiązuj zadania, analizuj wykresy i staraj się dostrzegać ruch jednostajnie przyspieszony w otaczającym Cię świecie. Powodzenia!