Wykresy Ruchu Jednostajnie Prostoliniowego

Czy zastanawiałeś się kiedyś, jak naukowcy opisują ruch obiektów? Jednym z najprostszych, ale i fundamentalnych sposobów jest analiza ruchu jednostajnie prostoliniowego. Ten rodzaj ruchu, w którym ciało porusza się po linii prostej ze stałą prędkością, stanowi doskonały punkt wyjścia do zrozumienia bardziej złożonych zjawisk fizycznych. Ten artykuł jest skierowany do uczniów szkół średnich, studentów oraz wszystkich pasjonatów fizyki, którzy chcą zgłębić tajniki opisów graficznych ruchu.

Wprowadzenie do ruchu jednostajnie prostoliniowego

Ruch jednostajnie prostoliniowy charakteryzuje się dwiema kluczowymi cechami: stałą prędkością i prostoliniowym torem. Oznacza to, że ciało porusza się wzdłuż linii prostej, a jego prędkość nie ulega zmianie w czasie. To idealna sytuacja, która w realnym świecie występuje rzadko (np. w przybliżeniu ruch samochodu z włączonym tempomatem na idealnie prostej i płaskiej drodze, pomijając opory powietrza), ale jest niezwykle przydatna w nauce podstaw fizyki. Aby w pełni zrozumieć i analizować ten rodzaj ruchu, posługujemy się wykresami. Wykresy te pozwalają nam wizualizować zależność między różnymi parametrami ruchu, takimi jak położenie, prędkość i czas.

Dlaczego wykresy są tak ważne?

Wizualizacja danych za pomocą wykresów ma ogromne znaczenie w fizyce. Umożliwia szybkie i intuicyjne zrozumienie zależności między wielkościami fizycznymi. Wykresy ruchu jednostajnie prostoliniowego, a szczególnie wykresy położenia od czasu (x(t)) i prędkości od czasu (v(t)), pozwalają na:

Szybką ocenę wartości prędkości i położenia w danym momencie.
Obliczenie przebytej drogi i zmiany położenia.
Porównanie różnych ruchów.
Wykrycie nieprawidłowości w danych pomiarowych.

Rodzaje wykresów w ruchu jednostajnie prostoliniowym

W ruchu jednostajnie prostoliniowym wykorzystujemy dwa główne typy wykresów:

Wykres położenia od czasu (x(t)): Pokazuje, jak zmienia się położenie ciała w czasie.
Wykres prędkości od czasu (v(t)): Pokazuje, jak zmienia się prędkość ciała w czasie. W przypadku ruchu jednostajnie prostoliniowego, wykres ten jest szczególnie prosty.

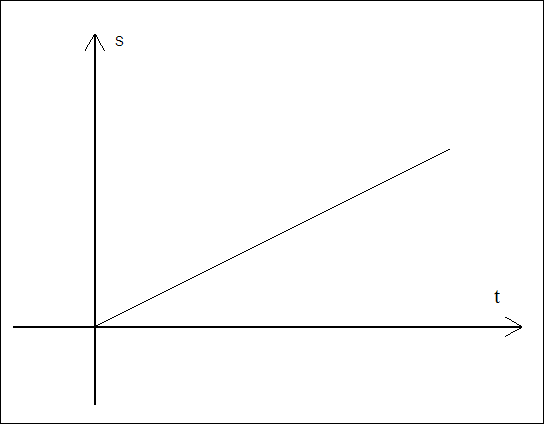
Wykres położenia od czasu (x(t))

W ruchu jednostajnie prostoliniowym wykres położenia od czasu jest linią prostą. Nachylenie tej linii odpowiada wartości prędkości. Im bardziej stroma linia, tym większa prędkość ciała. Wzór na położenie w ruchu jednostajnie prostoliniowym to:

x(t) = x₀ + v*t

Gdzie:

x(t) – położenie ciała w chwili t
x₀ – położenie początkowe ciała (w chwili t=0)
v – prędkość ciała (stała)
t – czas

Zauważ, że jest to równanie liniowe w postaci y = ax + b, gdzie y odpowiada x(t), a x odpowiada t. Współczynnik kierunkowy a to prędkość v, a wyraz wolny b to położenie początkowe x₀. Oznacza to, że interpretacja wykresu x(t) jest bezpośrednio powiązana z podstawową wiedzą z zakresu matematyki.

Interpretacja wykresu x(t):

Linia prosta rosnąca: Ciało porusza się w dodatnim kierunku (oddala się od punktu odniesienia).
Linia prosta malejąca: Ciało porusza się w ujemnym kierunku (zbliża się do punktu odniesienia).
Linia pozioma: Ciało spoczywa (prędkość równa zero).
Nachylenie linii: Im większe nachylenie (wartość bezwzględna), tym większa prędkość.
Punkt przecięcia z osią y (t=0): Pokazuje położenie początkowe x₀.

Przykład: Załóżmy, że ciało startuje z położenia x₀ = 2 metry i porusza się ze stałą prędkością v = 3 m/s. Wtedy równanie ruchu ma postać x(t) = 2 + 3t. Wykres x(t) będzie linią prostą przechodzącą przez punkt (0, 2) o nachyleniu 3.

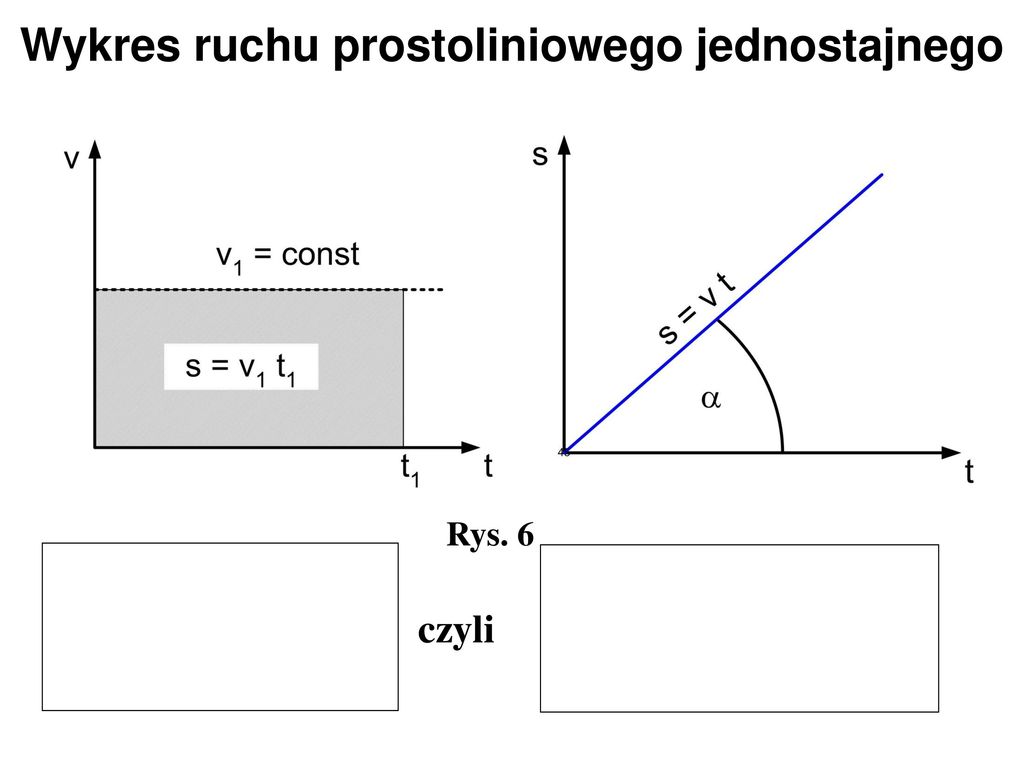
Wykres prędkości od czasu (v(t))

W ruchu jednostajnie prostoliniowym wykres prędkości od czasu jest linią poziomą. Oznacza to, że prędkość ciała jest stała i nie zmienia się w czasie. Wartość prędkości odczytujemy z osi pionowej.

Interpretacja wykresu v(t):

Linia pozioma powyżej osi x: Ciało porusza się ze stałą prędkością w dodatnim kierunku.
Linia pozioma poniżej osi x: Ciało porusza się ze stałą prędkością w ujemnym kierunku.
Linia pokrywająca się z osią x: Ciało spoczywa (prędkość równa zero).
Pole pod wykresem: Reprezentuje przemieszczenie ciała. W tym przypadku pole jest prostokątem o wysokości równej prędkości i szerokości równej czasowi. A pole prostokąta to wysokość razy szerokość, czyli v*t, co jest równe przemieszczeniu.

Obliczanie przemieszczenia z wykresu v(t):

Przemieszczenie (Δx) to zmiana położenia ciała. Możemy je obliczyć, wyznaczając pole pod wykresem prędkości od czasu:

Δx = v * Δt

Gdzie:

Δx – przemieszczenie
v – prędkość (stała)
Δt – zmiana czasu (przedział czasu)

Przykład: Jeśli ciało porusza się ze stałą prędkością v = 5 m/s przez czas Δt = 10 sekund, to jego przemieszczenie wynosi Δx = 5 m/s * 10 s = 50 metrów. Na wykresie v(t) odpowiada to polu prostokąta o wysokości 5 m/s i szerokości 10 s.

Zastosowania wykresów ruchu jednostajnie prostoliniowego

Wykresy ruchu jednostajnie prostoliniowego mają szerokie zastosowanie w różnych dziedzinach nauki i techniki. Oto kilka przykładów:

Fizyka: Analiza ruchu ciał, obliczanie prędkości i przemieszczenia, badanie zależności między wielkościami fizycznymi.
Inżynieria: Projektowanie maszyn i urządzeń, analiza ruchu pojazdów, sterowanie robotami.
Sport: Analiza wyników sportowych, optymalizacja treningu, badanie biomechaniki ruchu.
Życie codzienne: Szacowanie czasu podróży, obliczanie prędkości pojazdów, planowanie trasy.

Przykład z życia codziennego: Wyobraź sobie, że jedziesz samochodem po autostradzie z włączonym tempomatem, utrzymując stałą prędkość 120 km/h. Wykres v(t) twojego samochodu byłby linią poziomą na poziomie 120 km/h. Jeśli jedziesz przez 2 godziny, to przebyta droga (przemieszczenie) wynosi 120 km/h * 2 h = 240 km. To pole pod wykresem v(t).

Przykładowe zadania z rozwiązaniami

Aby utrwalić zdobytą wiedzę, przeanalizujmy kilka przykładowych zadań:

Zadanie 1: Ciało porusza się ruchem jednostajnie prostoliniowym. W chwili t = 0 s jego położenie wynosi x₀ = -3 m. W chwili t = 5 s jego położenie wynosi x = 7 m. Narysuj wykres x(t) i v(t) oraz oblicz prędkość ciała.

Rozwiązanie:

1. Obliczenie prędkości:

v = (x - x₀) / t = (7 m - (-3 m)) / 5 s = 10 m / 5 s = 2 m/s

2. Wykres x(t): Jest to linia prosta przechodząca przez punkty (0, -3) i (5, 7).

3. Wykres v(t): Jest to linia pozioma na poziomie 2 m/s.

Zadanie 2: Na wykresie v(t) przedstawiono ruch jednostajnie prostoliniowy ciała. Prędkość ciała wynosi 4 m/s. Oblicz przemieszczenie ciała w przedziale czasu od 2 s do 6 s.

Rozwiązanie:

1. Obliczenie zmiany czasu: Δt = 6 s - 2 s = 4 s

2. Obliczenie przemieszczenia: Δx = v * Δt = 4 m/s * 4 s = 16 m

Zadanie 3: Samochód porusza się ruchem jednostajnym prostoliniowym z prędkością 25 m/s. Ile czasu zajmie mu pokonanie dystansu 100 metrów?

Rozwiązanie:

1. Używamy wzoru: v = Δx / t (przekształcamy go, aby wyznaczyć t)

2. Przekształcenie wzoru: t = Δx / v

3. Obliczenie czasu: t = 100 m / 25 m/s = 4 s

Podsumowanie

Wykresy ruchu jednostajnie prostoliniowego są potężnym narzędziem, które pozwala nam wizualizować i analizować ruch ciał. Rozumienie zależności między położeniem, prędkością i czasem jest kluczowe dla zrozumienia podstaw fizyki. Pamiętaj, że:

Wykres x(t) jest linią prostą, której nachylenie odpowiada prędkości.
Wykres v(t) jest linią poziomą, a pole pod nim reprezentuje przemieszczenie.

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć wykresy ruchu jednostajnie prostoliniowego. Zachęcamy do dalszego zgłębiania wiedzy z zakresu fizyki i wykorzystywania jej w praktyce!

Pamiętaj, fizyka jest wszędzie wokół nas – wystarczy uważnie obserwować i zadawać pytania!