Wykres Jednej Z Funkcji Trygonometrycznych

Zmagasz się z funkcjami trygonometrycznymi? Czujesz, że wykresy sinusa, cosinusa czy tangensa to dla Ciebie czarna magia? Nie martw się, nie jesteś sam! Wielu uczniów i studentów ma trudności z ich zrozumieniem. Często traktowane są jako abstrakcyjne pojęcia matematyczne, bez związku z rzeczywistym światem. A tak naprawdę, kryją w sobie piękno i potężną moc, która znajduje zastosowanie w wielu dziedzinach życia.

Niniejszy artykuł ma na celu rozjaśnienie tematu wykresów funkcji trygonometrycznych, skupiając się na jednym z nich, aby krok po kroku pokazać, jak powstaje, jakie ma właściwości i jak możemy go wykorzystać. Zamiast suchej teorii, postaramy się łączyć matematykę z konkretnymi przykładami, które pomogą Ci zobaczyć, że funkcja trygonometryczna to nie tylko wzór, ale przede wszystkim narzędzie.

Chcemy, żebyś po przeczytaniu tego artykułu nie tylko potrafił narysować wykres wybranej funkcji trygonometrycznej, ale przede wszystkim rozumiał, co ten wykres reprezentuje i jak interpretować jego poszczególne elementy.

Wybieramy bohatera: Wykres Funkcji Sinus

Na potrzeby tego artykułu, skupimy się na funkcji sinus. Dlaczego sinus? Po pierwsze, jest to funkcja bazowa, na której opierają się inne funkcje trygonometryczne. Po drugie, jej wykres jest stosunkowo prosty i intuicyjny, co ułatwia zrozumienie podstawowych koncepcji. Po trzecie, sinus ma szerokie zastosowanie w praktyce, od analizy fal dźwiękowych po modelowanie ruchów wahadła.

Funkcja sinus, oznaczana jako f(x) = sin(x), przypisuje każdej wartości kąta (x) wartość sinusa tego kąta. Kąt x najczęściej wyrażany jest w radianach.

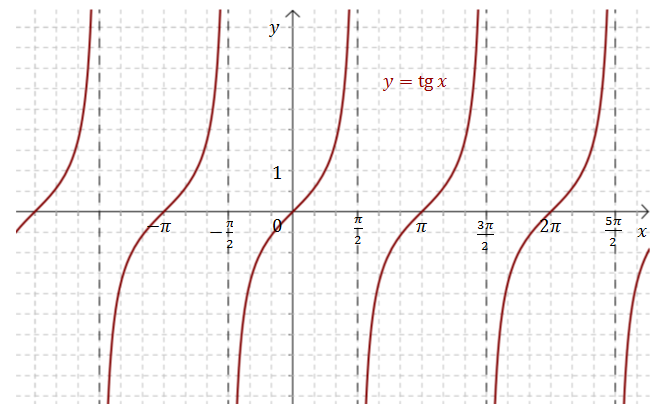
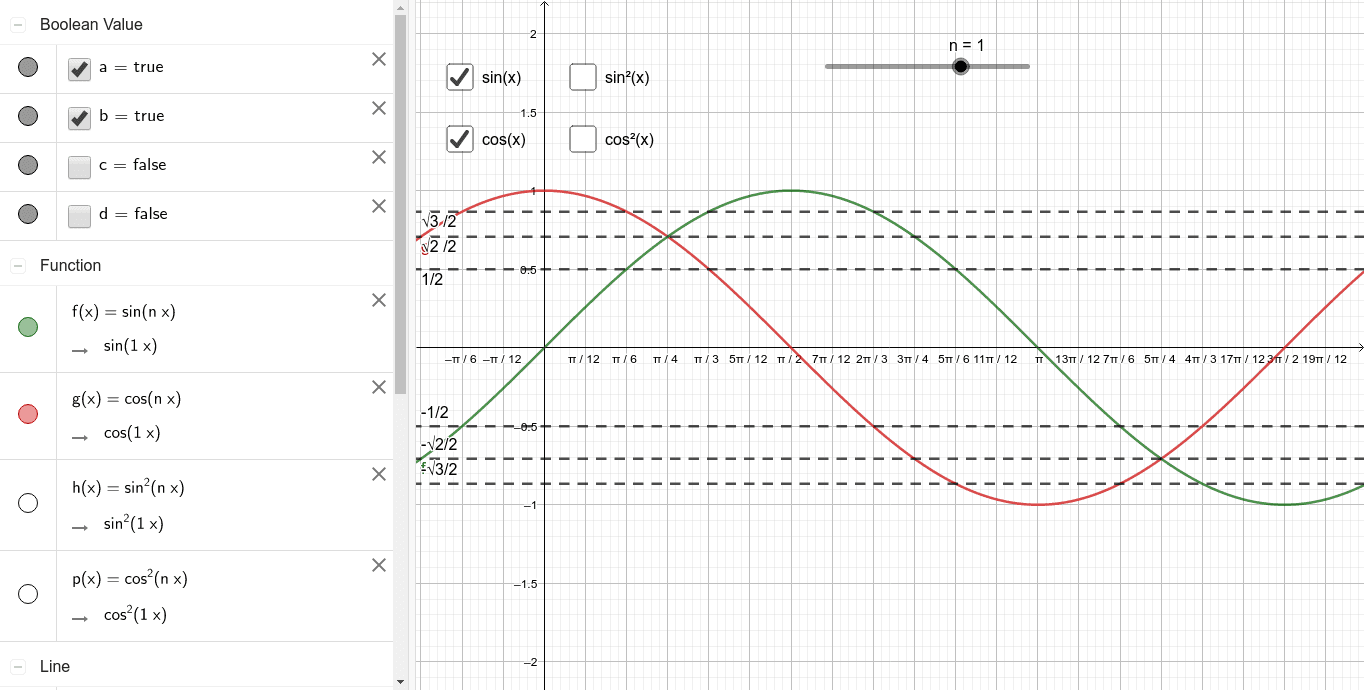
Pamiętajmy jednak, że niektórzy uważają, że skupienie się tylko na jednej funkcji jest ograniczające i lepiej byłoby przedstawić wszystkie naraz. Owszem, to prawda, ale naszym celem jest głębokie zrozumienie, a nie powierzchowne omówienie. Dlatego, opanowanie sinusa będzie solidną podstawą do dalszej nauki o cosinusie, tangensie i cotangensie.

Zanim zaczniemy rysować: Jednostka miary radian

Zanim przejdziemy do rysowania wykresu, przypomnijmy sobie, co to jest radian. Radian to jednostka miary kąta, zdefiniowana jako kąt, który wycina na okręgu łuk o długości równej promieniowi tego okręgu. Pełny kąt (360 stopni) odpowiada 2π radianów, a kąt prosty (90 stopni) odpowiada π/2 radianów. Używanie radianów upraszcza wiele wzorów i obliczeń w matematyce i fizyce, szczególnie tych związanych z funkcjami trygonometrycznymi.

• Pełny obrót: 360 stopni = 2π radianów
• Pół obrotu: 180 stopni = π radianów
• Ćwierć obrotu: 90 stopni = π/2 radianów

Wyobraź sobie koło o promieniu 1. Jeden radian to kąt, który powstaje, gdy odłożysz na obwodzie tego koła odcinek o długości równej 1. Dlatego właśnie pełny okrąg, czyli obwód o długości 2πr = 2π * 1 = 2π, odpowiada 2π radianów.

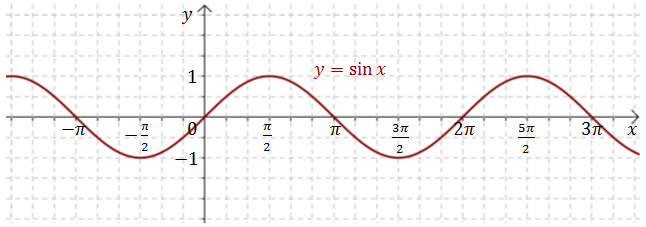
Krok po kroku: Rysujemy Wykres Funkcji Sinus

Teraz możemy przejść do sedna – rysowania wykresu funkcji sinus. Do tego potrzebujemy układu współrzędnych. Na osi poziomej (osi x) będziemy odkładali wartości kąta w radianach, a na osi pionowej (osi y) – wartości sinusa tego kąta.

1. Wybierz kilka kluczowych punktów:

   Zacznij od kilku charakterystycznych kątów, których sinus znasz na pamięć:

   • 0 radianów: sin(0) = 0
   • π/2 radianów: sin(π/2) = 1
   • π radianów: sin(π) = 0
   • 3π/2 radianów: sin(3π/2) = -1
   • 2π radianów: sin(2π) = 0

   Zaznacz te punkty w układzie współrzędnych.

2. Narysuj gładką krzywą:

   Połącz zaznaczone punkty gładką, falującą linią. Pamiętaj, że funkcja sinus jest ciągła, więc nie powinno być żadnych przerw ani ostrych załamań na wykresie. Krzywa powinna płynnie przechodzić przez zaznaczone punkty, osiągając maksimum (1) dla π/2 i minimum (-1) dla 3π/2.

3. Rozszerz wykres:

   Funkcja sinus jest okresowa, co oznacza, że jej wykres powtarza się co 2π. Dlatego, możesz po prostu skopiować narysowany fragment wykresu i przesunąć go o 2π w lewo i w prawo, aby otrzymać wykres dla szerszego zakresu wartości x.

Używając programu graficznego lub kalkulatora graficznego, możesz uzyskać dokładny i precyzyjny wykres funkcji sinus. Ale nawet ręcznie narysowany wykres, o ile wykonany starannie, pozwoli Ci zrozumieć najważniejsze cechy tej funkcji.

Charakterystyka Wykresu Funkcji Sinus

Po narysowaniu wykresu, przyjrzyjmy się jego najważniejszym cechom:

• Okresowość: Funkcja sinus jest okresowa, co oznacza, że jej wartości powtarzają się regularnie. Okres funkcji sinus wynosi 2π. Oznacza to, że sin(x + 2π) = sin(x) dla każdego x.
• Amplituda: Amplituda funkcji sinus to odległość między osią x a maksymalną (lub minimalną) wartością funkcji. W przypadku standardowej funkcji sinus, amplituda wynosi 1.
• Dziedzina: Dziedziną funkcji sinus jest zbiór wszystkich liczb rzeczywistych (x ∈ R). Oznacza to, że możemy obliczyć sinus dowolnego kąta.
• Zbiór wartości: Zbiorem wartości funkcji sinus jest przedział [-1, 1]. Oznacza to, że wartości sinusa zawsze mieszczą się w przedziale od -1 do 1 włącznie.
• Miejsca zerowe: Miejsca zerowe funkcji sinus to wartości x, dla których sin(x) = 0. Miejsca zerowe funkcji sinus to: 0, π, 2π, -π, -2π i tak dalej, czyli kπ, gdzie k jest liczbą całkowitą.
• Symetria: Funkcja sinus jest nieparzysta, co oznacza, że sin(-x) = -sin(x). Graficznie, oznacza to, że wykres funkcji sinus jest symetryczny względem początku układu współrzędnych.

Ważne: Zrozumienie tych cech jest kluczowe do interpretacji wykresów funkcji sinus i wykorzystywania ich w praktycznych zastosowaniach.

Transformacje Wykresu Funkcji Sinus

Wykres funkcji sinus można przekształcać na różne sposoby, co pozwala modelować bardziej złożone zjawiska. Najczęściej spotykane transformacje to:

• Zmiana amplitudy: Funkcja f(x) = A * sin(x) ma amplitudę równą |A|. Jeśli A jest większe od 1, wykres jest "rozciągnięty" w pionie. Jeśli A jest mniejsze od 1 (ale większe od 0), wykres jest "ściśnięty" w pionie.
• Zmiana okresu: Funkcja f(x) = sin(B * x) ma okres równy 2π/|B|. Jeśli B jest większe od 1, okres jest krótszy (wykres jest "ściśnięty" w poziomie). Jeśli B jest mniejsze od 1, okres jest dłuższy (wykres jest "rozciągnięty" w poziomie).
• Przesunięcie w pionie: Funkcja f(x) = sin(x) + C jest przesunięta w pionie o C jednostek. Jeśli C jest dodatnie, wykres jest przesunięty w górę. Jeśli C jest ujemne, wykres jest przesunięty w dół.
• Przesunięcie w poziomie (przesunięcie fazowe): Funkcja f(x) = sin(x - D) jest przesunięta w poziomie o D jednostek. Jeśli D jest dodatnie, wykres jest przesunięty w prawo. Jeśli D jest ujemne, wykres jest przesunięty w lewo.

Wyobraź sobie falę na morzu. Zmiana amplitudy to zmiana wysokości fali. Zmiana okresu to zmiana odległości między falami. Przesunięcie w pionie to przesunięcie całej powierzchni wody w górę lub w dół. A przesunięcie w poziomie to przesunięcie całej fali w lewo lub w prawo.

Praktyczne Zastosowania Funkcji Sinus

Funkcja sinus ma liczne zastosowania w różnych dziedzinach:

• Fizyka: Opis fal, drgań, ruchu harmonicznego prostego (np. ruch wahadła), prądu przemiennego, fal dźwiękowych i świetlnych. Analiza sygnałów.
• Informatyka: Generowanie dźwięków, tworzenie animacji, kompresja danych.
• Inżynieria: Projektowanie układów elektronicznych, analiza drgań konstrukcji, modelowanie fal morskich.
• Matematyka: Rozwiązywanie równań trygonometrycznych, geometria, analiza zespolona.
• Muzyka: Analiza i synteza dźwięku.
• Medycyna: Analiza rytmu serca (EKG).

Na przykład, prąd przemienny w gniazdku elektrycznym ma przebieg sinusoidalny. Jego napięcie zmienia się w czasie zgodnie z funkcją sinus. Dzięki temu możemy zasilać urządzenia elektryczne i przesyłać energię na duże odległości. Kolejnym przykładem jest dźwięk. Każdy dźwięk można rozłożyć na sumę fal sinusoidalnych o różnych częstotliwościach i amplitudach. To pozwala nam analizować i syntetyzować dźwięki, a także tworzyć muzykę.

Istnieją argumenty, że symulacje komputerowe są bardziej efektywnym sposobem na zrozumienie zjawisk fizycznych. Chociaż to prawda, że symulacje mogą zapewnić wizualizacje i interaktywne doświadczenia, zrozumienie matematycznych fundamentów, takich jak funkcja sinus, jest niezbędne do interpretacji wyników symulacji i krytycznego myślenia o modelowanych zjawiskach. Symulacje są narzędziem, ale wiedza o podstawach matematyki jest fundamentem.

Podsumowanie

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć wykres funkcji sinus. Pamiętaj, że kluczem do sukcesu jest praktyka. Spróbuj samodzielnie narysować wykres funkcji sinus, eksperymentować z różnymi transformacjami i szukać zastosowań funkcji sinus w otaczającym Cię świecie. Im więcej będziesz ćwiczyć, tym lepiej zrozumiesz tę ważną funkcję trygonometryczną.

Teraz, gdy masz już solidne podstawy, zachęcamy Cię do dalszej eksploracji innych funkcji trygonometrycznych: cosinusa, tangensa i cotangensa. Porównaj ich wykresy, znajdź różnice i podobieństwa, i przekonaj się, jak wszechstronne i potężne są te narzędzia matematyczne.

Czy teraz, patrząc na falę na morzu lub słuchając ulubionej piosenki, dostrzegasz obecność funkcji sinus? Czy zastanawiasz się, jak jej wykres opisuje te zjawiska?