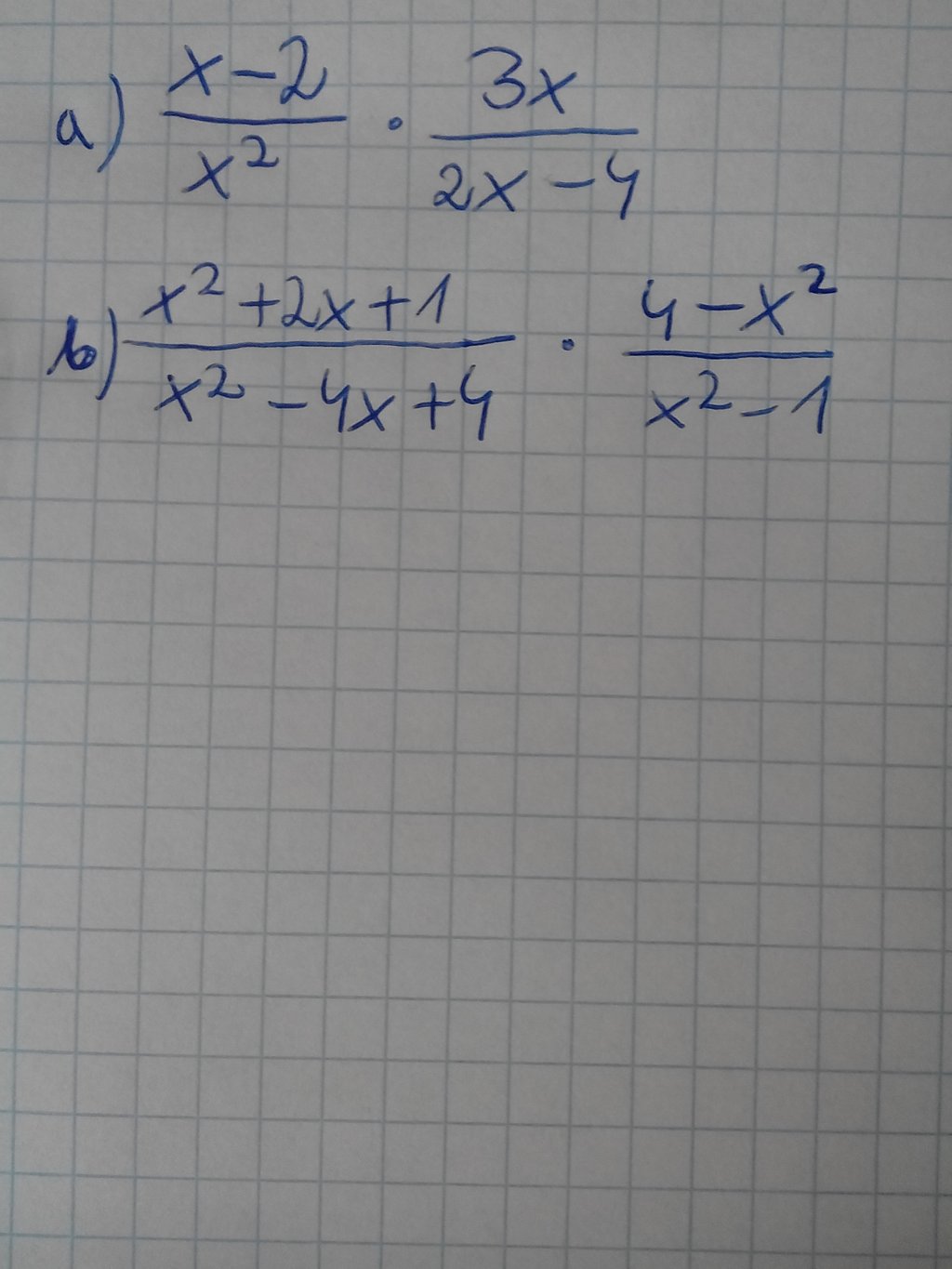Wykonaj Mnożenie Odpowiedź Podaj W Najprostszej Postaci

Opanuj sztukę mnożenia ułamków! To prostsze niż myślisz, a wynik zawsze możesz uprościć do najmniejszej możliwej postaci. Pokażemy, jak to zrobić krok po kroku, żebyś mógł bez problemu rozwiązywać zadania z ułamkami. Przygotuj się na serię przykładów i wyjaśnień!

Zacznijmy od absolutnych podstaw. Jeśli masz pomnożyć dwa ułamki, powiedzmy 2/3 i 1/4, to po prostu mnożysz liczniki (górne liczby) ze sobą, a następnie mianowniki (dolne liczby) ze sobą. W tym przypadku:

(2/3) * (1/4) = (2 * 1) / (3 * 4) = 2/12

Proste, prawda? Ale to jeszcze nie koniec. Otrzymany ułamek 2/12 możemy uprościć. Zaraz do tego przejdziemy.

Kolejny przykład: 5/7 * 3/8. Postępujemy tak samo:

(5/7) * (3/8) = (5 * 3) / (7 * 8) = 15/56

W tym przypadku 15/56 jest już w najprostszej postaci, ponieważ 15 i 56 nie mają wspólnych dzielników poza 1.

A co jeśli mamy liczby mieszane? Najpierw trzeba je zamienić na ułamki niewłaściwe. Liczba mieszana składa się z części całkowitej i ułamka, na przykład 1 1/2. Żeby zamienić ją na ułamek niewłaściwy, mnożymy część całkowitą przez mianownik ułamka, dodajemy licznik i zapisujemy to wszystko nad mianownikiem:

1 1/2 = ((1 * 2) + 1) / 2 = 3/2

Teraz możemy mnożyć! Załóżmy, że mamy pomnożyć 1 1/2 przez 2/5. Najpierw zamieniamy 1 1/2 na 3/2, a następnie mnożymy:

(3/2) * (2/5) = (3 * 2) / (2 * 5) = 6/10

I znowu, trzeba uprościć!

Upraszczanie Ułamków – Klucz do Perfekcji

Upraszczanie ułamków to dzielenie licznika i mianownika przez ich największy wspólny dzielnik (NWD). NWD to największa liczba, przez którą dzielą się bez reszty zarówno licznik, jak i mianownik. Wracając do przykładu 6/10:

Jak znaleźć NWD dla 6 i 10? Możemy wypisać dzielniki każdej z tych liczb:

Dzielniki 6: 1, 2, 3, 6 Dzielniki 10: 1, 2, 5, 10

Największym wspólnym dzielnikiem jest 2. Zatem dzielimy zarówno licznik, jak i mianownik przez 2:

6/10 = (6 / 2) / (10 / 2) = 3/5

I oto mamy ułamek w najprostszej postaci!

Spróbujmy z ułamkiem 2/12, który otrzymaliśmy na samym początku.

Dzielniki 2: 1, 2 Dzielniki 12: 1, 2, 3, 4, 6, 12

NWD to 2. Dzielimy:

2/12 = (2 / 2) / (12 / 2) = 1/6

Czyli (2/3) * (1/4) = 1/6

Rozważmy teraz sytuację, gdy mamy do czynienia z większymi liczbami. Na przykład 24/36. Wypisywanie wszystkich dzielników może być czasochłonne. Istnieją szybsze metody, ale na początek spróbujmy podzielić przez mniejszą liczbę, która ewidentnie dzieli zarówno 24, jak i 36. Na przykład przez 2:

24/36 = (24 / 2) / (36 / 2) = 12/18

Możemy uprościć dalej, znowu dzieląc przez 2:

12/18 = (12 / 2) / (18 / 2) = 6/9

I jeszcze raz! Tym razem podzielimy przez 3:

6/9 = (6 / 3) / (9 / 3) = 2/3

Teraz już nie da się bardziej uprościć. Czyli 24/36 w najprostszej postaci to 2/3.

A co jeśli mamy mnożenie więcej niż dwóch ułamków? Zasada jest ta sama! Mnożymy wszystkie liczniki ze sobą, a następnie wszystkie mianowniki ze sobą. Na przykład:

(1/2) * (2/3) * (3/4) = (1 * 2 * 3) / (2 * 3 * 4) = 6/24

Teraz upraszczamy. Dzielniki 6 to 1, 2, 3, 6. Dzielniki 24 to 1, 2, 3, 4, 6, 8, 12, 24. NWD to 6.

6/24 = (6 / 6) / (24 / 6) = 1/4

A co jeśli w mnożeniu występuje liczba całkowita? Liczbę całkowitą możemy zapisać jako ułamek z mianownikiem 1. Na przykład, jeśli mamy pomnożyć 3 przez 1/2, to zapisujemy 3 jako 3/1:

(3/1) * (1/2) = (3 * 1) / (1 * 2) = 3/2

I to już jest ułamek w najprostszej postaci (chociaż możemy go zapisać jako liczbę mieszaną: 1 1/2).

Przykłady Praktyczne

Sprawdźmy teraz kilka bardziej skomplikowanych przykładów, żeby utrwalić wiedzę.

Przykład 1: (2 1/4) * (1/3)

Najpierw zamieniamy 2 1/4 na ułamek niewłaściwy:

2 1/4 = ((2 * 4) + 1) / 4 = 9/4

Teraz mnożymy:

(9/4) * (1/3) = (9 * 1) / (4 * 3) = 9/12

Upraszczamy: NWD dla 9 i 12 to 3.

9/12 = (9 / 3) / (12 / 3) = 3/4

Przykład 2: (3/5) * (5/6) * (2)

Zapisujemy 2 jako 2/1:

(3/5) * (5/6) * (2/1) = (3 * 5 * 2) / (5 * 6 * 1) = 30/30 = 1

Przykład 3: (1 1/3) * (2 2/5)

Zamieniamy liczby mieszane na ułamki niewłaściwe:

1 1/3 = ((1 * 3) + 1) / 3 = 4/3 2 2/5 = ((2 * 5) + 2) / 5 = 12/5

Mnożymy:

(4/3) * (12/5) = (4 * 12) / (3 * 5) = 48/15

Upraszczamy: NWD dla 48 i 15 to 3.

48/15 = (48 / 3) / (15 / 3) = 16/5

Możemy też zapisać to jako liczbę mieszaną: 3 1/5.

Podsumowanie

Mnożenie ułamków i upraszczanie wyników to umiejętność, którą warto opanować. Pamiętaj o kilku kluczowych zasadach:

• Mnożymy liczniki ze sobą i mianowniki ze sobą.
• Liczby mieszane zamieniamy na ułamki niewłaściwe przed mnożeniem.
• Upraszczamy ułamek, dzieląc licznik i mianownik przez ich największy wspólny dzielnik (NWD).

Ćwicz regularnie, a mnożenie ułamków stanie się dla Ciebie dziecinnie proste! Im więcej przykładów rozwiążesz, tym szybciej i sprawniej będziesz radzić sobie z tego typu zadaniami. Powodzenia!