Wszystkie Wzory Na Pola Figur

Czy kiedykolwiek zastanawiałeś się, jak obliczyć, ile farby potrzebujesz do pomalowania ściany w kształcie trójkąta, albo ile materiału zużyjesz na uszycie obrusu w kształcie koła? Odpowiedź tkwi w wzorach na pola figur geometrycznych. Ten artykuł jest Twoim kompletnym przewodnikiem po tych wzorach, stworzonym z myślą o uczniach, studentach, majsterkowiczach, a także o każdym, kto chce odświeżyć swoją wiedzę z geometrii.

Podstawowe figury i ich pola

Zacznijmy od fundamentów. Poniżej znajdziesz wzory na pola najczęściej spotykanych figur płaskich:

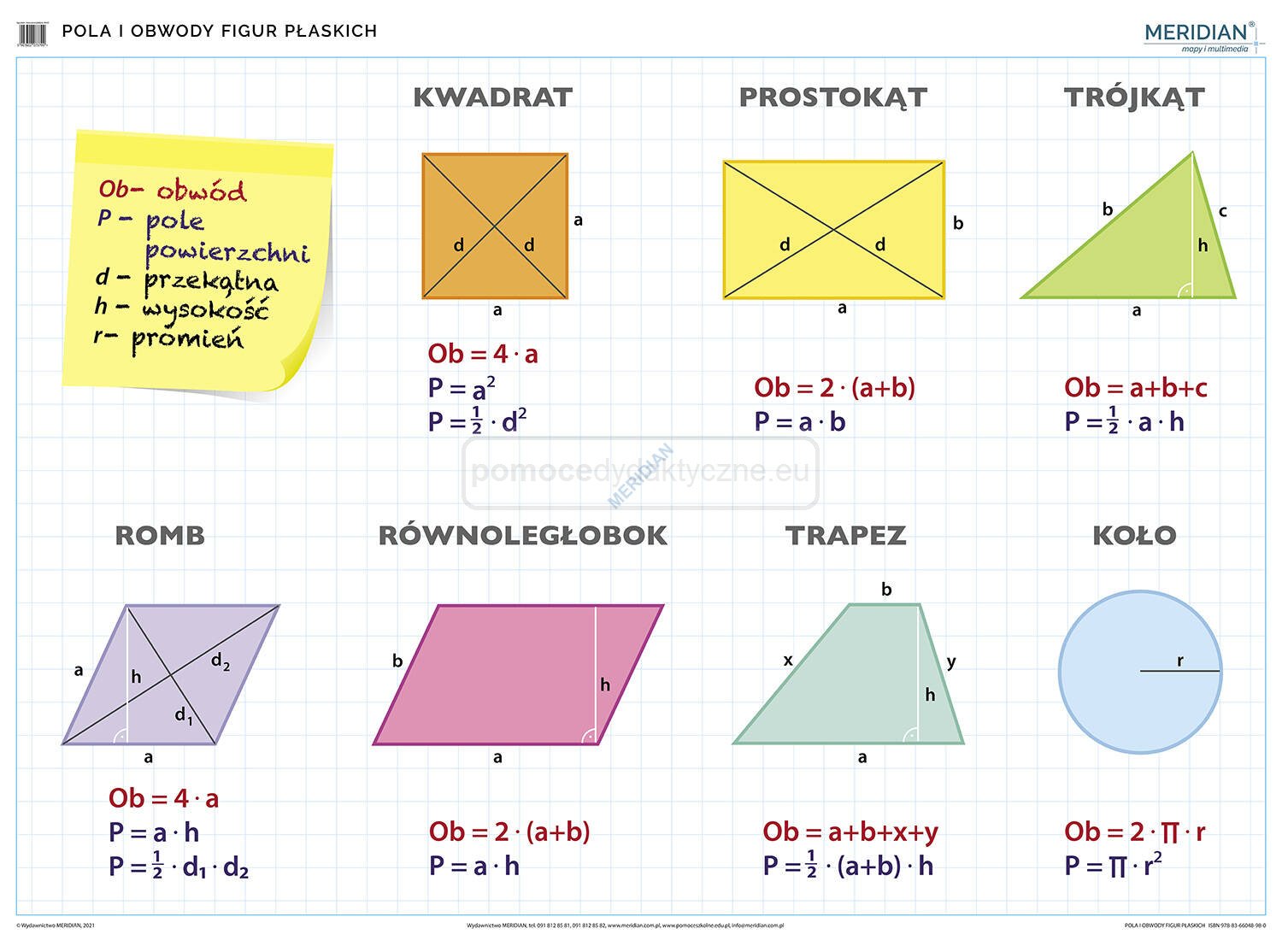
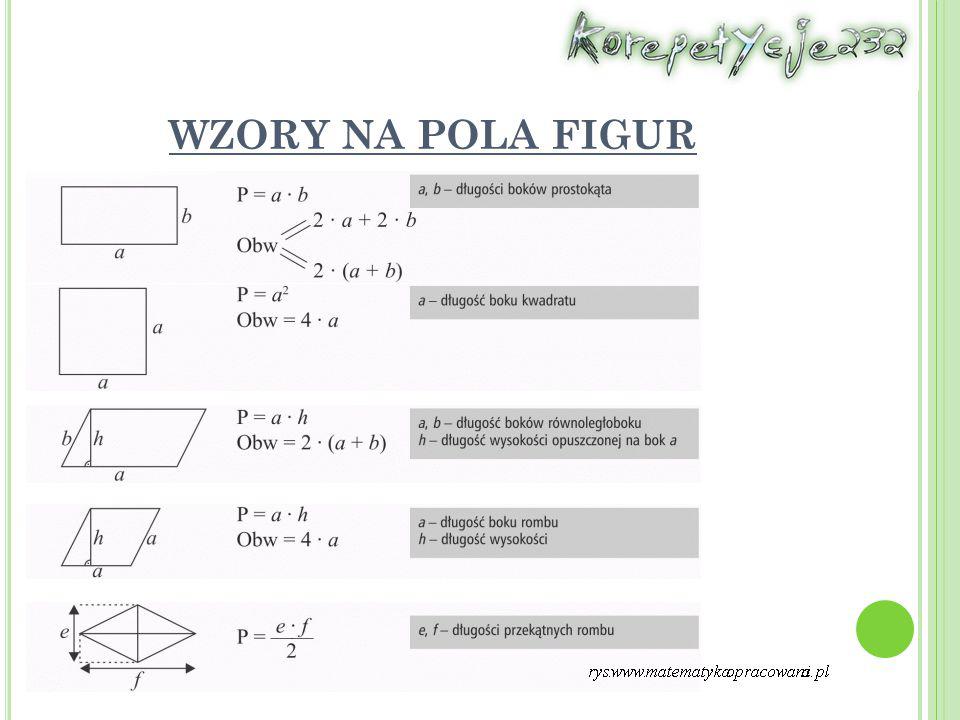
Kwadrat

Kwadrat to figura o czterech równych bokach i czterech kątach prostych. Jego pole obliczamy bardzo prosto:

Wzór: P = a², gdzie a to długość boku kwadratu.

Przykład: Jeśli bok kwadratu ma długość 5 cm, to jego pole wynosi P = 5² = 25 cm².

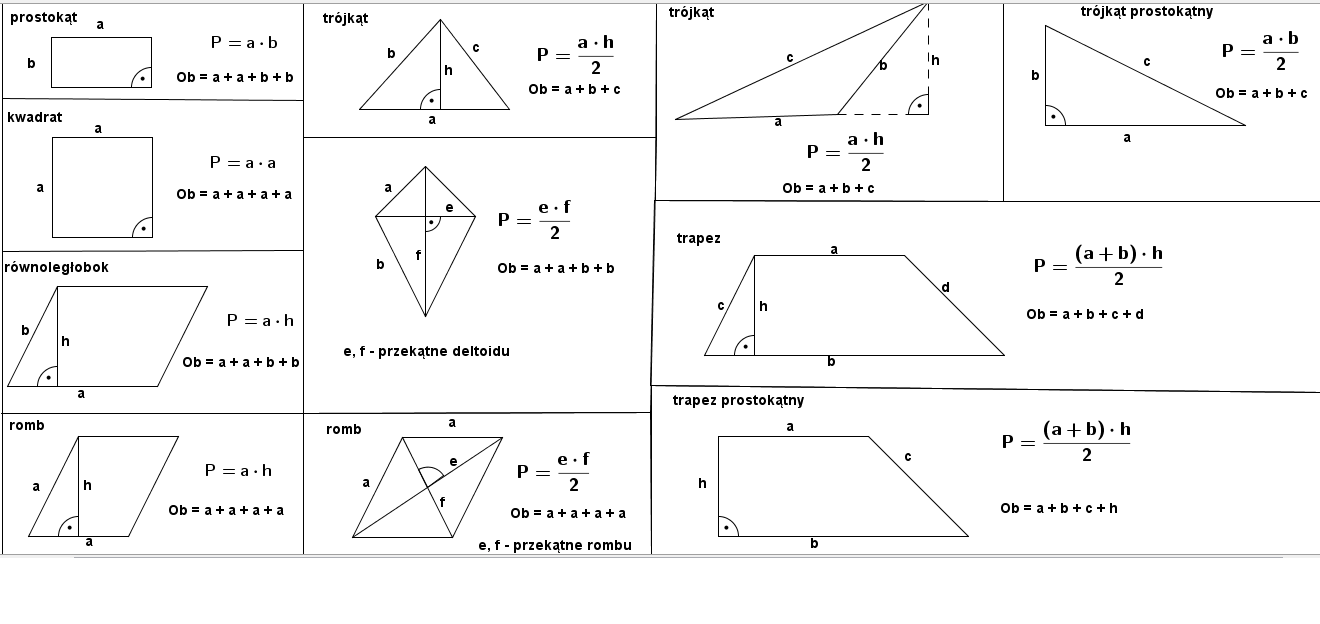
Prostokąt

Prostokąt, podobnie jak kwadrat, ma cztery kąty proste, ale jego boki nie muszą być równe. Ma on dwie pary boków o jednakowej długości.

Wzór: P = a * b, gdzie a to długość jednego boku, a b to długość drugiego boku.

Przykład: Jeśli jeden bok prostokąta ma długość 8 cm, a drugi 3 cm, to jego pole wynosi P = 8 * 3 = 24 cm².

Trójkąt

Trójkąt to figura o trzech bokach i trzech kątach. Istnieje kilka sposobów na obliczenie jego pola, w zależności od posiadanych danych.

Podstawa i wysokość: P = (a * h) / 2, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę.
Wzór Herona: Jeśli znamy długości wszystkich trzech boków (a, b, c), możemy użyć wzoru Herona:
- p = (a + b + c) / 2 (połowa obwodu)
- P = √(p * (p - a) * (p - b) * (p - c))

Przykład: Trójkąt ma podstawę o długości 6 cm i wysokość opuszczoną na tę podstawę o długości 4 cm. Jego pole wynosi P = (6 * 4) / 2 = 12 cm².

Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Jego pole obliczamy podobnie jak pole prostokąta, ale z uwzględnieniem wysokości.

Wzór: P = a * h, gdzie a to długość boku, a h to wysokość opuszczona na ten bok.

Przykład: Równoległobok ma bok o długości 10 cm i wysokość opuszczoną na ten bok o długości 5 cm. Jego pole wynosi P = 10 * 5 = 50 cm².

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych (zwanych podstawami).

Wzór: P = ((a + b) * h) / 2, gdzie a i b to długości podstaw, a h to wysokość trapezu (odległość między podstawami).

Przykład: Trapez ma podstawy o długościach 7 cm i 3 cm, a wysokość wynosi 4 cm. Jego pole wynosi P = ((7 + 3) * 4) / 2 = 20 cm².

Koło

Koło to zbiór punktów na płaszczyźnie, których odległość od danego punktu (środka) jest mniejsza lub równa danej odległości (promieniowi).

Wzór: P = π * r², gdzie π (pi) to stała matematyczna w przybliżeniu równa 3.14159, a r to promień koła.

Przykład: Koło ma promień o długości 4 cm. Jego pole wynosi P = π * 4² ≈ 3.14159 * 16 ≈ 50.27 cm².

Romb

Romb to równoległobok, którego wszystkie boki są równe. Posiada dwie pary kątów ostrych i rozwartych.

Wzory:

P = a * h, gdzie a to długość boku, a h to wysokość opuszczona na ten bok.
P = (d₁ * d₂) / 2, gdzie d₁ i d₂ to długości przekątnych.

Przykład: Romb ma bok o długości 5 cm i wysokość opuszczoną na ten bok o długości 4 cm. Jego pole wynosi P = 5 * 4 = 20 cm². Alternatywnie, jeśli przekątne rombu mają długości 6 cm i 8 cm, to jego pole wynosi P = (6 * 8) / 2 = 24 cm².

Figury złożone – jak obliczyć ich pola?

Czasami mamy do czynienia z figurami, które nie są typowymi kwadratami, trójkątami czy kołami. Takie figury nazywamy figurami złożonymi. Jak obliczyć ich pola?

Najprostszym sposobem jest rozłożenie figury złożonej na mniejsze, prostsze figury, których pola potrafimy obliczyć. Następnie sumujemy pola tych mniejszych figur, aby otrzymać pole figury złożonej.

Przykład: Wyobraź sobie, że masz figurę w kształcie litery "L". Możesz ją podzielić na dwa prostokąty. Oblicz pole każdego prostokąta osobno, a następnie zsumuj te pola, aby otrzymać pole całej figury "L".

Inną metodą jest odejmowanie pól. Jeśli figura złożona powstaje przez usunięcie jednej figury z drugiej, to obliczamy pola obu figur i odejmujemy pole mniejszej figury od pola większej.

Przykład: Wyobraź sobie kwadrat z wyciętym w środku kołem. Aby obliczyć pole takiej figury, obliczamy pole kwadratu i pole koła, a następnie odejmujemy pole koła od pola kwadratu.

Praktyczne zastosowania wzorów na pola figur

Wzory na pola figur geometrycznych mają niezliczone zastosowania w życiu codziennym i w różnych dziedzinach nauki i techniki.

Budownictwo i architektura: Obliczanie ilości materiałów potrzebnych do budowy domu, wyznaczanie powierzchni ścian, podłóg i dachów.
Rolnictwo: Obliczanie powierzchni pól uprawnych, szacowanie plonów.
Inżynieria: Projektowanie mostów, budynków i innych konstrukcji.
Geodezja: Pomiar powierzchni działek i gruntów.
Sztuka i rzemiosło: Obliczanie ilości materiałów potrzebnych do wykonania obrazu, haftu czy rzeźby.
Krawiectwo: Obliczanie ilości materiału potrzebnego do uszycia ubrania.
Gotowanie: Określanie wielkości blachy do pieczenia ciasta.

Przykład: Remontujesz pokój i chcesz pomalować ściany. Musisz najpierw obliczyć powierzchnię ścian, aby wiedzieć, ile farby potrzebujesz. Wzory na pola prostokątów i kwadratów okażą się tutaj niezwykle przydatne!

Wskazówki i triki

Obliczanie pól figur może być łatwiejsze, jeśli zapamiętasz kilka przydatnych wskazówek:

Zawsze używaj odpowiednich jednostek miary. Jeśli długości boków podane są w centymetrach, to pole będzie wyrażone w centymetrach kwadratowych.
Dokładnie analizuj rysunek. Upewnij się, że dobrze rozumiesz, które wartości odpowiadają długościom boków, wysokościom czy promieniom.
Jeśli masz wątpliwości, rozłóż figurę złożoną na prostsze. To zawsze dobry sposób na uproszczenie problemu.
Sprawdzaj swoje obliczenia. Upewnij się, że nie popełniłeś błędów.
Korzystaj z kalkulatora. Szczególnie przy obliczeniach z użyciem liczby π lub wzoru Herona.

Podsumowanie

Znajomość wzorów na pola figur geometrycznych to nieoceniona umiejętność, która przydaje się w wielu aspektach życia. Od prostych obliczeń związanych z remontem domu po bardziej zaawansowane zadania inżynieryjne – te wzory są fundamentem wielu dziedzin.

Mamy nadzieję, że ten artykuł był dla Ciebie pomocny i pozwolił Ci odświeżyć lub uzupełnić swoją wiedzę z geometrii. Pamiętaj, że praktyka czyni mistrza, więc ćwicz obliczanie pól różnych figur, a staniesz się w tym coraz lepszy!

Teraz to Twoja kolej! Wykorzystaj zdobytą wiedzę w praktyce i rozwiąż kilka zadań. Zobaczysz, jak satysfakcjonujące może być obliczanie pól figur!