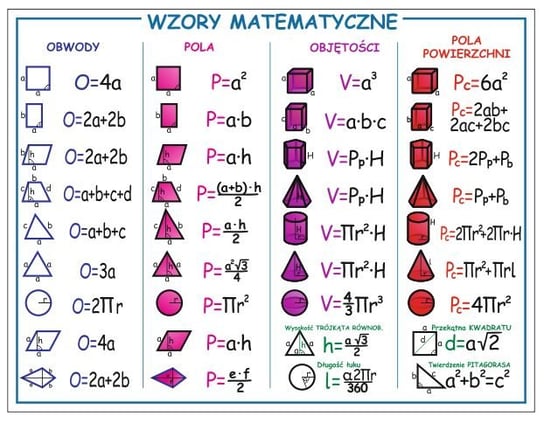
Wszystkie Wzory Matematyczne Klasa 8

Witaj w przewodniku po wszystkich wzorach matematycznych dla klasy 8! Matematyka w ósmej klasie to naprawdę ekscytujący etap, gdzie narzędzia stają się bardziej zaawansowane, a problemy – ciekawsze. Pomyśl o tym jak o budowie solidnego domu. Każdy wzór to cegła lub deska, która musi być prawidłowo osadzona, by cała konstrukcja była stabilna. Gotowy? Zaczynamy!

Pierwiastki Kwadratowe i Sześcienne

Zacznijmy od czegoś, co na początku może wydawać się skomplikowane, ale z odpowiednim podejściem staje się proste jak 1, 2, 3! Mówimy o pierwiastkach kwadratowych i sześciennych.

Pierwiastek Kwadratowy

Co to w ogóle jest? Wyobraź sobie, że masz kwadrat o polu powierzchni 9. Jak długa jest jego bok? To właśnie pierwiastek kwadratowy z 9, czyli 3! Pierwiastek kwadratowy z liczby "a" to liczba, która pomnożona przez samą siebie daje "a". Oznaczamy to symbolem: √a.

Przykłady:

√4 = 2 (bo 2 * 2 = 4)
√25 = 5 (bo 5 * 5 = 25)
√100 = 10 (bo 10 * 10 = 100)

Ważna uwaga: Nie możemy wyciągnąć pierwiastka kwadratowego z liczby ujemnej (w zbiorze liczb rzeczywistych). Spróbuj pomnożyć jakąkolwiek liczbę przez samą siebie – zawsze otrzymasz liczbę dodatnią lub zero.

Działania na pierwiastkach:

√(a * b) = √a * √b (Pierwiastek z iloczynu to iloczyn pierwiastków)
√(a / b) = √a / √b (Pierwiastek z ilorazu to iloraz pierwiastków)

Przykład praktyczny: Chcesz obliczyć powierzchnię kwadratowego placu zabaw, którego bok ma długość √16 metrów. Długość boku to √16 = 4 metry. Powierzchnia to bok * bok = 4 * 4 = 16 metrów kwadratowych.

Pierwiastek Sześcienny

Podobna idea, ale teraz myślimy o sześcianie! Jeśli masz sześcian o objętości 8, jak długa jest jego krawędź? To pierwiastek sześcienny z 8, czyli 2! Pierwiastek sześcienny z liczby "a" to liczba, która pomnożona przez samą siebie TRZY RAZY daje "a". Oznaczamy to symbolem: ∛a.

Przykłady:

∛8 = 2 (bo 2 * 2 * 2 = 8)
∛27 = 3 (bo 3 * 3 * 3 = 27)
∛125 = 5 (bo 5 * 5 * 5 = 125)

Ciekawostka: Możemy wyciągnąć pierwiastek sześcienny z liczb ujemnych! Np. ∛(-8) = -2 (bo -2 * -2 * -2 = -8).

Działania na pierwiastkach sześciennych:

∛(a * b) = ∛a * ∛b
∛(a / b) = ∛a / ∛b

Przykład praktyczny: Chcesz zbudować kostkę z klocków o objętości 64 cm³. Jaką długość musi mieć bok kostki? Długość boku to ∛64 = 4 cm.

Wzory Skróconego Mnożenia

Te wzory to takie "triki", które pozwalają szybciej rozwiązywać pewne typy zadań. Pomyśl o nich jak o skrótach na mapie – zamiast jechać okrężną drogą, możesz użyć skrótu i dotrzeć do celu szybciej!

Kwadrat Sumy: (a + b)² = a² + 2ab + b²

Wyobraź sobie kwadrat o boku (a + b). Możesz go podzielić na mniejsze kwadraty o bokach "a" i "b" oraz dwa prostokąty o bokach "a" i "b". Pole całego kwadratu to suma pól tych mniejszych figur: a² + 2ab + b².

Przykład: (x + 3)² = x² + 2 * x * 3 + 3² = x² + 6x + 9

Kwadrat Różnicy: (a - b)² = a² - 2ab + b²

Podobnie, ale teraz odejmujemy! Możesz wizualizować to jako kwadrat o boku "a", z którego wycinamy mniejszy kwadrat o boku "b".

Przykład: (y - 2)² = y² - 2 * y * 2 + 2² = y² - 4y + 4

Różnica Kwadratów: a² - b² = (a + b)(a - b)

To chyba najfajniejszy wzór! Można go wizualizować jako duży kwadrat o boku "a", z którego wycięto mniejszy kwadrat o boku "b". Pozostałą powierzchnię można przekształcić w prostokąt o bokach (a + b) i (a - b).

Przykład: x² - 16 = (x + 4)(x - 4)

Suma Sześcianów: a³ + b³ = (a + b)(a² - ab + b²)

To rozszerzenie idei z różnicy kwadratów na sześciany. Wizualizacja tego jest trudniejsza, ale wzór jest potężny!

Przykład: x³ + 8 = (x + 2)(x² - 2x + 4)

Różnica Sześcianów: a³ - b³ = (a - b)(a² + ab + b²)

Podobny do sumy sześcianów, ale z drobnymi zmianami w znakach.

Przykład: x³ - 27 = (x - 3)(x² + 3x + 9)

Geometria

Geometria to wizualna strona matematyki! Pamiętaj, że rysunek często pomaga zrozumieć problem.

Twierdzenie Pitagorasa: a² + b² = c²

To absolutna podstawa! Dotyczy trójkątów prostokątnych, gdzie "a" i "b" to długości przyprostokątnych (boków przylegających do kąta prostego), a "c" to długość przeciwprostokątnej (najdłuższy bok, leżący naprzeciwko kąta prostego). Wyobraź sobie kwadraty zbudowane na każdym z boków trójkąta prostokątnego. Pole kwadratu zbudowanego na przeciwprostokątnej jest równe sumie pól kwadratów zbudowanych na przyprostokątnych.

Przykład: Jeśli a = 3, b = 4, to c² = 3² + 4² = 9 + 16 = 25, więc c = √25 = 5.

Wzory na Pola i Obwody Figur

Pamiętaj o jednostkach! Pole podajemy w jednostkach kwadratowych (np. cm²), a obwód w jednostkach długości (np. cm).

Kwadrat: Pole = a², Obwód = 4a (gdzie "a" to długość boku)
Prostokąt: Pole = a * b, Obwód = 2a + 2b (gdzie "a" i "b" to długości boków)
Trójkąt: Pole = (1/2) * a * h (gdzie "a" to długość podstawy, a "h" to wysokość opuszczona na tę podstawę), Obwód = a + b + c (gdzie "a", "b", "c" to długości boków)
Równoległobok: Pole = a * h, Obwód = 2a + 2b (gdzie "a" to długość podstawy, "h" to wysokość opuszczona na tę podstawę, "b" to długość drugiego boku)
Trapez: Pole = (1/2) * (a + b) * h (gdzie "a" i "b" to długości podstaw, a "h" to wysokość)
Koło: Pole = πr², Obwód (długość okręgu) = 2πr (gdzie "r" to promień koła, a π (pi) ≈ 3.14)

Pamiętaj, by zawsze rysować sobie te figury! To bardzo pomaga w zrozumieniu wzorów i w rozwiązywaniu zadań.

Podsumowanie

To jest spory kawałek wiedzy, ale pamiętaj: praktyka czyni mistrza! Im więcej będziesz ćwiczyć i rozwiązywać zadań, tym lepiej zapamiętasz te wzory i tym łatwiej będzie Ci je stosować. Pomyśl o tym jak o nauce jazdy na rowerze – na początku jest trudno, ale z czasem staje się to naturalne. Nie zrażaj się trudnościami, pytaj nauczyciela lub kolegów, korzystaj z internetu (ale z głową!) i przede wszystkim – baw się dobrze matematyką!

Powodzenia!