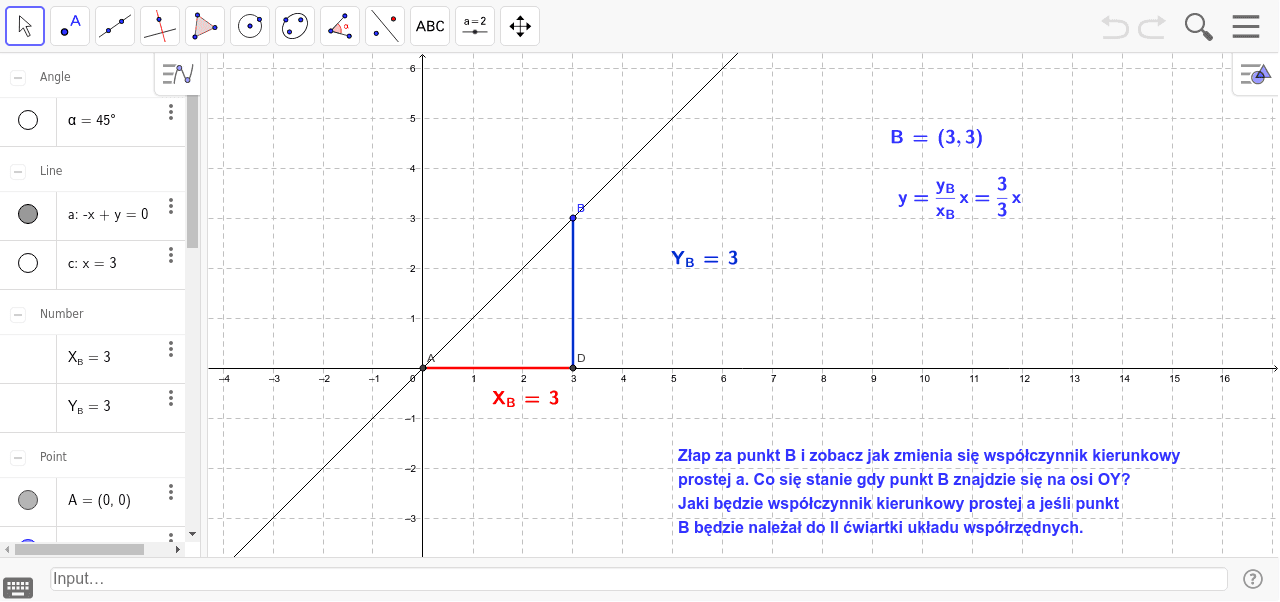
Współczynnik Kierunkowy Prostej Przechodzącej Przez Punkty

Okej, spróbujmy wytłumaczyć, jak obliczyć współczynnik kierunkowy prostej przechodzącej przez dwa punkty w sposób prosty i zrozumiały.

Załóżmy, że mamy dwa punkty na płaszczyźnie: punkt A o współrzędnych (x₁, y₁) oraz punkt B o współrzędnych (x₂, y₂). Naszym celem jest znalezienie współczynnika kierunkowego prostej, która przechodzi przez oba te punkty. Ten współczynnik, często oznaczany literą 'a' lub 'm', mówi nam, jak bardzo "stromo" wznosi się lub opada ta prosta. Innymi słowy, informuje nas, o ile zmienia się wartość y, gdy wartość x zmienia się o jednostkę.

Aby to obliczyć, potrzebujemy wzoru:

a = (y₂ - y₁) / (x₂ - x₁)

Spróbujmy przeanalizować to krok po kroku na konkretnych przykładach.

Przykład 1:

Załóżmy, że punkt A ma współrzędne (1, 2), a punkt B ma współrzędne (4, 8). Chcemy znaleźć współczynnik kierunkowy prostej, która przechodzi przez te dwa punkty.

1. Oznaczmy współrzędne:

   • x₁ = 1
   • y₁ = 2
   • x₂ = 4
   • y₂ = 8

2. Podstawmy te wartości do wzoru: a = (8 - 2) / (4 - 1)

3. Wykonajmy odejmowanie: a = 6 / 3

4. Wykonajmy dzielenie: a = 2

Współczynnik kierunkowy tej prostej wynosi 2. Oznacza to, że gdy x wzrasta o 1, y wzrasta o 2. Prosta wznosi się.

Przykład 2:

Powiedzmy, że punkt A ma współrzędne (-2, 3), a punkt B ma współrzędne (1, -3). Znów chcemy obliczyć współczynnik kierunkowy.

1. Oznaczmy współrzędne:

   • x₁ = -2
   • y₁ = 3
   • x₂ = 1
   • y₂ = -3

2. Podstawmy do wzoru: a = (-3 - 3) / (1 - (-2))

3. Wykonajmy odejmowanie (pamiętajmy o minusach!): a = -6 / 3

4. Wykonajmy dzielenie: a = -2

Współczynnik kierunkowy wynosi -2. Oznacza to, że gdy x wzrasta o 1, y maleje o 2. Prosta opada.

Przykład 3:

Punkt A ma współrzędne (5, 1), a punkt B ma współrzędne (5, 7).

1. Oznaczmy współrzędne:

   • x₁ = 5
   • y₁ = 1
   • x₂ = 5
   • y₂ = 7

2. Podstawmy do wzoru: a = (7 - 1) / (5 - 5)

3. Wykonajmy odejmowanie: a = 6 / 0

Ups! Dzielenie przez zero jest niedozwolone. Co to oznacza? Oznacza to, że prosta jest pionowa. Prosta pionowa nie ma określonego współczynnika kierunkowego. Mówimy, że jej współczynnik kierunkowy jest "nieokreślony". Wszystkie punkty na tej prostej mają taką samą współrzędną x.

Przykład 4:

Punkt A ma współrzędne (2, 4), a punkt B ma współrzędne (6, 4).

1. Oznaczmy:

   • x₁ = 2
   • y₁ = 4
   • x₂ = 6
   • y₂ = 4

2. Podstawiamy: a = (4 - 4) / (6 - 2)

3. Obliczamy: a = 0 / 4

4. Wynik: a = 0

Kiedy współczynnik kierunkowy jest równy 0, oznacza to, że prosta jest pozioma. Wartość y nie zmienia się, niezależnie od wartości x. Wszystkie punkty na tej prostej mają tę samą współrzędną y.

Kiedy Zamieniać Punkty?

Czy ma znaczenie, który punkt nazwiemy A, a który B? Otóż nie. Ważne jest tylko, żeby konsekwentnie używać tych oznaczeń we wzorze. Możemy równie dobrze obliczyć współczynnik kierunkowy, zamieniając punkty A i B.

Przykład:

Weźmy ponownie punkt A (1, 2) i punkt B (4, 8). Obliczyliśmy wcześniej, że a = 2. Teraz zamieńmy punkty i zobaczmy, co się stanie.

Teraz:

• x₁ = 4
• y₁ = 8
• x₂ = 1
• y₂ = 2

Podstawmy do wzoru: a = (2 - 8) / (1 - 4) a = -6 / -3 a = 2

Otrzymaliśmy ten sam wynik!

Jak Unikać Błędów?

Najczęstszym błędem jest pomylenie kolejności odejmowania. Pamiętaj, że musisz odjąć współrzędne y w tej samej kolejności, co współrzędne x. Jeśli odejmujesz y₂ - y₁, to musisz również odjąć x₂ - x₁. Odjęcie w odwrotnej kolejności da ci wynik o przeciwnym znaku (co jest błędem, chyba że zamienisz kolejność odejmowania zarówno w liczniku, jak i mianowniku, jak widzieliśmy wcześniej).

Innym częstym błędem są błędy w obliczeniach, zwłaszcza przy operowaniu na liczbach ujemnych. Dlatego zawsze warto wykonywać obliczenia krok po kroku i sprawdzać, czy nie popełniliśmy gdzieś błędu.

Na koniec, pamiętaj o przypadkach szczególnych: prosta pionowa (dzielenie przez zero) i prosta pozioma (współczynnik kierunkowy równy zero). Zawsze warto wizualizować sobie, jak wygląda prosta przechodząca przez dane punkty. Pomoże to zidentyfikować ewentualne błędy w obliczeniach.

Mamy nadzieję, że to wyjaśnienie jest pomocne! Jeśli masz jakieś pytania, nie wahaj się pytać. Powodzenia w obliczaniu współczynników kierunkowych!