Własności Trójkata 90 60 30

W świecie geometrii, trójkąty stanowią fundament wielu konstrukcji i obliczeń. Wśród nich, szczególne miejsce zajmuje trójkąt prostokątny o kątach 90°, 60° i 30°. Jego unikalne właściwości sprawiają, że jest niezwykle przydatny w różnych dziedzinach, od matematyki i fizyki, po inżynierię i architekturę. W tym artykule przyjrzymy się bliżej charakterystycznym cechom tego fascynującego kształtu, zbadamy jego relacje boków i zastosowania w praktyce.

Właściwości Kątów i Boków

Najważniejszą cechą trójkąta 90-60-30 jest oczywiście jego zestaw kątów: prosty (90°), ostry (60°) i ostry (30°). Suma kątów w każdym trójkącie wynosi 180°, co czyni ten podział wyjątkowo harmonijnym. To, co jednak czyni go szczególnie interesującym, to specyficzne proporcje między długościami jego boków. Te proporcje są stałe i wynikają z własności trójkątów podobnych.

Zależności Między Bokami

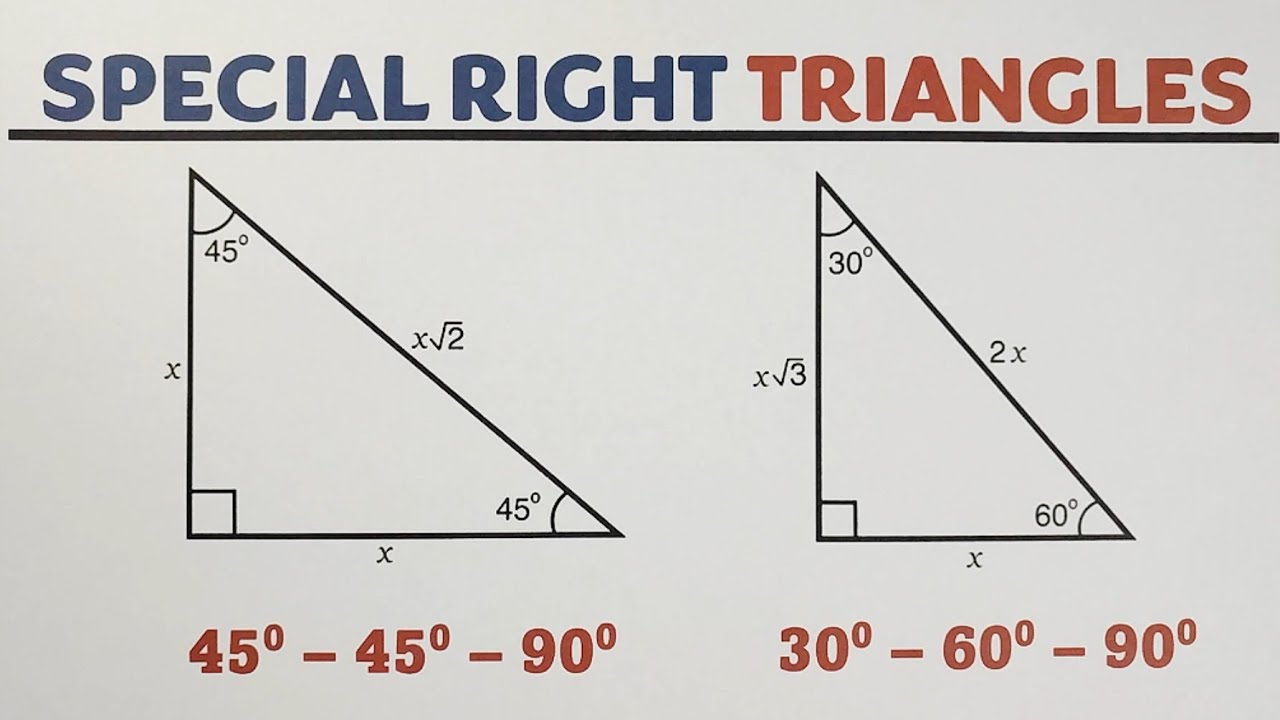
W trójkącie prostokątnym 90-60-30 istnieje prosta i niezmienna zależność między długościami boków. Oznaczmy:

a – długość boku naprzeciwko kąta 30° (krótsza przyprostokątna)
b – długość boku naprzeciwko kąta 60° (dłuższa przyprostokątna)
c – długość przeciwprostokątnej (bok naprzeciwko kąta 90°)

Wtedy:

c = 2a (Przeciwprostokątna jest dwa razy dłuższa niż krótsza przyprostokątna)
b = a√3 (Dłuższa przyprostokątna jest równa krótszej przyprostokątnej pomnożonej przez pierwiastek z 3)

Te zależności są fundamentalne i pozwalają na szybkie obliczanie długości boków, znając tylko jeden z nich. Dzięki nim, nie musimy za każdym razem odwoływać się do bardziej skomplikowanych narzędzi, jak twierdzenie Pitagorasa (choć oczywiście, jest ono w tym przypadku jak najbardziej poprawne i może służyć do weryfikacji wyników).

Dowód Zależności Boków

Zależności te wynikają z właściwości trójkąta równobocznego. Rozważmy trójkąt równoboczny o boku długości 2a. Jeśli przetniemy go na pół, prowadząc wysokość z jednego wierzchołka na środek przeciwległego boku, otrzymamy dwa identyczne trójkąty prostokątne 90-60-30. Wysokość ta jest jednocześnie środkową i dwusieczną kąta. Krótsza przyprostokątna powstałego trójkąta (bok a) jest połową boku trójkąta równobocznego, przeciwprostokątna (bok c) ma długość boku trójkąta równobocznego (2a), a dłuższa przyprostokątna (bok b) jest wysokością trójkąta równobocznego. Z twierdzenia Pitagorasa dla trójkąta równobocznego o boku 2a, obliczamy wysokość: b = √(4a² - a²) = √(3a²) = a√3. To dowodzi, że b = a√3.

Praktyczne Zastosowania

Właściwości trójkąta 90-60-30 znajdują szerokie zastosowanie w różnych dziedzinach. Oto kilka przykładów:

Architektura i Budownictwo

W architekturze i budownictwie, trójkąty 90-60-30 są wykorzystywane do projektowania dachów, schodów i innych elementów konstrukcyjnych. Znając kąt nachylenia dachu (często 30° lub 60°), można łatwo obliczyć długość krokwi, wysokość ściany szczytowej i inne parametry. Na przykład, konstruując dach o kącie nachylenia 30°, architekt wie, że wysokość dachu będzie połową długości krokwi (przy założeniu, że krokwie zaczynają się od poziomu fundamentu). To upraszcza obliczenia i przyspiesza proces projektowania.

Nawigacja i Geodezja

W nawigacji i geodezji, trójkąty 90-60-30 mogą być używane do określania odległości i wysokości. Wykorzystując techniki triangulacji, można wyznaczyć położenie punktu na podstawie pomiarów kątów i odległości do innych znanych punktów. Znając kąt wzniesienia do szczytu góry i odległość od obserwatora do podstawy góry, można obliczyć wysokość góry. Historycznie, przed erą GPS, tego typu obliczenia były kluczowe dla tworzenia map i nawigacji morskiej.

Inżynieria

W inżynierii, trójkąty 90-60-30 znajdują zastosowanie w projektowaniu maszyn i urządzeń. Na przykład, w mechanizmach dźwigniowych i przekładniach zębatych, odpowiednie kąty i proporcje mogą zapewnić optymalną wydajność i siłę. Analiza sił działających na elementy konstrukcyjne często sprowadza się do rozkładu wektorów na składowe, a trójkąt 90-60-30 może ułatwić te obliczenia, szczególnie w sytuacjach, gdy siły działają pod kątem 30° lub 60° względem siebie.

Matematyka i Fizyka

W matematyce i fizyce, trójkąt 90-60-30 jest cennym narzędziem do rozwiązywania problemów geometrycznych i trygonometrycznych. Umożliwia on łatwe wyprowadzanie wartości funkcji trygonometrycznych dla kątów 30° i 60° (sinus, cosinus, tangens). Znając te wartości, można rozwiązywać równania trygonometryczne i analizować ruch harmoniczny prosty. Ponadto, trójkąt ten jest często używany jako przykład w zadaniach z geometrii, pomagając studentom zrozumieć zasady podobieństwa trójkątów i twierdzenia Pitagorasa.

Przykłady liczbowe

Przykład 1: Załóżmy, że krótsza przyprostokątna trójkąta 90-60-30 ma długość 5 cm (a=5 cm). Wtedy:

Dłuższa przyprostokątna: b = 5√3 cm ≈ 8.66 cm
Przeciwprostokątna: c = 2 * 5 cm = 10 cm

Przykład 2: Mamy przeciwprostokątną o długości 12 m (c = 12 m). Wtedy:

Krótsza przyprostokątna: a = 12 m / 2 = 6 m
Dłuższa przyprostokątna: b = 6√3 m ≈ 10.39 m

Przykład 3: Znana jest dłuższa przyprostokątna i ma długość 7√3 dm (b = 7√3 dm). Wtedy:

Krótsza przyprostokątna: a = 7√3 dm / √3 = 7 dm
Przeciwprostokątna: c = 2 * 7 dm = 14 dm

Podsumowanie

Trójkąt prostokątny o kątach 90°, 60° i 30° to wyjątkowy kształt geometryczny o wielu przydatnych właściwościach. Jego proste i niezmienne zależności między bokami sprawiają, że jest on łatwy w użyciu i znajduje szerokie zastosowanie w różnych dziedzinach. Od architektury i budownictwa, po nawigację, inżynierię, matematykę i fizykę, trójkąt 90-60-30 stanowi cenne narzędzie dla inżynierów, naukowców i matematyków.

Zachęcamy do praktycznego wykorzystania wiedzy na temat trójkąta 90-60-30 w rozwiązywaniu problemów geometrycznych i konstrukcyjnych. Im więcej będziemy z nim pracować, tym lepiej zrozumiemy jego potencjał i docenimy jego prostotę i elegancję.