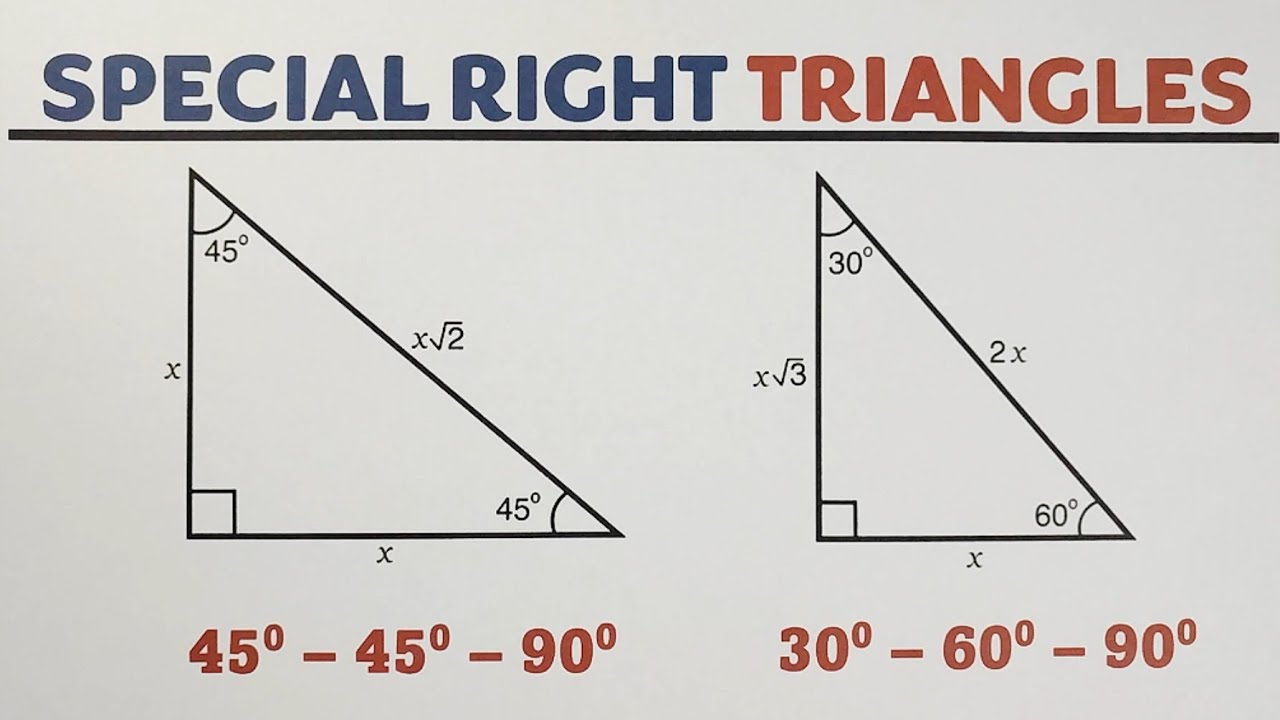
Własności Trójkąta 45 45 90

Zmagasz się z geometrią? A może masz wrażenie, że pewne figury geometryczne, jak trójkąt 45 45 90, to czarna magia? Spokojnie, wielu uczniów (i nie tylko!) ma podobne odczucia. Kluczem do sukcesu jest zrozumienie podstawowych własności i umiejętność ich praktycznego zastosowania. Ten artykuł rozwieje Twoje wątpliwości i pokaże, że geometria wcale nie musi być straszna! Zamiast ślęczeć nad książkami bez zrozumienia, dowiedz się jak efektywnie wykorzystywać wiedzę o trójkącie prostokątnym równoramiennym.

Wprowadzenie do trójkąta 45 45 90

Zacznijmy od podstaw. Trójkąt 45 45 90, jak sama nazwa wskazuje, charakteryzuje się specyficznymi kątami: 45 stopni, 45 stopni i 90 stopni. Jest to trójkąt prostokątny, co oznacza, że jeden z jego kątów jest kątem prostym (90 stopni). Dodatkowo, jest to trójkąt równoramienny, czyli posiada dwa boki o tej samej długości.

Dlaczego ta figura jest tak ważna? Ponieważ bardzo często pojawia się w zadaniach geometrycznych, w życiu codziennym (np. w konstrukcji kwadratu) oraz posiada proste i eleganckie zależności między długościami boków, co ułatwia obliczenia.

Podstawowe własności i zależności

Najważniejsza rzecz, którą musisz zapamiętać, to zależność między długościami boków trójkąta 45 45 90. Oznaczmy długość każdego z równych boków (przyprostokątnych) jako "a". Wtedy długość przeciwprostokątnej (najdłuższego boku, naprzeciw kąta prostego) wynosi a√2. Czyli:

Przyprostokątna: a
Przyprostokątna: a
Przeciwprostokątna: a√2

Ta prosta formuła to klucz do rozwiązania wielu zadań! Zapamiętaj ją dobrze.

Przykład: Jeśli przyprostokątna trójkąta 45 45 90 ma długość 5 cm, to przeciwprostokątna ma długość 5√2 cm. Proste, prawda?

Dowód zależności boków

Skąd się bierze ta zależność? Możemy ją łatwo udowodnić, korzystając z twierdzenia Pitagorasa. W trójkącie prostokątnym, suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Czyli:

a² + a² = c²

Gdzie 'a' to długość przyprostokątnej, a 'c' to długość przeciwprostokątnej.

Upraszczając:

2a² = c²

Wyciągając pierwiastek kwadratowy z obu stron:

√(2a²) = √c²

a√2 = c

I voilà! Udowodniliśmy, że przeciwprostokątna ma długość a√2.

Praktyczne zastosowania trójkąta 45 45 90

Ok, znamy teorię, ale jak to wykorzystać w praktyce? Oto kilka przykładów:

* **Obliczanie przekątnej kwadratu:** Przekątna kwadratu dzieli go na dwa trójkąty 45 45 90. Jeśli znasz długość boku kwadratu (a), to przekątna (c) wynosi a√2. Przykład: Kwadrat ma bok długości 10 cm. Jego przekątna ma długość 10√2 cm. * **Geodezja i miernictwo:** Trójkąty 45 45 90 są wykorzystywane do wyznaczania odległości i wysokości w terenie. * **Architektura i budownictwo:** Podczas projektowania i budowy konstrukcji, znajomość własności trójkąta 45 45 90 ułatwia obliczenia kątów i wymiarów. * **Zadania z geometrii:** Bardzo często w zadaniach maturalnych pojawiają się figury, które można rozłożyć na trójkąty 45 45 90. Rozpoznanie tego faktu znacznie ułatwia rozwiązanie.

Jak rozwiązywać zadania z trójkątem 45 45 90?

Oto kilka praktycznych wskazówek, które pomogą Ci w rozwiązywaniu zadań:

1. **Zidentyfikuj trójkąt:** Upewnij się, że masz do czynienia z trójkątem o kątach 45, 45 i 90 stopni. Czasami nie jest to podane wprost, ale wynika z danych zadania. 2. **Oznacz boki:** Oznacz długość przyprostokątnej jako "a". 3. **Wykorzystaj wzór:** Jeśli znasz długość przyprostokątnej, możesz obliczyć długość przeciwprostokątnej (a√2). Jeśli znasz długość przeciwprostokątnej, możesz obliczyć długość przyprostokątnej (c/√2). 4. **Uprość wynik:** Pamiętaj, żeby uprościć wynik, jeśli to możliwe. Na przykład, 4√8 można uprościć do 8√2. 5. **Sprawdź odpowiedź:** Zastanów się, czy uzyskany wynik jest sensowny w kontekście zadania. Czy długość przeciwprostokątnej jest na pewno większa niż długość przyprostokątnej?

Przykładowe zadanie

Zadanie: Oblicz pole trójkąta 45 45 90, jeśli jego przeciwprostokątna ma długość 8 cm.

Rozwiązanie:

Znamy długość przeciwprostokątnej (c = 8 cm).
Musimy obliczyć długość przyprostokątnej (a). Wiemy, że c = a√2, więc a = c/√2 = 8/√2.
Aby usunąć niewymierność z mianownika, mnożymy licznik i mianownik przez √2: a = (8√2)/2 = 4√2 cm.
Pole trójkąta (P) obliczamy ze wzoru: P = (a*a)/2 = (4√2 * 4√2)/2 = (16*2)/2 = 16 cm².

Odpowiedź: Pole trójkąta wynosi 16 cm².

Typowe błędy i jak ich unikać

Najczęstsze błędy popełniane podczas pracy z trójkątem 45 45 90 to:

* **Pomylenie wzoru:** Pamiętaj, że przeciwprostokątna to a√2, a nie odwrotnie. * **Zapominanie o twierdzeniu Pitagorasa:** Jeśli masz wątpliwości, zawsze możesz sprawdzić swoje obliczenia, korzystając z twierdzenia Pitagorasa. * **Brak upraszczania wyników:** Zawsze uprość swój wynik do najprostszej postaci. * **Niezrozumienie treści zadania:** Przeczytaj uważnie treść zadania i upewnij się, że rozumiesz, o co jesteś pytany.

Dodatkowe wskazówki

* **Rysuj schematy:** Nawet prosty szkic trójkąta z oznaczonymi długościami boków i kątami może bardzo pomóc w rozwiązaniu zadania. * **Ćwicz regularnie:** Im więcej zadań rozwiążesz, tym lepiej zrozumiesz własności trójkąta 45 45 90. * **Szukaj pomocy:** Jeśli masz trudności, nie krępuj się prosić o pomoc nauczyciela, kolegę lub skorzystaj z zasobów internetowych.

Podsumowanie

Trójkąt 45 45 90 to potężne narzędzie w geometrii. Zrozumienie jego własności i umiejętność ich praktycznego zastosowania znacznie ułatwi Ci rozwiązywanie zadań i zrozumienie wielu zagadnień matematycznych. Pamiętaj o zależnościach między bokami (a, a, a√2), twierdzeniu Pitagorasa i regularnych ćwiczeniach. Zastosuj te wskazówki, a geometria stanie się o wiele bardziej przystępna i zrozumiała! Powodzenia!