Wlasnosci Trojkata 30 60 90

Czy kiedykolwiek zastanawiałeś się, jak łatwo obliczyć długości boków w pewnych specyficznych trójkątach, znając tylko jeden z nich? Jeśli interesujesz się geometrią, matematyką, lub po prostu chcesz poszerzyć swoje umiejętności obliczeniowe, ten artykuł jest dla Ciebie! Przyjrzymy się bliżej trójkątowi o kątach 30, 60 i 90 stopni – figurze, która kryje w sobie niezwykłe właściwości i ułatwia wiele obliczeń.

Wprowadzenie do Trójkąta 30-60-90

Trójkąt 30-60-90 to nic innego jak trójkąt prostokątny, którego kąty wewnętrzne mają miary 30°, 60° i 90°. Ze względu na specyficzne proporcje między kątami, długości jego boków pozostają w stałej relacji. Ta relacja sprawia, że jest on niezwykle przydatny w rozwiązywaniu zadań geometrycznych, trygonometrycznych i inżynieryjnych.

Dlaczego Trójkąt 30-60-90 Jest Taki Wyjątkowy?

Unikalność trójkąta 30-60-90 wynika z jego związku z trójkątem równobocznym. Wyobraź sobie trójkąt równoboczny. Jeśli podzielimy go na pół wzdłuż wysokości, otrzymamy dwa identyczne trójkąty prostokątne o kątach 30, 60 i 90 stopni. To powiązanie jest kluczowe do zrozumienia proporcji między bokami.

Zależności Między Bokami Trójkąta 30-60-90

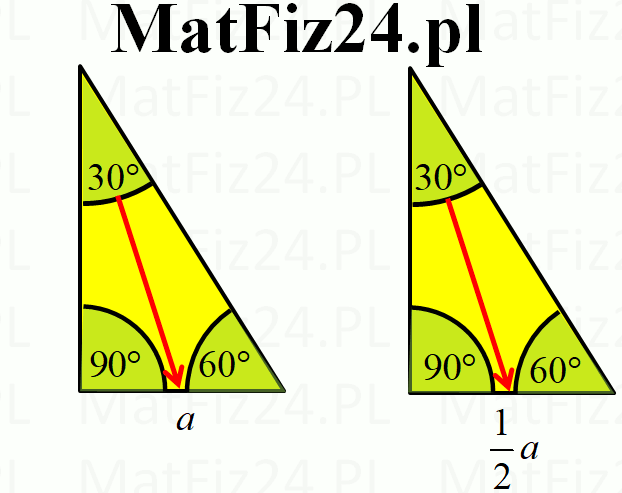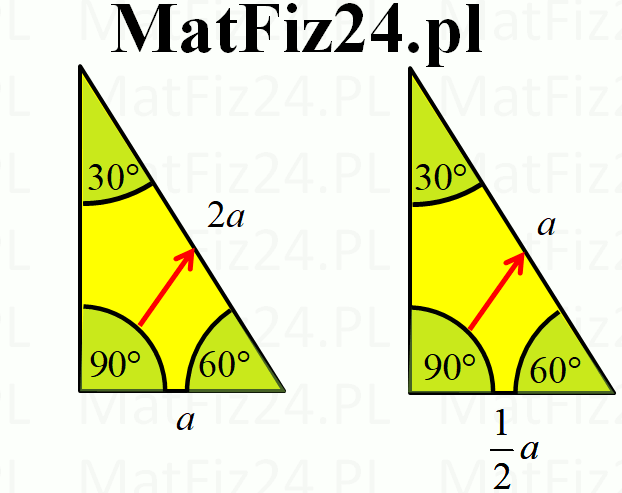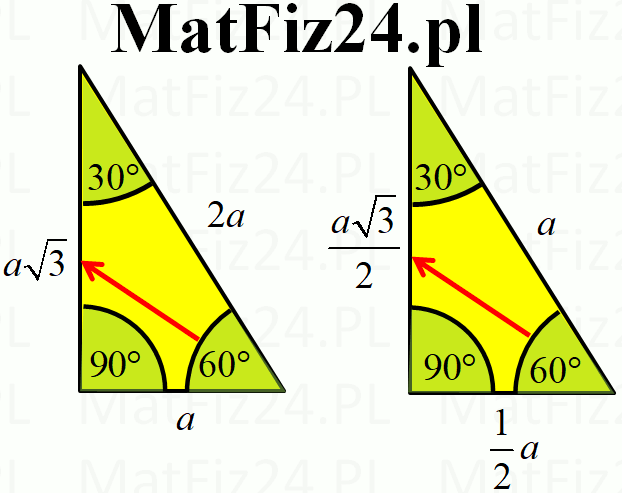
Najważniejsza zasada dotycząca trójkąta 30-60-90 to proporcje między długościami jego boków. Oznaczmy najkrótszy bok (leżący naprzeciw kąta 30°) jako 'a'. Wtedy:

Najkrótszy bok (naprzeciw kąta 30°): a
Bok średniej długości (naprzeciw kąta 60°): a√3
Przeciwprostokątna (naprzeciw kąta 90°): 2a

Te proporcje są niezmienne i prawdziwe dla każdego trójkąta o kątach 30, 60 i 90 stopni, niezależnie od jego wielkości. Znając długość jednego boku, możemy bez problemu obliczyć długości pozostałych.

Dowód Własności Trójkąta 30-60-90

Jak udowodnić te właściwości? Jak wspomniano wcześniej, punktem wyjścia jest trójkąt równoboczny. Załóżmy, że ma on bok długości 2a. Jego wysokość, która dzieli go na dwa trójkąty 30-60-90, dzieli podstawę na połowy, więc najkrótszy bok trójkąta 30-60-90 ma długość 'a'. Przeciwprostokątna trójkąta 30-60-90 to bok trójkąta równobocznego, czyli 2a. Długość boku naprzeciw kąta 60° możemy obliczyć z twierdzenia Pitagorasa:

(a)² + b² = (2a)²

a² + b² = 4a²

b² = 3a²

b = √(3a²) = a√3

Stąd, bok naprzeciw kąta 60° ma długość a√3.

Przykłady Zastosowania Własności Trójkąta 30-60-90

Zobaczmy, jak możemy wykorzystać te właściwości w praktyce:

Przykład 1: Obliczanie Wysokości Trójkąta Równobocznego

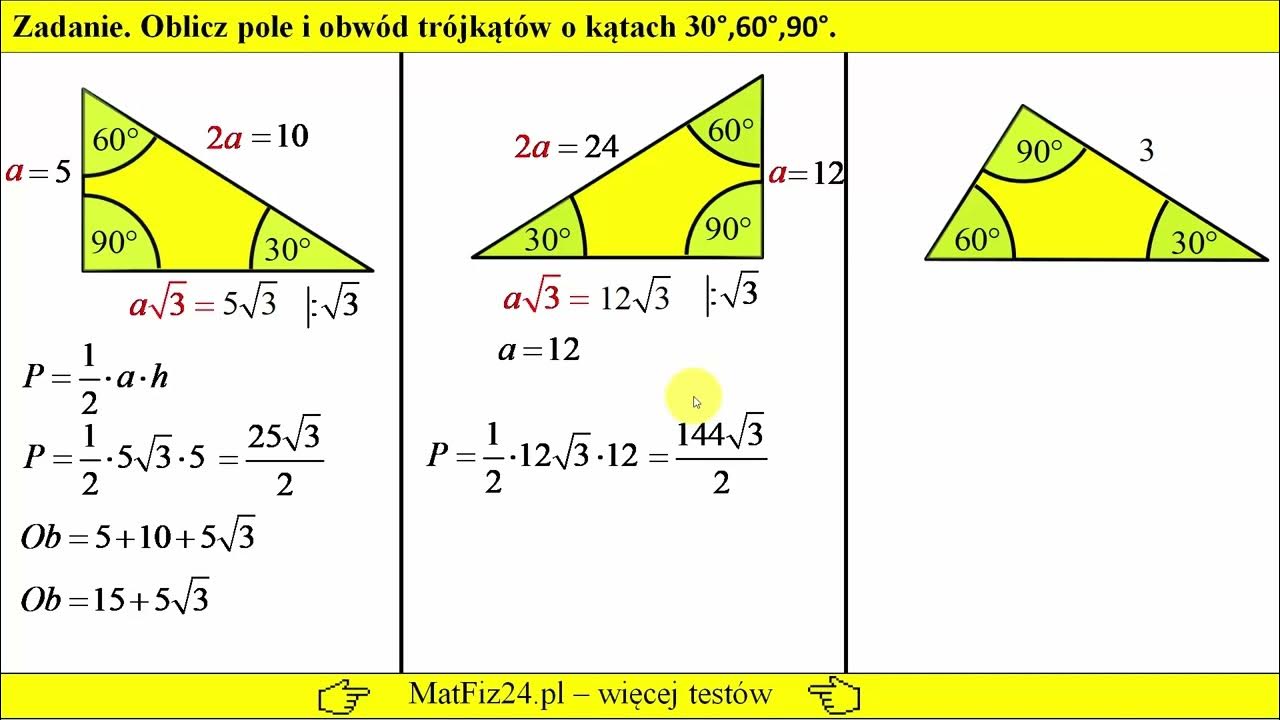
Mamy trójkąt równoboczny o boku długości 10 cm. Chcemy obliczyć jego wysokość. Jak wspomniano, wysokość dzieli trójkąt równoboczny na dwa trójkąty 30-60-90.

Rozwiązanie:

Przeciwprostokątna trójkąta 30-60-90 (bok trójkąta równobocznego) = 10 cm.
Zatem, '2a' = 10 cm, czyli 'a' = 5 cm (najkrótszy bok).
Wysokość trójkąta równobocznego to bok naprzeciw kąta 60°, czyli a√3 = 5√3 cm.

Przykład 2: Obliczanie Długości Boku Kwadratu Wpisanego w Okrąg

Kwadrat jest wpisany w okrąg o promieniu 4 cm. Oblicz długość boku kwadratu.

Rozwiązanie:

Przekątna kwadratu jest średnicą okręgu, czyli 2 * promień = 8 cm.
Przekątna kwadratu dzieli go na dwa trójkąty prostokątne równoramienne (czyli 45-45-90). Możemy także podzielić go na cztery trójkąty 30-60-90, łącząc środek okręgu z wierzchołkami kwadratu, a następnie rysując promienie prostopadłe do boków.
W takim przypadku, promień okręgu jest przeciwprostokątną trójkąta 30-60-90, czyli 2a = 4 cm, a więc a = 2 cm.
Bok kwadratu to dwa razy bok naprzeciw kąta 60°, czyli 2 * a√3 = 2 * 2√3 = 4√3 cm.

Przykład 3: Zadanie Praktyczne – Pochyłość Dachu

Projektant planuje dach, który ma tworzyć kąt 30 stopni z poziomem. Jeśli wysokość dachu (od legaru do kalenicy) ma wynosić 3 metry, jaką długość powinien mieć krokiew?

Rozwiązanie:

Wysokość dachu to bok naprzeciw kąta 30 stopni w trójkącie 30-60-90, czyli a = 3 metry.
Krokiew to przeciwprostokątna, czyli 2a = 2 * 3 = 6 metrów.

Wskazówki i Triki

Zapamiętaj proporcje: Kluczem jest zapamiętanie proporcji a : a√3 : 2a.
Wizualizacja: Zawsze rysuj schemat, aby lepiej zrozumieć problem.
Uważaj na jednostki: Upewnij się, że wszystkie jednostki są spójne.
Sprawdź swoje obliczenia: Zawsze sprawdź, czy twoje wyniki mają sens w kontekście zadania.

Dlaczego Warto Znać Własności Trójkąta 30-60-90?

Znajomość właściwości trójkąta 30-60-90 to nie tylko przydatna umiejętność matematyczna. To również:

Szybsze rozwiązywanie zadań: Możesz uniknąć skomplikowanych obliczeń trygonometrycznych.
Lepsze zrozumienie geometrii: Pomaga w zrozumieniu relacji przestrzennych.
Praktyczne zastosowania: Przydatne w architekturze, inżynierii i wielu innych dziedzinach.
Podstawa do dalszej nauki: Zrozumienie tego trójkąta ułatwia zrozumienie bardziej zaawansowanych koncepcji matematycznych.

Podsumowanie

Trójkąt 30-60-90, choć na pierwszy rzut oka prosty, kryje w sobie potężne narzędzie do rozwiązywania problemów geometrycznych. Zapamiętanie proporcji między jego bokami – a : a√3 : 2a – otwiera drzwi do szybszych i łatwiejszych obliczeń. Niezależnie od tego, czy jesteś uczniem, studentem, inżynierem, czy po prostu entuzjastą matematyki, zrozumienie tego trójkąta z pewnością okaże się cenną umiejętnością.

Dzięki temu artykułowi dowiedzieliśmy się, dlaczego ten specyficzny trójkąt jest tak istotny, jak udowodnić jego właściwości i jak wykorzystywać go w praktycznych zastosowaniach. Mamy nadzieję, że zachęciliśmy Cię do dalszego zgłębiania tajników geometrii i odkrywania fascynującego świata matematyki! Pamiętaj, że regularna praktyka czyni mistrza!