Własności Liczb Naturalnych Zadania Klasa 8

Hej uczniowie! Witam was w przewodniku po własnościach liczb naturalnych, temat kluczowy w matematyce, a szczególnie istotny w klasie 8. Brzmi poważnie? Bez obaw! Rozłożymy to na czynniki pierwsze, obiecuję, że zrozumiecie wszystko krok po kroku. Zapomnijcie o skomplikowanych wzorach na chwilę – skupimy się na intuicji i przykładach z życia.

Czym są liczby naturalne?

Zacznijmy od podstaw. Liczby naturalne to po prostu liczby, których używamy do liczenia rzeczy. Wyobraźcie sobie, że macie przed sobą koszyk jabłek. Możecie powiedzieć: "Mam jedno jabłko", "Mam dwa jabłka", "Mam trzy jabłka" i tak dalej. Liczby 1, 2, 3, 4... to są właśnie liczby naturalne. Ważne: 0 *nie zawsze* jest uważane za liczbę naturalną. W niektórych kontekstach tak, w innych nie. Często używamy symbolu ℕ, aby oznaczyć zbiór liczb naturalnych, np. ℕ = {1, 2, 3, 4, ...} (lub ℕ = {0, 1, 2, 3, 4, ...}, zależnie od definicji).

Kluczowe cechy liczb naturalnych:

• Są to liczby całkowite. Nie ma ułamków ani liczb dziesiętnych.
• Są dodatnie (lub nieujemne, jeśli zero jest uwzględniane).
• Są używane do liczenia (czyli "counting numbers").

Myśląc o liczbach naturalnych, pomyślcie o schodach. Możecie wchodzić po kolejnych stopniach (1, 2, 3...), ale nie możecie stanąć pomiędzy nimi (np. na stopniu 2,5). To właśnie odróżnia liczby naturalne od innych rodzajów liczb.

Podzielność liczb naturalnych

Teraz przejdźmy do ważnej własności liczb naturalnych – podzielności. Mówimy, że liczba naturalna a jest podzielna przez liczbę naturalną b, jeśli wynik dzielenia a przez b jest liczbą naturalną (czyli nie ma reszty).

Przykład: 12 jest podzielne przez 3, bo 12 / 3 = 4, a 4 jest liczbą naturalną. Z kolei 13 nie jest podzielne przez 3, bo 13 / 3 = 4,333..., co nie jest liczbą naturalną.

Dzielniki i wielokrotności

Z podzielnością wiążą się dwa ważne pojęcia: dzielniki i wielokrotności.

• Dzielnik liczby a to liczba, przez którą a jest podzielna. Na przykład dzielnikami liczby 12 są: 1, 2, 3, 4, 6 i 12.
• Wielokrotność liczby b to liczba, która jest podzielna przez b. Na przykład wielokrotnościami liczby 3 są: 3, 6, 9, 12, 15 i tak dalej.

Wyobraźcie sobie, że macie 24 ciasteczka i chcecie je podzielić między kolegów. Dzielniki liczby 24 to liczby kolegów, między których możecie sprawiedliwie rozdzielić ciasteczka (bez krojenia ciasteczek!). Wielokrotności liczby 24 to liczby ciasteczek, które możecie mieć, jeśli kupicie kilka paczek po 24 ciasteczka każda.

Cechy podzielności

Istnieją pewne proste cechy podzielności, które ułatwiają sprawdzanie, czy dana liczba jest podzielna przez inną bez konieczności wykonywania dzielenia. Oto kilka z nich:

• Podzielność przez 2: Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra jest parzysta (0, 2, 4, 6 lub 8). Przykład: 124, 356, 1000.
• Podzielność przez 3: Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3. Przykład: 123 (1+2+3=6, a 6 jest podzielne przez 3), 456 (4+5+6=15, a 15 jest podzielne przez 3).
• Podzielność przez 4: Liczba jest podzielna przez 4, jeśli liczba utworzona przez jej dwie ostatnie cyfry jest podzielna przez 4. Przykład: 116 (16 jest podzielne przez 4), 2324 (24 jest podzielne przez 4).
• Podzielność przez 5: Liczba jest podzielna przez 5, jeśli jej ostatnia cyfra to 0 lub 5. Przykład: 25, 130, 1005.
• Podzielność przez 9: Liczba jest podzielna przez 9, jeśli suma jej cyfr jest podzielna przez 9. Przykład: 81 (8+1=9), 999 (9+9+9=27, a 27 jest podzielne przez 9).
• Podzielność przez 10: Liczba jest podzielna przez 10, jeśli jej ostatnia cyfra to 0. Przykład: 10, 120, 1500.

Pamiętajcie, że te cechy to tylko skróty. Zawsze możecie sprawdzić podzielność przez wykonanie dzielenia pisemnego.

Liczby pierwsze i złożone

Kolejne ważne pojęcia związane z liczbami naturalnymi to liczby pierwsze i liczby złożone.

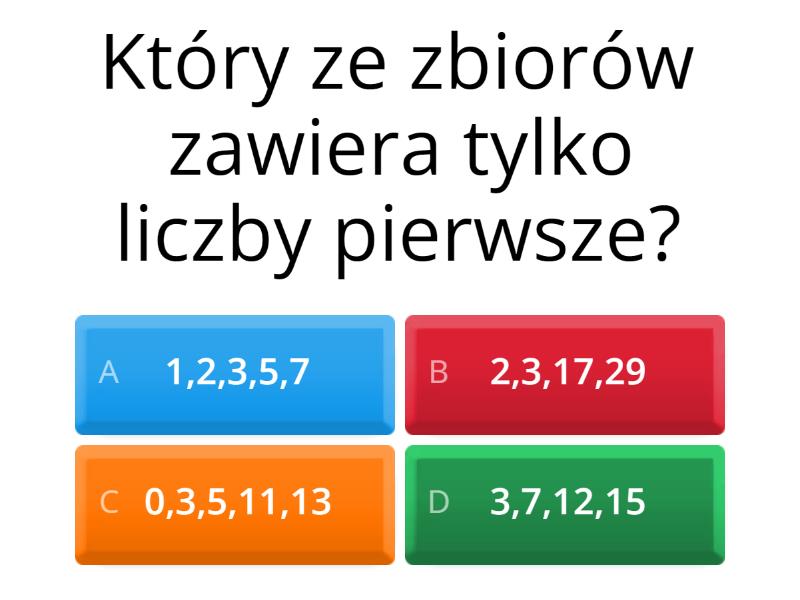
• Liczba pierwsza to liczba naturalna większa od 1, która ma tylko dwa dzielniki: 1 i samą siebie. Przykłady: 2, 3, 5, 7, 11, 13, 17...
• Liczba złożona to liczba naturalna większa od 1, która ma więcej niż dwa dzielniki. Przykłady: 4, 6, 8, 9, 10, 12, 14...

Liczba 1 nie jest ani pierwsza, ani złożona! Ma tylko jeden dzielnik (samą siebie).

Dlaczego liczby pierwsze są takie ważne? Są jak cegiełki, z których zbudowane są wszystkie inne liczby naturalne (oprócz 0 i 1). Każdą liczbę złożoną można rozłożyć na iloczyn liczb pierwszych – to się nazywa rozkład na czynniki pierwsze.

Przykład: Rozkład liczby 12 na czynniki pierwsze to 2 x 2 x 3 (czyli 2² x 3).

Przykłady z życia codziennego

Własności liczb naturalnych otaczają nas na każdym kroku! Oto kilka przykładów:

• Dzielenie słodyczy: Jeśli macie 15 cukierków i chcecie je sprawiedliwie podzielić między 5 przyjaciół, wykorzystujecie podzielność (15 podzielone przez 5 równa się 3).
• Układanie klocków: Jeśli macie pudełko klocków i chcecie zbudować wieżę, korzystacie z liczb naturalnych, aby liczyć klocki na każdym poziomie.
• Planowanie podróży: Obliczanie odległości, czasu podróży, kosztów paliwa – wszystko to opiera się na operacjach na liczbach naturalnych.
• Gotowanie: Przepisy wymagają odmierzenia składników, a to z kolei wiąże się z używaniem liczb naturalnych.

Zadania dla klasy 8

Teraz, gdy mamy solidne podstawy, możemy przejść do zadań typowych dla klasy 8. Oto kilka przykładów:

1. Znajdź wszystkie dzielniki liczby 36.
2. Sprawdź, czy liczba 248 jest podzielna przez 2, 3, 4, 5, 9 i 10.
3. Rozłóż liczbę 60 na czynniki pierwsze.
4. Znajdź największy wspólny dzielnik (NWD) liczb 24 i 36.
5. Znajdź najmniejszą wspólną wielokrotność (NWW) liczb 6 i 8.

Rozwiązując te zadania, wykorzystajcie wiedzę zdobytą w tym artykule. Pamiętajcie, że praktyka czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie własności liczb naturalnych.

Podsumowanie

Mam nadzieję, że ten artykuł pomógł wam zrozumieć własności liczb naturalnych. Pamiętajcie, że to tylko wstęp do fascynującego świata matematyki. Nie bójcie się zadawać pytań, eksperymentować i szukać własnych rozwiązań. Powodzenia!