Własności Figur Płaskich Klasa 8

Witaj w fascynującym świecie własności figur płaskich! Ten artykuł, skierowany do uczniów klasy 8, ma na celu uporządkowanie i pogłębienie Twojej wiedzy na temat podstawowych figur geometrycznych, które otaczają nas każdego dnia. Zrozumienie tych własności jest kluczowe nie tylko do rozwiązywania zadań z matematyki, ale także do lepszego postrzegania i analizowania otaczającego nas świata.

Przygotuj się na podróż przez świat trójkątów, kwadratów, prostokątów, równoległoboków, trapezów i kół! Zobaczymy, jakie cechy je wyróżniają, jak obliczać ich pola i obwody, a także gdzie te figury występują w życiu codziennym. Nie obawiaj się, nie będziemy zanudzać trudnymi definicjami. Zamiast tego postaramy się zrozumieć te zagadnienia intuicyjnie i praktycznie.

Podstawowe Figury Płaskie i Ich Własności

Trójkąty

Trójkąt to figura geometryczna, która ma trzy boki i trzy kąty. Istnieje wiele rodzajów trójkątów, a każdy z nich charakteryzuje się specyficznymi własnościami.

Podział trójkątów ze względu na boki:

Równoboczny: Wszystkie boki są równe, a wszystkie kąty mają miarę 60 stopni. Jest to trójkąt foremny.
Równoramienny: Dwa boki są równe (ramiona), a kąty przy podstawie są równe.
Różnoboczny: Wszystkie boki mają różne długości i wszystkie kąty mają różne miary.

Podział trójkątów ze względu na kąty:

Ostrokątny: Wszystkie kąty są ostre (mniejsze niż 90 stopni).
Prostokątny: Jeden kąt jest prosty (ma miarę 90 stopni). Bok leżący naprzeciwko kąta prostego nazywamy przeciwprostokątną, a pozostałe dwa boki to przyprostokątne.
Rozwartokątny: Jeden kąt jest rozwarty (większy niż 90 stopni).

Pole trójkąta obliczamy ze wzoru: P = (a * h) / 2, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę. Dla trójkąta prostokątnego pole można obliczyć jako połowę iloczynu długości przyprostokątnych: P = (a * b) / 2.

Obwód trójkąta to suma długości wszystkich jego boków: O = a + b + c.

Twierdzenie Pitagorasa obowiązuje w trójkącie prostokątnym: a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. To jedno z najważniejszych twierdzeń w geometrii!

Czworokąty

Czworokąt to figura geometryczna, która ma cztery boki i cztery kąty. Suma miar kątów wewnętrznych w czworokącie wynosi 360 stopni.

Do najważniejszych czworokątów należą:

Kwadrat: Wszystkie boki są równe, a wszystkie kąty są proste. Jest to czworokąt foremny.
Prostokąt: Ma cztery kąty proste. Przeciwległe boki są równe.
Równoległobok: Przeciwległe boki są równoległe i równe. Przeciwległe kąty są równe.
Romb: Wszystkie boki są równe. Przeciwległe kąty są równe. Przekątne przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy.
Trapez: Ma co najmniej jedną parę boków równoległych (podstawy). Trapez, który ma dwa nierównoległe boki równe, nazywamy trapezem równoramiennym.

Pole kwadratu: P = a², gdzie a to długość boku.

Pole prostokąta: P = a * b, gdzie a i b to długości boków.

Pole równoległoboku: P = a * h, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę.

Pole rombu: P = (d1 * d2) / 2, gdzie d1 i d2 to długości przekątnych. Można również obliczyć pole rombu jako P = a * h.

Pole trapezu: P = ((a + b) * h) / 2, gdzie a i b to długości podstaw, a h to wysokość.

Obwód kwadratu: O = 4 * a.

Obwód prostokąta: O = 2 * a + 2 * b.

Obwód równoległoboku: O = 2 * a + 2 * b.

Obwód rombu: O = 4 * a.

Obwód trapezu: O = a + b + c + d, gdzie a, b, c, i d to długości boków.

Koło i Okrąg

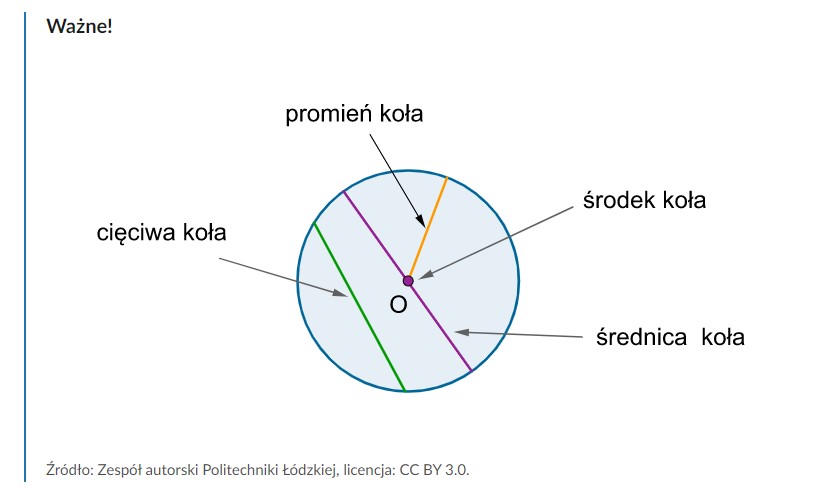
Okrąg to zbiór punktów na płaszczyźnie, które są równoodległe od ustalonego punktu, zwanego środkiem okręgu. Koło to obszar ograniczony okręgiem, wraz z okręgiem.

Promień okręgu (r) to odcinek łączący środek okręgu z dowolnym punktem na okręgu.

Średnica okręgu (d) to odcinek przechodzący przez środek okręgu i łączący dwa punkty na okręgu. Długość średnicy jest równa dwukrotnej długości promienia: d = 2r.

Liczba Pi (π) to stała matematyczna, która w przybliżeniu wynosi 3,14159. Jest to stosunek obwodu okręgu do jego średnicy.

Obwód okręgu (długość okręgu): O = 2 * π * r lub O = π * d.

Pole koła: P = π * r².

Przykłady z Życia Codziennego

Figury płaskie otaczają nas wszędzie. Oto kilka przykładów:

Trójkąty: Znaki drogowe (np. ostrzegawcze), dach domu, wieszaki.
Kwadraty i Prostokąty: Okna, drzwi, ekrany telewizorów i komputerów, zeszyty, książki, płytki podłogowe.
Równoległoboki: Niektóre znaki drogowe, wzory na tkaninach, układane kostki brukowe.
Koła: Koła samochodowe, tarcze zegarów, talerze, monety, pizzę.

Wyobraź sobie, że projektujesz swój pokój. Musisz obliczyć, ile farby potrzebujesz na pomalowanie ściany (prostokąt). Potrzebujesz wiedzieć, ile paneli podłogowych w kształcie prostokątów musisz kupić. Albo chcesz uszyć obrus na okrągły stół i musisz znać jego obwód. Zrozumienie własności figur płaskich jest kluczowe do rozwiązywania takich problemów!

Statystyki: Według badań przeprowadzonych przez Ministerstwo Edukacji Narodowej, uczniowie, którzy dobrze rozumieją geometrię, mają lepsze wyniki w innych dziedzinach matematyki i w przedmiotach ścisłych. Znajomość figur płaskich i umiejętność ich analizowania rozwija logiczne myślenie i wyobraźnię przestrzenną, co jest przydatne w wielu zawodach, takich jak architektura, inżynieria, grafika komputerowa czy projektowanie wnętrz.

Podsumowanie i Co Dalej?

Mam nadzieję, że ten artykuł pomógł Ci usystematyzować Twoją wiedzę na temat własności figur płaskich. Pamiętaj, że najważniejsze to praktyka! Rozwiązuj zadania, analizuj otaczające Cię przedmioty i staraj się dostrzegać w nich poznane figury geometryczne.

Co możesz zrobić dalej?

Wykorzystaj wiedzę zdobytą w tym artykule, aby rozwiązać zadania z podręcznika lub zbioru zadań.
Poszukaj w Internecie interaktywnych quizów i gier, które pomogą Ci utrwalić zdobytą wiedzę.
Spróbuj stworzyć własny projekt, w którym wykorzystasz różne figury płaskie, np. rysunek, mozaikę lub model 3D.
Porozmawiaj z nauczycielem matematyki, jeśli masz jakieś pytania lub wątpliwości.

Pamiętaj, że nauka geometrii może być fascynująca i przyjemna! Nie zrażaj się trudnościami, a z każdym rozwiązanym zadaniem poczujesz satysfakcję i zdobędziesz nowe umiejętności. Powodzenia!