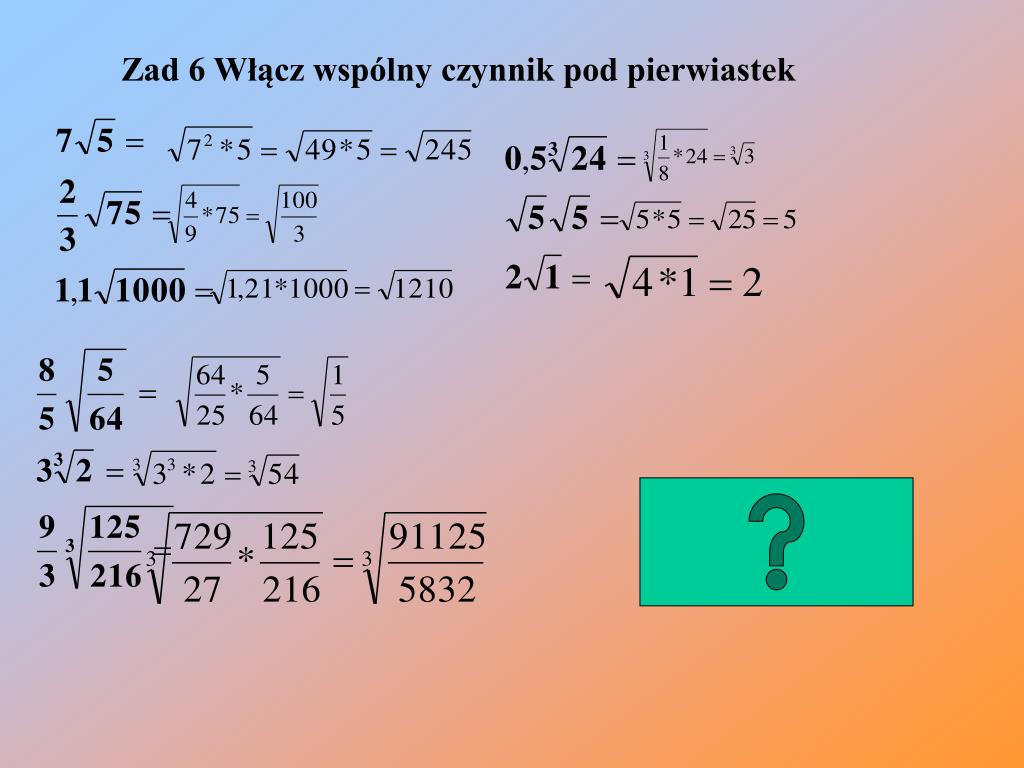Włącz Liczbę Pod Znak Pierwiastka

Czy kiedykolwiek patrzyłeś na wyrażenie z pierwiastkiem i czułeś się zagubiony, nie wiedząc, jak je uprościć? Jednym z fundamentalnych narzędzi w arsenale każdego adepta matematyki jest umiejętność wprowadzania liczby pod znak pierwiastka. Ten artykuł ma na celu demistyfikację tej techniki, czyniąc ją zrozumiałą i dostępną dla każdego, niezależnie od poziomu zaawansowania matematycznego. Skierowany jest do uczniów szkół podstawowych i średnich, maturzystów przygotowujących się do egzaminów, a także wszystkich osób, które chcą odświeżyć lub poszerzyć swoje umiejętności matematyczne. Nauczymy się, jak w prosty i efektywny sposób operować liczbami pod pierwiastkiem, co znacznie ułatwi rozwiązywanie różnorodnych zadań i problemów matematycznych.

Co to znaczy "Włączyć liczbę pod znak pierwiastka"?

Proces wprowadzania liczby pod znak pierwiastka to przekształcenie wyrażenia postaci a√b na postać √c, gdzie 'a' jest liczbą naturalną lub wymierną, którą "wciągamy" pod znak pierwiastka, a 'b' i 'c' są liczbami rzeczywistymi nieujemnymi. Innymi słowy, przenosimy liczbę znajdującą się przed pierwiastkiem pod ten pierwiastek, odpowiednio ją przekształcając.

Dlaczego to robimy? Umiejętność ta jest przydatna z kilku powodów:

• Upraszczanie wyrażeń: Czasami wprowadzenie liczby pod pierwiastek pozwala na uproszczenie skomplikowanych wyrażeń algebraicznych.
• Porównywanie liczb: Ułatwia porównywanie wielkości liczb wyrażonych za pomocą pierwiastków. Porównanie 2√3 i 3√2 staje się proste po wprowadzeniu liczb pod pierwiastek.
• Rozwiązywanie równań: W pewnych sytuacjach ułatwia manipulacje algebraiczne prowadzące do rozwiązania równań.
• Estetyka: Niektórym po prostu podoba się bardziej zwarta forma wyrażenia z pojedynczym pierwiastkiem.

Jak to zrobić – krok po kroku

Podstawowa zasada jest prosta: musimy podnieść liczbę, którą chcemy wprowadzić pod pierwiastek, do potęgi równej stopniowi pierwiastka. Następnie, wynik mnożymy przez liczbę znajdującą się już pod pierwiastkiem.

Pierwiastek kwadratowy (stopnia 2)

Najczęściej spotykany przypadek to pierwiastek kwadratowy. Jeśli mamy wyrażenie a√b, aby wprowadzić 'a' pod pierwiastek, musimy podnieść 'a' do kwadratu i pomnożyć przez 'b'. Czyli:

a√b = √(a² * b)

Przykład:

Weźmy wyrażenie 3√5. Chcemy wprowadzić 3 pod pierwiastek.

Krok 1: Podnosimy 3 do kwadratu: 3² = 9.

Krok 2: Mnożymy wynik przez liczbę pod pierwiastkiem: 9 * 5 = 45.

Zatem: 3√5 = √45.

Pierwiastek sześcienny (stopnia 3)

Analogicznie postępujemy w przypadku pierwiastka sześciennego. Jeżeli mamy a³√b, wtedy:

a³√b = ³√(a³ * b)

Przykład:

Weźmy wyrażenie 2³√7.

Krok 1: Podnosimy 2 do potęgi trzeciej: 2³ = 8.

Krok 2: Mnożymy wynik przez liczbę pod pierwiastkiem: 8 * 7 = 56.

Zatem: 2³√7 = ³√56.

Pierwiastek dowolnego stopnia

Ogólnie, dla pierwiastka stopnia 'n', mamy:

aⁿ√b = ⁿ√(aⁿ * b)

Przykład:

Weźmy wyrażenie 4⁴√2.

Krok 1: Podnosimy 4 do potęgi czwartej: 4⁴ = 256.

Krok 2: Mnożymy wynik przez liczbę pod pierwiastkiem: 256 * 2 = 512.

Zatem: 4⁴√2 = ⁴√512.

Praktyczne zastosowania i przykłady

Zobaczmy, jak możemy wykorzystać tę umiejętność w praktyce:

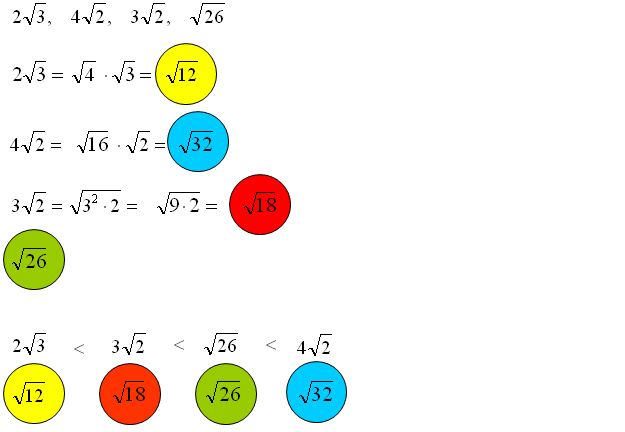
1. Porównywanie liczb: Która liczba jest większa: 2√3 czy 3√2?
• 2√3 = √(2² * 3) = √12
• 3√2 = √(3² * 2) = √18
• Ponieważ √18 > √12, to 3√2 > 2√3.
2. Upraszczanie wyrażeń: Uprość wyrażenie 5√2 + √50.
• Najpierw upraszczamy √50: √50 = √(25 * 2) = 5√2
• Teraz mamy: 5√2 + 5√2 = 10√2
• Możemy wprowadzić 10 pod pierwiastek: 10√2 = √(10² * 2) = √200
3. Rozwiązywanie równań: (Bardziej zaawansowany przykład, ale pokazuje potencjał) Rozwiąż równanie x = √(2√3)
• Możemy zapisać to jako x = √2 * √√3
• Wprowadźmy √2 pod "większy" pierwiastek: x = √(√2² * √3) = √(√4 * √3) = √(√12) = ⁴√12
• Podnosząc obie strony do potęgi czwartej otrzymujemy: x⁴ = 12, co pozwala na dalsze kroki w rozwiązaniu.

Na co uważać?

• Znaki: Jeżeli przed pierwiastkiem stoi liczba ujemna, to znak minus zostaje przed pierwiastkiem po wprowadzeniu liczby. Np. -2√5 = -√(2² * 5) = -√20.
• Ułamki: Technika działa również dla ułamków. Np. (1/2)√8 = √((1/2)² * 8) = √(1/4 * 8) = √2.
• Pamiętaj o stopniu pierwiastka: Kluczem jest podniesienie wprowadzanej liczby do potęgi równej stopniowi pierwiastka. Pomylenie stopnia pierwiastka to częsty błąd.

Ćwiczenia do samodzielnego wykonania

Aby utrwalić zdobytą wiedzę, spróbuj rozwiązać poniższe zadania:

1. Wprowadź liczbę pod pierwiastek:
• 4√3
• -2√7
• (1/3)√18
• 5³√2
2. Porównaj liczby:
• 4√2 i 2√8
• 3³√4 i 2³√9
3. Uprość wyrażenie i wprowadź liczbę pod pierwiastek:
• 2√5 + √20
• 3³√2 - ³√16

Rozwiązując te ćwiczenia, zdobędziesz pewność i biegłość w operowaniu liczbami pod pierwiastkiem. Pamiętaj, że praktyka czyni mistrza!

Podsumowanie

Umiejętność wprowadzania liczby pod znak pierwiastka to fundament w matematyce, otwierający drzwi do rozwiązywania bardziej złożonych problemów. Opanowanie tej techniki nie tylko ułatwi Ci radzenie sobie z zadaniami na lekcjach, ale również zwiększy Twoją pewność siebie w świecie matematyki. Mamy nadzieję, że ten artykuł okazał się pomocny i pozwolił Ci zrozumieć ten proces. Nie bój się eksperymentować i ćwiczyć, a z pewnością osiągniesz sukces! Powodzenia!