Wektor Przemieszczenia Cząstki Drugiej Względem Pierwszej

Zaczynamy więc naszą podróż w świat kinematyki i rozważmy sytuację, w której obserwujemy ruch dwóch punktów materialnych. Niech będą to cząstki A i B. Chcemy opisać, jak położenie cząstki B zmienia się w czasie z perspektywy cząstki A. To właśnie prowadzi nas do koncepcji wektora przemieszczenia cząstki B względem cząstki A.

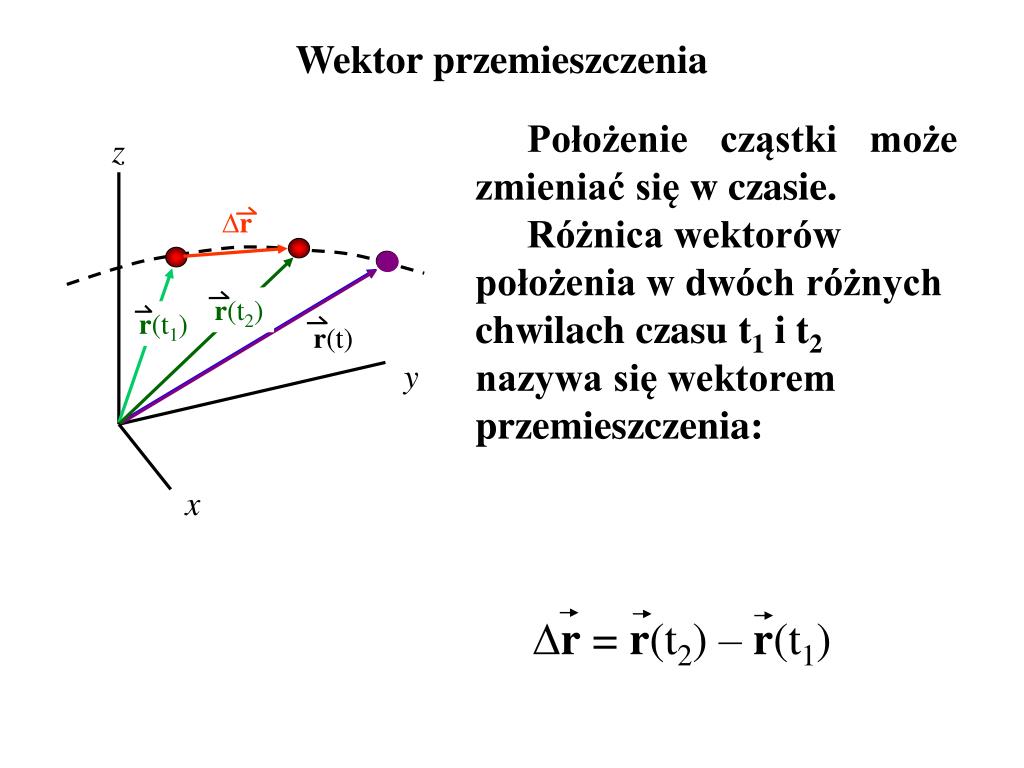
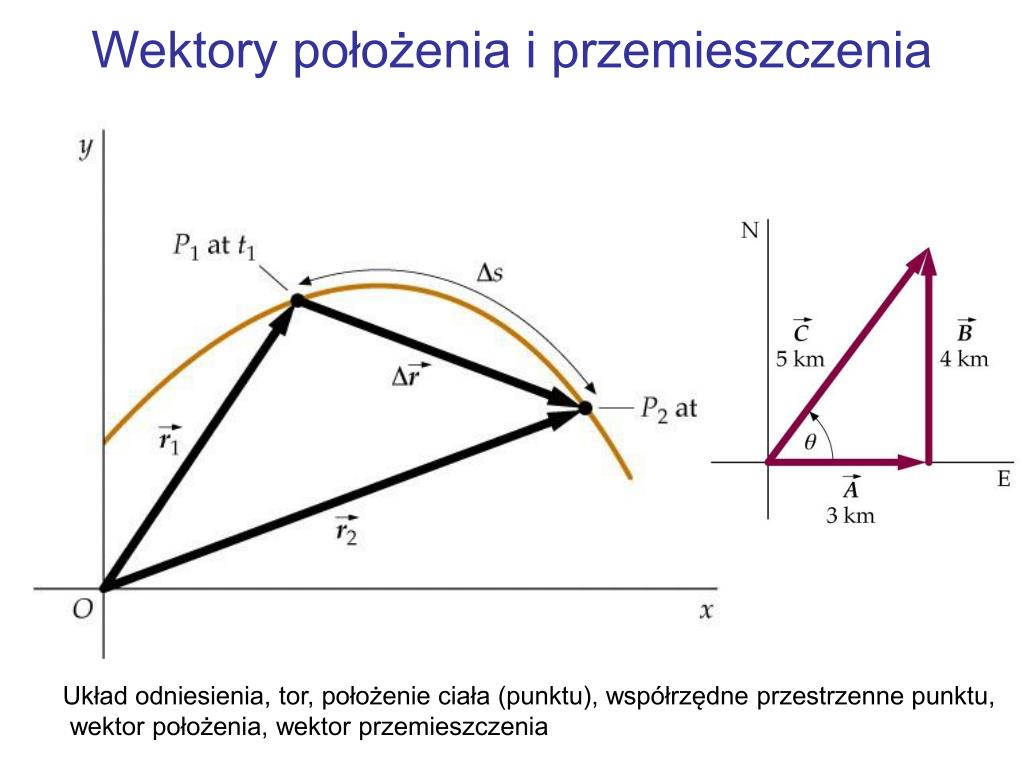
Wyobraźmy sobie układ współrzędnych, w którym obserwujemy ruch obu cząstek. W pewnej chwili czasu, powiedzmy t, cząstka A znajduje się w punkcie o wektorze położenia r_A(t), a cząstka B w punkcie o wektorze położenia r_B(t). Aby znaleźć wektor przemieszczenia cząstki B względem cząstki A, oznaczany zazwyczaj jako r_BA(t), odejmujemy wektor położenia cząstki A od wektora położenia cząstki B. Matematycznie, wyrażamy to jako:

r_BA(t) = r_B(t) - r_A(t)

Ten wektor, r_BA(t), wskazuje z punktu, w którym znajduje się cząstka A, do punktu, w którym znajduje się cząstka B, w danej chwili czasu t. Zauważmy, że r_BA(t) nie jest bezwzględnym położeniem cząstki B, ale raczej jej położeniem względem cząstki A.

Aby zrozumieć, jak to wygląda w praktyce, pomyślmy o dwóch samochodach jadących po autostradzie. Samochód A jedzie z prędkością 100 km/h, a samochód B jedzie z prędkością 120 km/h, oba w tym samym kierunku. Jeśli przyjmiemy, że na początku oba samochody znajdują się w tym samym miejscu, to po pewnym czasie, powiedzmy po godzinie, samochód B będzie o 20 km przed samochodem A. Wektor przemieszczenia samochodu B względem samochodu A będzie wektorem o długości 20 km skierowanym w kierunku ruchu. Z punktu widzenia kierowcy w samochodzie A, samochód B oddala się z prędkością 20 km/h.

Rozważmy teraz sytuację, w której samochody poruszają się w dwóch wymiarach. Niech samochód A jedzie na wschód z prędkością 80 km/h, a samochód B jedzie na północ z prędkością 60 km/h. Po jednej godzinie, samochód A będzie 80 km na wschód od punktu początkowego, a samochód B będzie 60 km na północ od punktu początkowego. Aby znaleźć wektor przemieszczenia samochodu B względem samochodu A, musimy wykonać odejmowanie wektorowe. Wektor położenia samochodu A po godzinie to (80 km, 0 km), a wektor położenia samochodu B po godzinie to (0 km, 60 km). Zatem wektor przemieszczenia samochodu B względem samochodu A to (0 km - 80 km, 60 km - 0 km) = (-80 km, 60 km). Długość tego wektora, czyli odległość między samochodami, można obliczyć za pomocą twierdzenia Pitagorasa: √((-80 km)² + (60 km)²) = √(6400 km² + 3600 km²) = √(10000 km²) = 100 km. Kierunek tego wektora, czyli kąt, pod jakim samochód B znajduje się względem samochodu A, można obliczyć za pomocą funkcji arcus tangens: arctan(60 km / -80 km) ≈ -36.87°. Ponieważ wektor leży w drugiej ćwiartce układu współrzędnych, musimy dodać 180° do tego kąta, aby uzyskać poprawny kąt: -36.87° + 180° = 143.13°. Zatem samochód B znajduje się 100 km od samochodu A pod kątem 143.13° względem osi wschodniej.

Prędkość Względna

Analogicznie do wektora przemieszczenia, możemy zdefiniować prędkość względną. Prędkość względna cząstki B względem cząstki A, oznaczana jako v_BA, to po prostu pochodna czasowa wektora przemieszczenia r_BA. Inaczej mówiąc, prędkość względna opisuje, jak szybko i w jakim kierunku zmienia się położenie cząstki B z punktu widzenia cząstki A. Matematycznie wyrażamy to jako:

v_BA(t) = dr_BA(t)/dt = d(r_B(t) - r_A(t))/dt = v_B(t) - v_A(t)

Gdzie v_B(t) to prędkość cząstki B w czasie t, a v_A(t) to prędkość cząstki A w czasie t. Zauważ, że prędkość względna to różnica wektorowa prędkości obu cząstek.

Wróćmy do przykładu z samochodami na autostradzie. Samochód A jedzie z prędkością 100 km/h, a samochód B jedzie z prędkością 120 km/h. Prędkość względna samochodu B względem samochodu A wynosi 120 km/h - 100 km/h = 20 km/h. Oznacza to, że z punktu widzenia kierowcy w samochodzie A, samochód B oddala się z prędkością 20 km/h.

A co w sytuacji, gdy samochody zbliżają się do siebie? Jeśli samochód A jedzie z prędkością 100 km/h w kierunku wschodnim, a samochód B jedzie z prędkością 80 km/h w kierunku zachodnim, to prędkość względna samochodu B względem samochodu A wynosi -80 km/h - 100 km/h = -180 km/h. Znak ujemny oznacza, że samochód B zbliża się do samochodu A. Z punktu widzenia kierowcy w samochodzie A, samochód B zbliża się z dużą prędkością 180 km/h.

Koncepcja prędkości względnej jest niezwykle przydatna w wielu sytuacjach, na przykład w nawigacji lotniczej i morskiej, gdzie konieczne jest uwzględnienie prędkości wiatru i prądów morskich. Pozwala na dokładne obliczanie kursów i przewidywanie pozycji obiektów.

Przyspieszenie Względne

Podobnie jak prędkość względną, możemy zdefiniować przyspieszenie względne. Przyspieszenie względne cząstki B względem cząstki A, oznaczane jako a_BA, to po prostu pochodna czasowa prędkości względnej v_BA. Inaczej mówiąc, przyspieszenie względne opisuje, jak szybko zmienia się prędkość cząstki B z punktu widzenia cząstki A. Matematycznie wyrażamy to jako:

a_BA(t) = dv_BA(t)/dt = d(v_B(t) - v_A(t))/dt = a_B(t) - a_A(t)

Gdzie a_B(t) to przyspieszenie cząstki B w czasie t, a a_A(t) to przyspieszenie cząstki A w czasie t. Zauważ, że przyspieszenie względne to różnica wektorowa przyspieszeń obu cząstek.

Załóżmy, że samochód A przyspiesza z 0 km/h do 100 km/h w 10 sekund, a samochód B przyspiesza z 0 km/h do 120 km/h w 10 sekund. Przyspieszenie samochodu A wynosi (100 km/h) / (10 s) = 10 km/h/s, a przyspieszenie samochodu B wynosi (120 km/h) / (10 s) = 12 km/h/s. Przyspieszenie względne samochodu B względem samochodu A wynosi 12 km/h/s - 10 km/h/s = 2 km/h/s. Oznacza to, że z punktu widzenia kierowcy w samochodzie A, samochód B przyspiesza w stosunku do niego o 2 km/h co sekundę.

Zrozumienie wektora przemieszczenia, prędkości i przyspieszenia względnego jest kluczowe do analizowania ruchu złożonych systemów, w których obiekty poruszają się względem siebie. Odgrywa ważną rolę w fizyce, inżynierii i wielu innych dziedzinach.

Podsumowując, wektor przemieszczenia cząstki B względem cząstki A dostarcza nam informacji o położeniu cząstki B z punktu widzenia obserwatora znajdującego się w cząstce A. Prędkość i przyspieszenie względne, odpowiednio, opisują tempo zmian tego położenia i prędkości. Pamiętajmy, że kluczem do zrozumienia tych koncepcji jest odejmowanie wektorowe. Zastosowanie tych narzędzi pozwala nam analizować ruch w bardziej złożonych i interesujących sytuacjach.