W Trójkącie Prostokątnym O Polu 49

Rozważania nad trójkątem prostokątnym o polu 49 jednostek stanowią interesujące zagadnienie z zakresu geometrii. Analiza właściwości takiego trójkąta, jego potencjalnych wymiarów i powiązań z innymi figurami geometrycznymi otwiera pole do wielu matematycznych eksploracji. Spróbujmy zgłębić tę tematykę, uwzględniając kluczowe aspekty i możliwości obliczeniowe.

Kluczowe Własności Trójkąta Prostokątnego

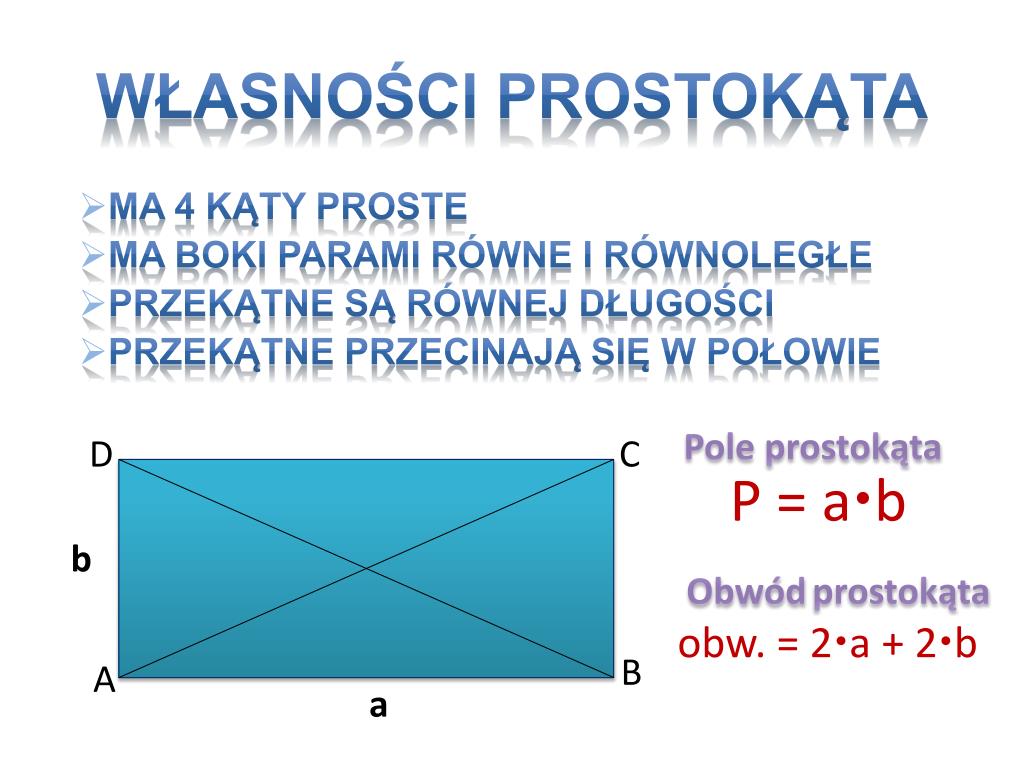
Trójkąt prostokątny charakteryzuje się obecnością jednego kąta prostego (90 stopni). Boki przylegające do tego kąta nazywane są przyprostokątnymi, natomiast bok leżący naprzeciwko kąta prostego to przeciwprostokątna. Pole trójkąta prostokątnego oblicza się jako połowę iloczynu długości jego przyprostokątnych.

Wzór na Pole i jego Implikacje

Wzór na pole trójkąta prostokątnego to P = (a * b) / 2, gdzie 'a' i 'b' oznaczają długości przyprostokątnych. Skoro mamy dany trójkąt o polu 49, to wiemy, że (a * b) / 2 = 49, co implikuje a * b = 98. Oznacza to, że iloczyn długości przyprostokątnych musi być równy 98.

Ta prosta równość otwiera wiele możliwości. Możemy znaleźć różne pary liczb, które pomnożone dają 98. Na przykład, jeśli a = 1, to b = 98. Jeśli a = 2, to b = 49. Jeśli a = 7, to b = 14. Każda z tych par definiuje inny trójkąt prostokątny o polu 49.

Twierdzenie Pitagorasa

Kolejnym kluczowym elementem związanym z trójkątem prostokątnym jest twierdzenie Pitagorasa, które mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej: a² + b² = c², gdzie 'c' oznacza długość przeciwprostokątnej. Wykorzystując tę zależność, możemy obliczyć długość przeciwprostokątnej dla dowolnych wartości 'a' i 'b' spełniających warunek a * b = 98.

Na przykład, jeśli a = 7 i b = 14, to c² = 7² + 14² = 49 + 196 = 245, a zatem c = √245 = 7√5. Zatem trójkąt o przyprostokątnych długości 7 i 14 ma przeciwprostokątną długości 7√5.

Możliwe Wymiary Trójkąta Prostokątnego o Polu 49

Znalezienie wszystkich możliwych wymiarów takiego trójkąta jest w zasadzie niemożliwe, ponieważ 'a' i 'b' mogą przyjmować wartości rzeczywiste. Jednak możemy znaleźć kilka całkowitoliczbowych przykładów:

• a = 1, b = 98, c = √(1² + 98²) = √9605
• a = 2, b = 49, c = √(2² + 49²) = √2405
• a = 7, b = 14, c = √(7² + 14²) = √245 = 7√5
• a = 14, b = 7, c = √(14² + 7²) = √245 = 7√5 (Trójkąt identyczny z poprzednim, tylko zamienione przyprostokątne)

Ważne jest, aby pamiętać, że istnieje nieskończenie wiele trójkątów prostokątnych o polu 49, ponieważ możemy wybrać dowolną wartość dla 'a' (różną od zera) i obliczyć 'b' jako 98/a. Dopiero nałożenie dodatkowych ograniczeń, takich jak całkowitoliczbowość boków, zawęża możliwe rozwiązania.

Powiązania z Innymi Figurami Geometrycznymi

Trójkąty prostokątne odgrywają fundamentalną rolę w geometrii i są często wykorzystywane w konstrukcjach i dowodach dotyczących innych figur. Przykładowo:

• Kwadrat wpisany w trójkąt: Można rozważać kwadrat, którego jeden bok leży na przeciwprostokątnej trójkąta, a dwa wierzchołki na przyprostokątnych. Istnieje zależność między bokiem kwadratu a wymiarami trójkąta.
• Okrąg wpisany w trójkąt: Można obliczyć promień okręgu wpisanego w trójkąt prostokątny o polu 49, wykorzystując wzory łączące pole, obwód i promień okręgu wpisanego.
• Okrąg opisany na trójkącie: W przypadku trójkąta prostokątnego, okrąg opisany ma środek w środku przeciwprostokątnej, a promień równy połowie długości przeciwprostokątnej.

Przykłady Zastosowań w Życiu Realnym

Choć zagadnienie trójkąta prostokątnego o polu 49 może wydawać się abstrakcyjne, ma ono zastosowania w różnych dziedzinach:

• Architektura i Budownictwo: Obliczanie powierzchni dachów, podłóg, czy ścian często wymaga rozkładu na prostsze figury, w tym trójkąty prostokątne. Znajomość relacji między bokami trójkąta pozwala na optymalizację konstrukcji i zużycia materiałów.
• Geodezja: Pomiar i mapowanie terenów wykorzystuje trójkąty prostokątne do wyznaczania odległości i wysokości. Techniki triangulacji opierają się na dokładnym pomiarze kątów i długości boków trójkątów.
• Nawigacja: Wyznaczanie pozycji za pomocą systemów GPS opiera się na obliczeniach geometrycznych, w których trójkąty prostokątne odgrywają kluczową rolę.
• Inżynieria: Projektowanie maszyn i urządzeń wymaga precyzyjnych obliczeń geometrycznych, w których wykorzystuje się właściwości trójkątów prostokątnych. Na przykład, obliczanie sił działających na dźwignie i inne elementy mechaniczne.

Wyobraźmy sobie, że projektujemy dach dwuspadowy. Jeżeli powierzchnia jednej połowy dachu (w kształcie trójkąta prostokątnego) ma wynosić 49 m², musimy dobrać odpowiednie wymiary (długość krokwy i szerokość podstawy) tak, aby spełnić ten warunek. Pozwala to na oszacowanie ilości materiałów potrzebnych do pokrycia dachu.

Wnioski i Dalsze Eksploracje

Analiza trójkąta prostokątnego o polu 49 jednostek pokazała, że istnieje nieskończenie wiele takich trójkątów, różniących się wymiarami. Kluczowe jest zrozumienie wzoru na pole trójkąta prostokątnego oraz twierdzenia Pitagorasa, które pozwalają na obliczanie długości boków. Dodatkowe warunki, takie jak całkowitoliczbowość boków, zawężają liczbę możliwych rozwiązań. Rozważania nad trójkątami prostokątnymi znajdują praktyczne zastosowania w wielu dziedzinach nauki i techniki.

Zachęcam do dalszego zgłębiania tematyki trójkątów prostokątnych, w tym do analizy ich powiązań z innymi figurami geometrycznymi, rozważania problemów optymalizacyjnych związanych z trójkątami prostokątnymi oraz poszukiwania zastosowań w konkretnych problemach inżynierskich i architektonicznych. Można również rozważyć analizę trójkątów prostokątnych o polu 49 i dodatkowych ograniczeniach, na przykład, gdy długości boków są liczbami całkowitymi i tworzą ciąg arytmetyczny.