W Pierwszej Wszystkie Są Dodatnie W Drugiej Tylko Sinus

W szkole średniej, na lekcjach matematyki, prędzej czy później natrafiamy na zagadnienie funkcji trygonometrycznych. Sinus, cosinus, tangens i cotangens – brzmią znajomo? Prawdopodobnie tak. Jednak często, w natłoku wzorów i definicji, umyka nam pewien prosty sposób, który pozwala na błyskawiczną orientację w znakach tych funkcji w zależności od ćwiartki układu współrzędnych, w której znajduje się dany kąt. Sposób ten, choć nieformalny i oparty na mnemonicznym skrócie, okazuje się niezwykle przydatny w rozwiązywaniu zadań i w zrozumieniu zależności pomiędzy kątem a wartością funkcji trygonometrycznych. Wyobraźmy sobie sytuację: mamy kąt 150 stopni. Bez kalkulatora, tylko z głową i wiedzą, musimy określić, czy sinus, cosinus i tangens tego kąta są dodatnie, czy ujemne. Brzmi strasznie? Spokojnie, wcale nie musi.

Najpierw przypomnijmy sobie układ współrzędnych. Mamy oś X (poziomą) i oś Y (pionową), które przecinają się w punkcie (0,0), zwanym początkiem układu współrzędnych. Te dwie osie dzielą płaszczyznę na cztery ćwiartki. Numerujemy je przeciwnie do ruchu wskazówek zegara, zaczynając od ćwiartki znajdującej się w prawym górnym rogu. Zatem:

Ćwiartka I: znajduje się w prawym górnym rogu.
Ćwiartka II: znajduje się w lewym górnym rogu.
Ćwiartka III: znajduje się w lewym dolnym rogu.
Ćwiartka IV: znajduje się w prawym dolnym rogu.

Teraz przejdźmy do sedna. Wyobraźmy sobie okrąg o promieniu 1, którego środek znajduje się w początku układu współrzędnych. Taki okrąg nazywamy okręgiem trygonometrycznym lub jednostkowym. Bierzemy dowolny kąt, powiedzmy θ (theta), i rysujemy go na tym okręgu. Ramię kąta zaczyna się na dodatniej półosi X i obraca się przeciwnie do ruchu wskazówek zegara. Punkt, w którym ramię kąta przecina okrąg jednostkowy, ma pewne współrzędne (x, y). I teraz magia:

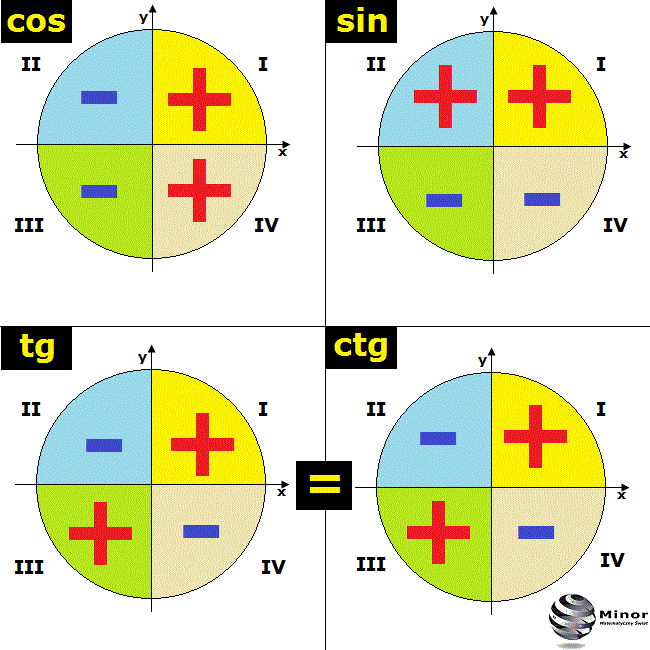
x jest wartością cosinusa kąta θ, czyli cos(θ) = x.
y jest wartością sinusa kąta θ, czyli sin(θ) = y.

To podstawowa definicja, która pozwala nam powiązać funkcje trygonometryczne z układem współrzędnych. No dobrze, ale co z tangensem i cotangensem? Tangens kąta to iloraz sinusa i cosinusa: tg(θ) = sin(θ) / cos(θ) = y / x. Natomiast cotangens to odwrotność tangensa, czyli iloraz cosinusa i sinusa: ctg(θ) = cos(θ) / sin(θ) = x / y.

Teraz, mając tę wiedzę, możemy przejść do zapamiętywania znaków funkcji trygonometrycznych w poszczególnych ćwiartkach.

Ćwiartki i Znaki Funkcji

W każdej ćwiartce układu współrzędnych współrzędne x i y mają różne znaki. W ćwiartce I zarówno x, jak i y są dodatnie. W ćwiartce II x jest ujemne, a y dodatnie. W ćwiartce III zarówno x, jak i y są ujemne. W ćwiartce IV x jest dodatnie, a y ujemne.

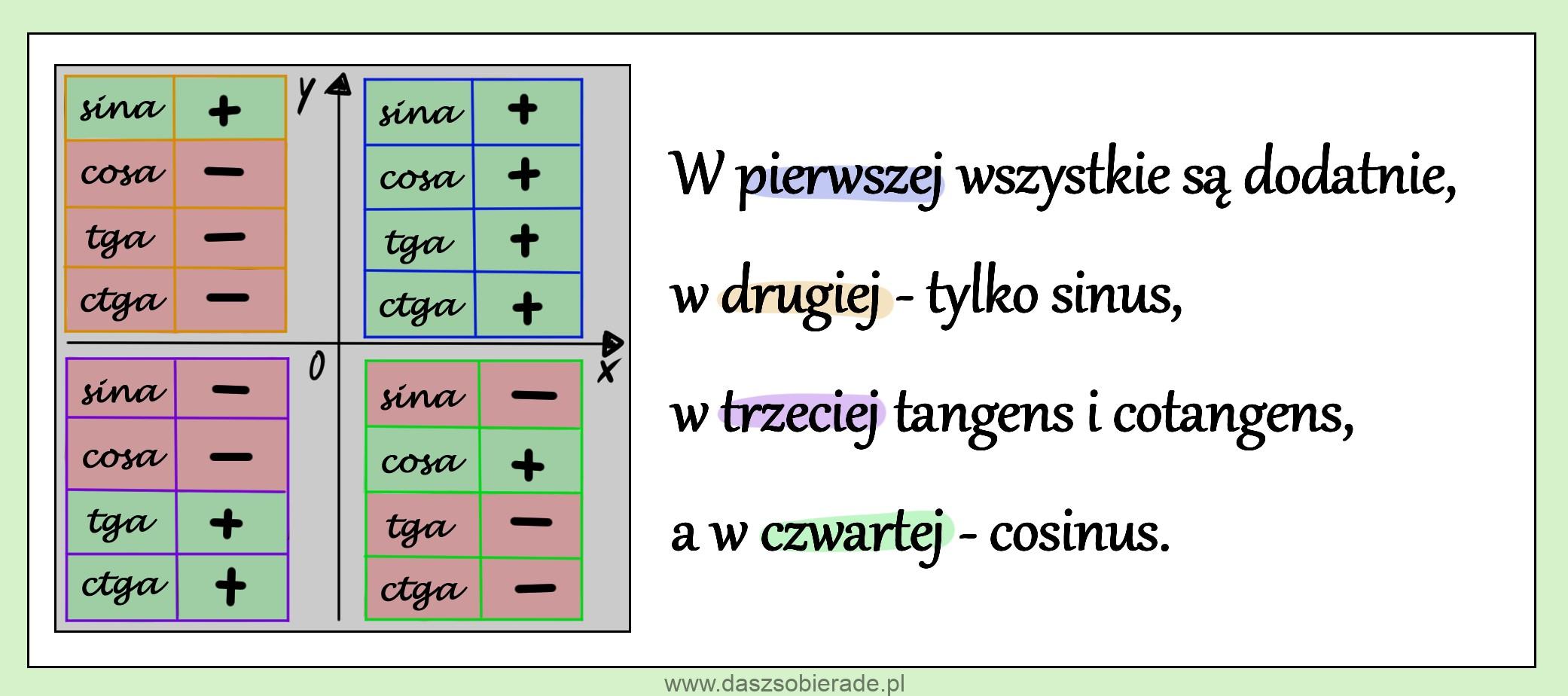
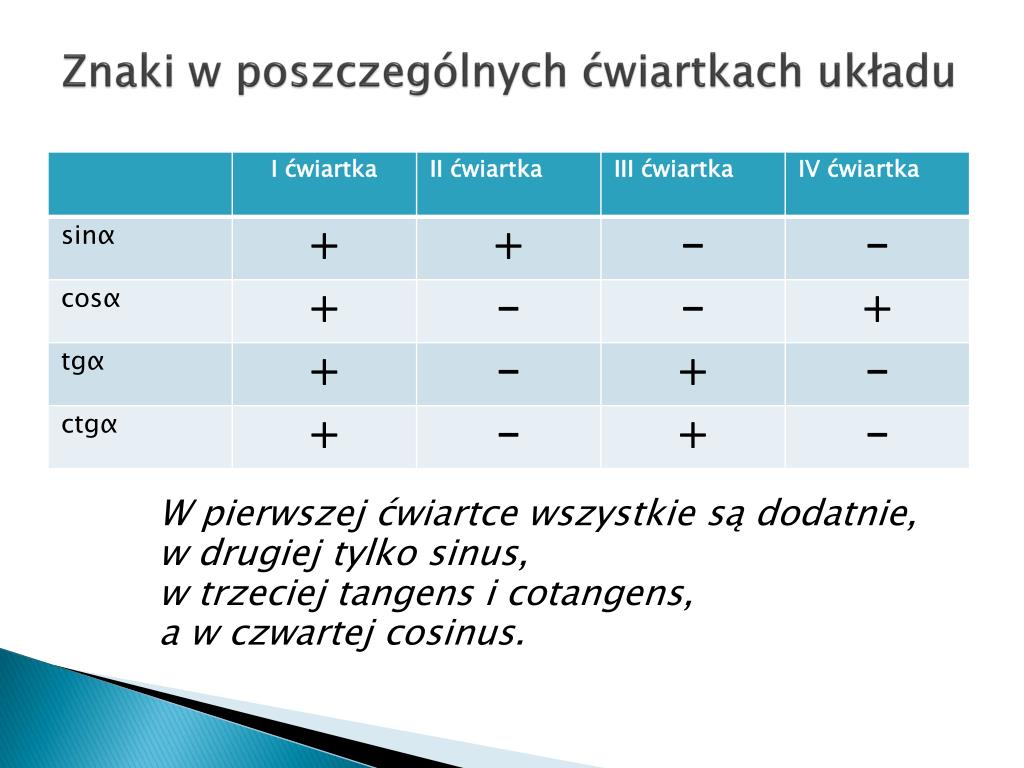
I tu pojawia się nasz skrót myślowy: "W pierwszej wszystkie są dodatnie, w drugiej tylko sinus". To prosty sposób na zapamiętanie, które funkcje trygonometryczne są dodatnie w poszczególnych ćwiartkach.

Ćwiartka I: Wszystkie funkcje (sinus, cosinus, tangens i cotangens) są dodatnie. Dlaczego? Bo x i y są dodatnie, więc ich ilorazy też są dodatnie.
Ćwiartka II: Tylko sinus jest dodatni. Dlaczego? Bo y (sinus) jest dodatni, a x (cosinus) jest ujemny. Zatem tangens i cotangens (które są ilorazami sinusa i cosinusa) są ujemne.
Ćwiartka III: Tangens i cotangens są dodatnie. Dlaczego? Bo x i y są ujemne, więc ich iloraz (tangens i cotangens) jest dodatni. Sinus i cosinus są ujemne.
Ćwiartka IV: Cosinus jest dodatni. Dlaczego? Bo x (cosinus) jest dodatni, a y (sinus) jest ujemny. Zatem tangens i cotangens są ujemne.

Możemy też zapamiętać to w ten sposób:

Ćwiartka I: Wszystkie (+)
Ćwiartka II: Sinus (+)
Ćwiartka III: Tangens i Cotangens (+)
Ćwiartka IV: Cosinus (+)

Albo jeszcze prościej: ASTC (All Students Take Calculus) - pierwsze litery nazw funkcji dodatnich w kolejnych ćwiartkach. To angielska wersja, ale łatwo zapada w pamięć. Można też wymyślić polski odpowiednik, np. "As Sympatyczny Tak Ciekawi" – cokolwiek, co ułatwi zapamiętanie.

Wracając do naszego przykładu: kąt 150 stopni leży w ćwiartce II (bo jest większy niż 90 stopni, ale mniejszy niż 180 stopni). Zatem sinus tego kąta jest dodatni, a cosinus i tangens są ujemne. Bez żadnych obliczeń, tylko na podstawie położenia kąta w układzie współrzędnych.

Inny przykład: kąt 240 stopni. Leży w ćwiartce III (bo jest większy niż 180 stopni, ale mniejszy niż 270 stopni). Zatem tangens i cotangens tego kąta są dodatnie, a sinus i cosinus są ujemne.

Wykorzystanie tej wiedzy w zadaniach jest bardzo proste. Załóżmy, że mamy równanie: sin(x) = -0.5 i wiemy, że x należy do przedziału (180 stopni, 270 stopni). Od razu wiemy, że szukamy kąta w ćwiartce III. Sinus jest tam ujemny, co zgadza się z równaniem. Wiemy, że sinus 30 stopni wynosi 0.5, a ponieważ w ćwiartce III sinus jest ujemny, nasz szukany kąt to 180 + 30 = 210 stopni.

Podsumowując, znajomość znaków funkcji trygonometrycznych w poszczególnych ćwiartkach układu współrzędnych jest niezwykle przydatna. Ułatwia rozwiązywanie zadań, pozwala na szybką orientację w problemie i eliminuje konieczność używania kalkulatora w wielu przypadkach. Pamiętając prosty skrót "W pierwszej wszystkie są dodatnie, w drugiej tylko sinus" (lub jego warianty), możemy w prosty sposób określić znak każdej funkcji trygonometrycznej dla dowolnego kąta. To jedna z tych "małych" rzeczy, które znacznie ułatwiają życie na lekcjach matematyki i podczas rozwiązywania zadań. Zatem, zapamiętaj i używaj!