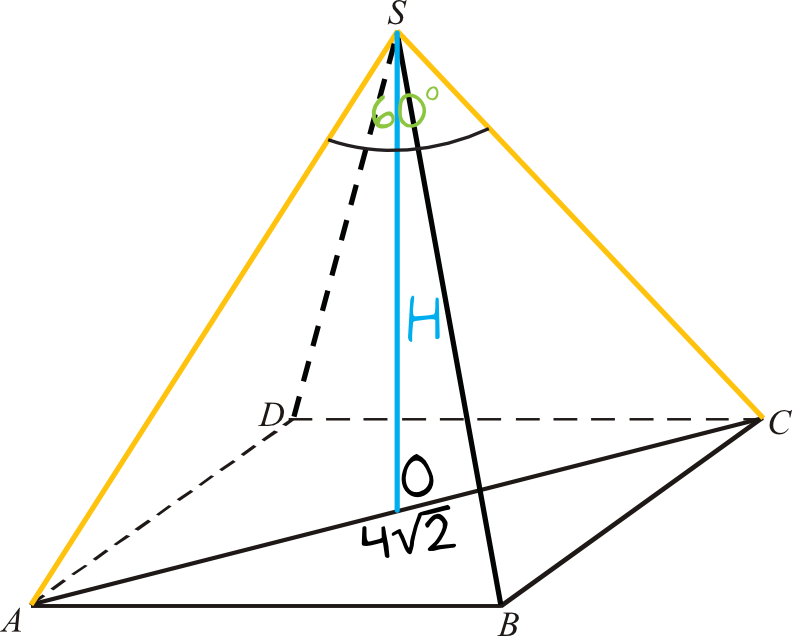
W Ostrosłupie Prawidłowym Czworokątnym Abcds Przekątna Ac

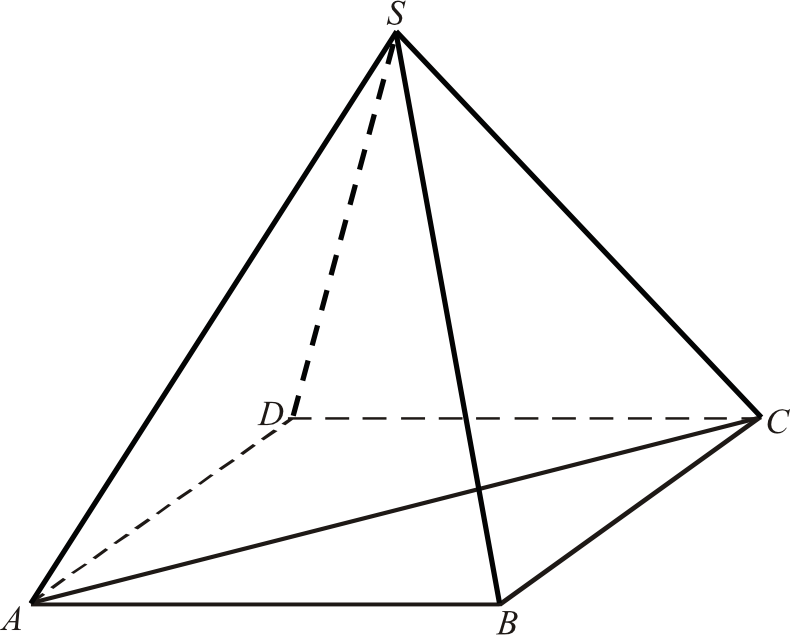
Okej, postaram się odpowiedzieć na pytanie o przekątną podstawy ostrosłupa prawidłowego czworokątnego ABCD. Wyjaśnię wszystko krok po kroku, tak żeby było to zrozumiałe.

Ostrosłup prawidłowy czworokątny to figura, która ma podstawę w kształcie kwadratu, a wszystkie ściany boczne są trójkątami równoramiennymi. Punkt, w którym zbiegają się wierzchołki tych trójkątów, to wierzchołek ostrosłupa. W naszym przypadku, podstawa to kwadrat ABCD, a wierzchołek ostrosłupa to punkt S. Zatem, rozważamy ostrosłup ABCDS. Interesuje nas długość przekątnej AC.

Czym jest przekątna w kwadracie?

Wyobraź sobie kwadrat. Ma cztery równe boki i cztery kąty proste. Przekątna to linia, która łączy dwa przeciwległe wierzchołki kwadratu, na przykład A i C, albo B i D. Przekątna dzieli kwadrat na dwa identyczne trójkąty prostokątne. To bardzo ważne, ponieważ możemy skorzystać z twierdzenia Pitagorasa, żeby obliczyć długość przekątnej.

Jak obliczyć długość przekątnej AC?

Załóżmy, że długość boku kwadratu ABCD wynosi a. Chcemy obliczyć długość przekątnej AC. Popatrz na trójkąt ABC. Jest to trójkąt prostokątny, gdzie kąt ABC jest kątem prostym. Boki AB i BC mają długość a, a bok AC to nasza szukana przekątna.

Teraz użyjemy twierdzenia Pitagorasa. Mówi ono, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych (czyli boków przylegających do kąta prostego) jest równa kwadratowi długości przeciwprostokątnej (czyli boku naprzeciwko kąta prostego).

W naszym przypadku:

AB² + BC² = AC²

Podstawiamy:

a² + a² = AC²

Upraszczamy:

2a² = AC²

Teraz wyciągamy pierwiastek kwadratowy z obu stron równania:

√(2a²) = √(AC²)

AC = a√2

Więc długość przekątnej AC kwadratu o boku a wynosi a√2. Oznacza to, że jeśli znasz długość boku kwadratu, wystarczy pomnożyć ją przez pierwiastek z 2, żeby otrzymać długość przekątnej.

Przykład

Powiedzmy, że bok kwadratu ABCD ma długość 5 cm. Wtedy długość przekątnej AC wynosi:

AC = 5√2 cm

W przybliżeniu, pierwiastek z 2 to około 1.41. Zatem:

AC ≈ 5 * 1.41 cm ≈ 7.05 cm

Długość przekątnej AC wynosi około 7.05 cm.

Podsumowanie

W ostrosłupie prawidłowym czworokątnym ABCD**, gdzie ABCD jest podstawą będącą kwadratem o boku a, długość przekątnej AC można obliczyć ze wzoru:

AC = a√2

Znając długość boku kwadratu, łatwo znajdziesz długość przekątnej. Pamiętaj, że przekątna dzieli kwadrat na dwa trójkąty prostokątne, co pozwala na użycie twierdzenia Pitagorasa. To bardzo przydatne narzędzie w geometrii.

Jeśli bok kwadratu jest dany, po prostu pomnóż jego długość przez pierwiastek kwadratowy z 2, a otrzymasz długość przekątnej. To proste, prawda?