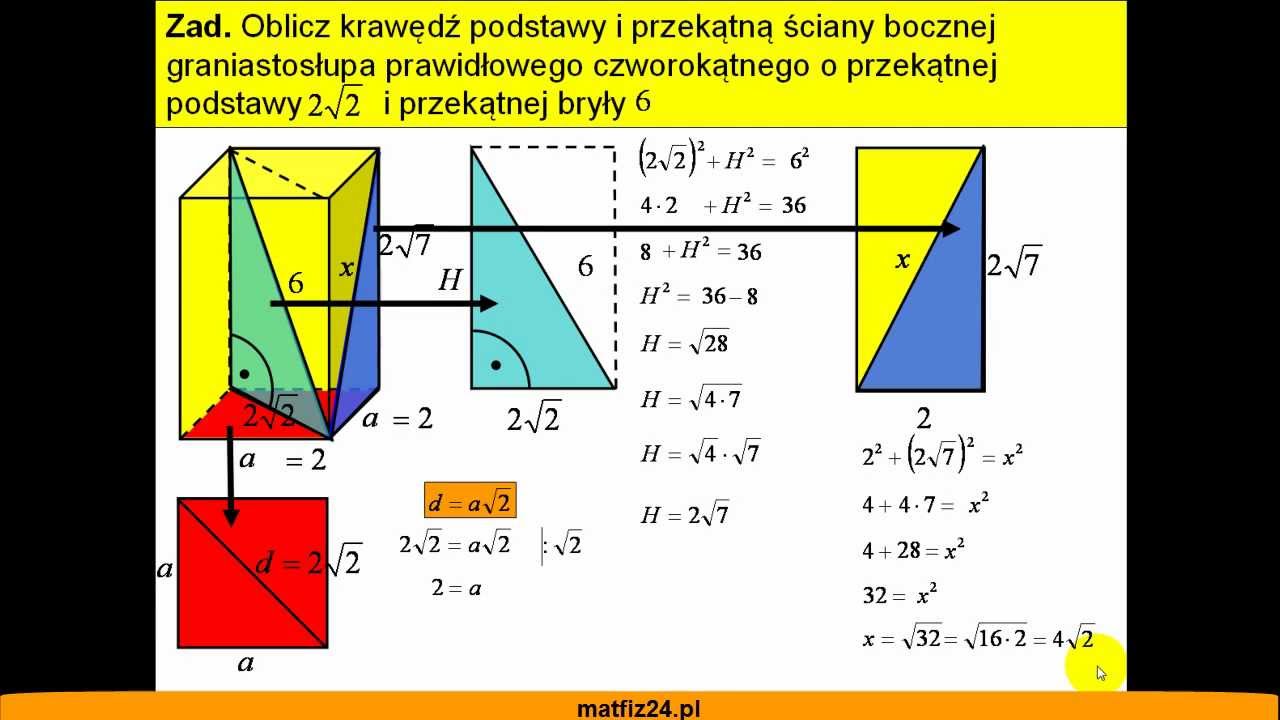
W Graniastosłupie Prawidłowym Czworokątnym Abcdefgh Przekątna Ac

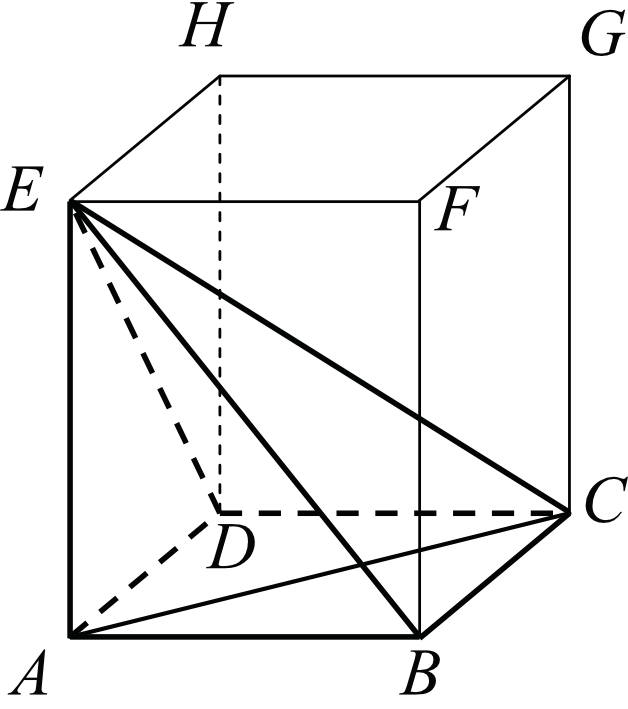
Witajcie! Dziś zagłębimy się w fascynujący świat geometrii, a konkretnie skupimy się na graniastosłupie prawidłowym czworokątnym. Wyobraźmy sobie graniastosłup ABCDEFGH, a naszą szczególną uwagę poświęcimy przekątnej AC. Przygotujcie się na podróż pełną wzorów, zależności i intrygujących właściwości.

Zaczynamy od definicji. Graniastosłup prawidłowy czworokątny to graniastosłup prosty, którego podstawą jest kwadrat. Oznacza to, że wszystkie jego ściany boczne są prostokątami, a krawędzie boczne są prostopadłe do płaszczyzn podstaw. W naszym przypadku, podstawa ABCD jest kwadratem, podobnie jak podstawa EFGH.

Teraz skupmy się na przekątnej AC. Jest to przekątna kwadratu ABCD. Aby obliczyć jej długość, wykorzystamy twierdzenie Pitagorasa. Niech długość boku kwadratu ABCD wynosi 'a'. Wówczas trójkąt ABC jest trójkątem prostokątnym, gdzie kąt ABC jest kątem prostym. Zatem:

|AC|^2 = |AB|^2 + |BC|^2

Ponieważ |AB| = |BC| = a, otrzymujemy:

|AC|^2 = a^2 + a^2 = 2a^2

Wyciągając pierwiastek kwadratowy z obu stron, otrzymujemy:

|AC| = √(2a^2) = a√2

Zatem długość przekątnej AC kwadratu ABCD wynosi a√2. To bardzo ważny wzór, który często wykorzystujemy w zadaniach geometrycznych.

Zastanówmy się teraz, jak obecność graniastosłupa wpływa na nasze rozważania. Przekątna AC jest częścią kwadratu podstawy, a zatem jej długość pozostaje niezależna od wysokości graniastosłupa. Wysokość graniastosłupa, oznaczmy ją jako 'h', wpływa na inne przekątne i zależności w całej bryle, ale nie na długość AC.

Spójrzmy na przekątną ścianę boczną. Na przykład, rozważmy ścianę boczną ABFE. Jest to prostokąt o bokach długości 'a' i 'h'. Przekątna tej ściany, na przykład AF, może być obliczona również przy użyciu twierdzenia Pitagorasa:

|AF|^2 = |AB|^2 + |BF|^2 = a^2 + h^2

Zatem |AF| = √(a^2 + h^2). Widzimy, że długość przekątnej ściany bocznej zależy już od wysokości graniastosłupa.

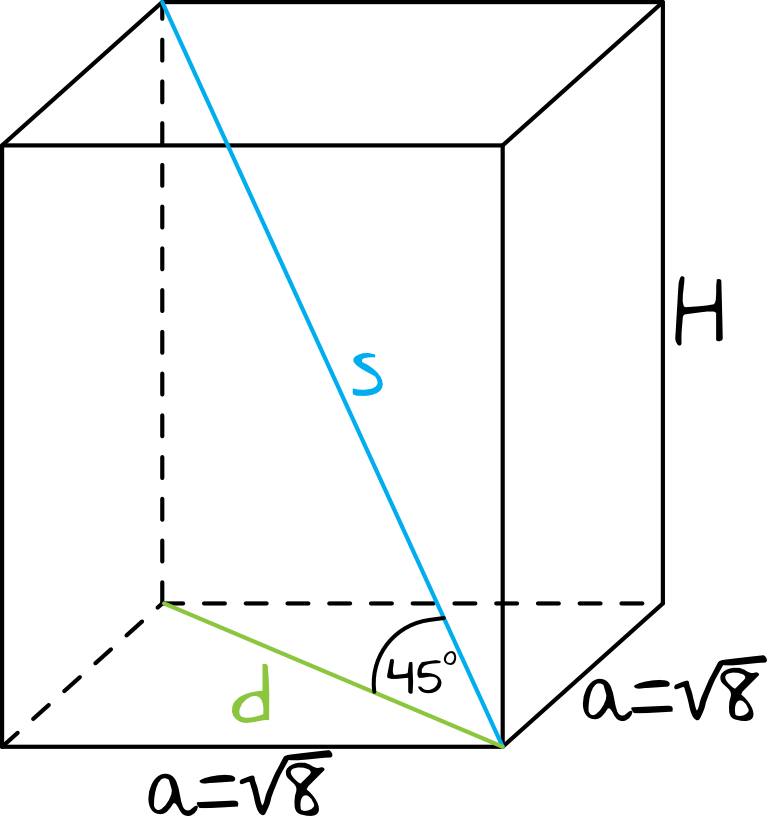
Możemy także rozważyć przekątną całego graniastosłupa, na przykład AG. Aby ją obliczyć, możemy wykorzystać trójkąt prostokątny ACG, gdzie kąt ACG jest kątem prostym. Znamy długość AC (a√2) i długość CG (h). Zatem:

|AG|^2 = |AC|^2 + |CG|^2 = (a√2)^2 + h^2 = 2a^2 + h^2

Stąd |AG| = √(2a^2 + h^2). W tym przypadku również widzimy, że długość przekątnej graniastosłupa zależy od zarówno długości boku podstawy, jak i wysokości graniastosłupa.

Związek Przekątnej AC z Powierzchnią i Objętością

Przekątna AC, choć sama w sobie jest elementem dwuwymiarowym (odcinkiem na płaszczyźnie), ma wpływ na różne parametry opisujące cały graniastosłup. Związek ten jest pośredni, ale warto go zrozumieć.

Powierzchnia całkowita graniastosłupa prawidłowego czworokątnego składa się z dwóch powierzchni podstaw oraz czterech powierzchni ścian bocznych. Powierzchnia jednej podstawy to a^2. Powierzchnia jednej ściany bocznej to a*h. Zatem powierzchnia całkowita (Pc) wynosi:

Pc = 2 * a^2 + 4 * a * h = 2a^2 + 4ah

Widzimy, że długość boku podstawy 'a', która determinuje długość przekątnej AC, jest kluczowym elementem w obliczaniu powierzchni całkowitej. Jeśli znamy długość AC, możemy obliczyć długość boku 'a' jako a = |AC| / √2, a następnie podstawić to do wzoru na pole powierzchni.

Objętość graniastosłupa (V) obliczamy mnożąc pole podstawy przez wysokość:

V = a^2 * h

Ponownie, długość boku podstawy 'a' odgrywa zasadniczą rolę. Znamy AC, wyliczamy 'a', i możemy obliczyć objętość, jeśli znamy również wysokość 'h'.

Przekątna AC w Zadaniach Geometrycznych

Przyjrzyjmy się teraz, jak wiedza o przekątnej AC przydaje się w rozwiązywaniu zadań geometrycznych. Zadania związane z graniastosłupami prawidłowym czworokątnymi często wymagają znajomości zależności między różnymi elementami, takimi jak długość krawędzi, wysokość, przekątne ścian, przekątne bryły, powierzchnia i objętość.

Przykład 1: Załóżmy, że mamy graniastosłup prawidłowy czworokątny ABCDEFGH, w którym przekątna AC ma długość 5√2 cm, a wysokość graniastosłupa wynosi 8 cm. Oblicz objętość graniastosłupa.

Rozwiązanie: Znamy |AC| = 5√2 cm. Zatem a = |AC| / √2 = (5√2) / √2 = 5 cm. Wysokość graniastosłupa h = 8 cm. Objętość V = a^2 * h = 5^2 * 8 = 25 * 8 = 200 cm^3.

Przykład 2: W graniastosłupie prawidłowym czworokątnym ABCDEFGH, pole podstawy wynosi 16 cm^2. Oblicz długość przekątnej AC.

Rozwiązanie: Pole podstawy to a^2 = 16 cm^2. Zatem a = √16 = 4 cm. Długość przekątnej AC = a√2 = 4√2 cm.

Przykład 3: Przekątna graniastosłupa prawidłowego czworokątnego ABCDEFGH ma długość 13 cm, a wysokość wynosi 12 cm. Oblicz długość przekątnej AC.

Rozwiązanie: Znamy |AG| = 13 cm oraz h = 12 cm. Zatem |AG|^2 = 2a^2 + h^2. Podstawiając wartości, otrzymujemy: 13^2 = 2a^2 + 12^2. 169 = 2a^2 + 144. 2a^2 = 25. a^2 = 12.5. a = √12.5 = √(25/2) = 5/√2 = (5√2)/2. Zatem |AC| = a√2 = ((5√2)/2) * √2 = (5 * 2) / 2 = 5 cm.

Przekątna AC, choć wydaje się być prostym elementem kwadratu podstawy, jest kluczowym ogniwem łączącym różne aspekty graniastosłupa. Rozumienie jej relacji z innymi elementami pozwala na sprawne rozwiązywanie zadań i pełniejsze zrozumienie geometrii przestrzennej. Mam nadzieję, że ta podróż po świecie graniastosłupa prawidłowego czworokątnego była dla Was pouczająca i inspirująca. Pamiętajcie, że geometria to nie tylko wzory, ale przede wszystkim logiczne myślenie i umiejętność dostrzegania zależności. Powodzenia w dalszej nauce!