Uzupełnij Tabelę A Bok Kwadratu

Czy kiedykolwiek zastanawiałeś się, jak powiązać długość boku kwadratu z jego obwodem, polem czy długością przekątnej? Kwadrat, ta fundamentalna figura geometryczna, kryje w sobie wiele prostych, ale potężnych zależności. W tym artykule, przeznaczonym zarówno dla uczniów przygotowujących się do egzaminów, jak i dla wszystkich entuzjastów matematyki, zajmiemy się uzupełnianiem tabeli dotyczącej kwadratu, odkrywając te zależności krok po kroku. Przygotuj się na fascynującą podróż po świecie geometrii!
Zrozumienie podstawowych właściwości kwadratu
Zanim przystąpimy do uzupełniania tabeli, upewnijmy się, że doskonale rozumiemy definicję i podstawowe własności kwadratu. Kwadrat to czworokąt, który spełnia dwa kluczowe warunki: wszystkie jego boki są równej długości, a wszystkie jego kąty są proste (mają miarę 90 stopni). Z tych dwóch prostych faktów wynikają wszystkie inne własności, które będziemy wykorzystywać. Pomyśl o kafelku w łazience – najczęściej jest on właśnie kwadratowy.
Kluczowe własności kwadratu:
- Równe boki: Oznaczmy długość boku kwadratu jako 'a'.
- Kąty proste: Każdy z czterech kątów ma miarę 90 stopni.
- Przekątne: Przekątne kwadratu są równej długości, przecinają się pod kątem prostym i dzielą się na połowy.
- Symetria: Kwadrat posiada wysoką symetrię – cztery osie symetrii.
Jak uzupełnić tabelę związaną z bokiem kwadratu?
Załóżmy, że mamy tabelę, w której w pierwszej kolumnie podane są różne długości boków kwadratu, a w kolejnych kolumnach musimy obliczyć obwód, pole i długość przekątnej. Pokażemy teraz, jak to zrobić, krok po kroku.
Obwód kwadratu
Obwód kwadratu to suma długości wszystkich jego boków. Ponieważ wszystkie boki kwadratu mają długość 'a', obwód (O) obliczamy ze wzoru:
O = 4a
Przykładowo, jeśli bok kwadratu ma długość 5 cm, to jego obwód wynosi:
O = 4 * 5 cm = 20 cm
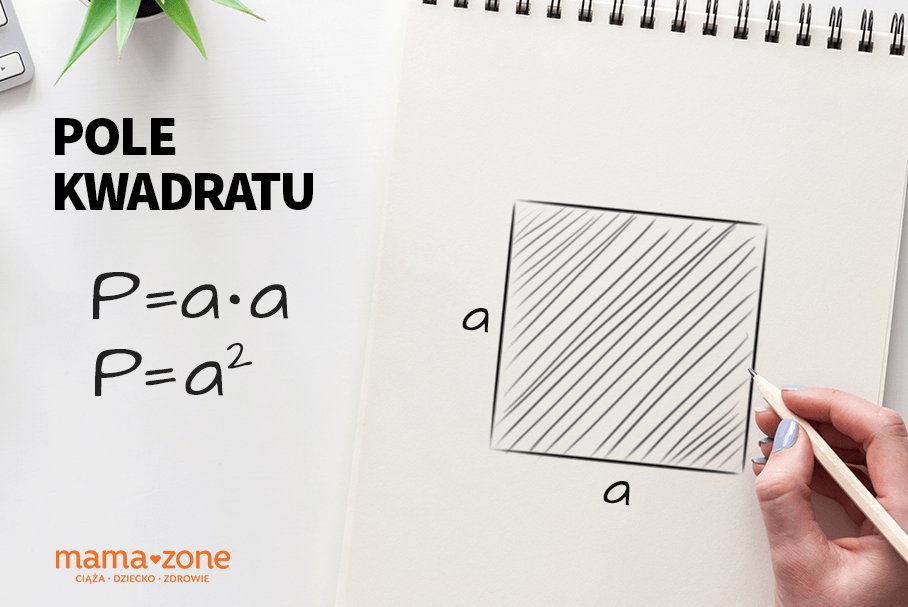
Pole kwadratu
Pole kwadratu to obszar, który zajmuje kwadrat na płaszczyźnie. Obliczamy je, mnożąc długość boku przez długość boku:
P = a2
Używając tego samego przykładu, jeśli bok kwadratu ma długość 5 cm, to jego pole wynosi:
P = (5 cm)2 = 25 cm2
Długość przekątnej kwadratu
Przekątna kwadratu łączy dwa przeciwległe wierzchołki. Możemy ją obliczyć, korzystając z twierdzenia Pitagorasa (a2 + b2 = c2) lub ze wzoru wynikającego bezpośrednio z tego twierdzenia dla kwadratu:
d = a√2
Gdzie 'd' to długość przekątnej, a 'a' to długość boku kwadratu.
Dla boku o długości 5 cm, przekątna wynosi:
d = 5 cm * √2 ≈ 5 cm * 1.41 ≈ 7.05 cm
Przykładowa tabela i jej uzupełnienie
Oto przykładowa tabela, którą możemy uzupełnić:
| Długość boku (a) | Obwód (O) | Pole (P) | Długość przekątnej (d) |
|---|---|---|---|
| 3 cm | 12 cm | 9 cm2 | 3√2 cm ≈ 4.23 cm |
| 7 cm | 28 cm | 49 cm2 | 7√2 cm ≈ 9.90 cm |
| 10 cm | 40 cm | 100 cm2 | 10√2 cm ≈ 14.14 cm |
| 1.5 cm | 6 cm | 2.25 cm2 | 1.5√2 cm ≈ 2.12 cm |
| 0.5 cm | 2 cm | 0.25 cm2 | 0.5√2 cm ≈ 0.71 cm |
Jak widać, wypełnienie tabeli jest proste, pod warunkiem, że pamiętamy odpowiednie wzory. Kluczem jest systematyczne podstawianie wartości długości boku do każdego wzoru i wykonanie obliczeń.
Praktyczne zastosowania wiedzy o kwadracie
Wiedza o właściwościach kwadratu i umiejętność obliczania jego obwodu, pola i przekątnej, choć wydaje się abstrakcyjna, ma wiele praktycznych zastosowań w życiu codziennym oraz w różnych dziedzinach nauki i techniki. Oto kilka przykładów:
- Budownictwo i architektura: Obliczanie ilości materiałów potrzebnych do pokrycia kwadratowej powierzchni (np. płytek, paneli), planowanie przestrzeni, projektowanie elewacji budynków.
- Projektowanie graficzne: Tworzenie logo, projektowanie układów stron internetowych, tworzenie ikon i grafik.
- Inżynieria: Obliczanie wytrzymałości elementów konstrukcyjnych o kwadratowym przekroju, projektowanie maszyn i urządzeń.
- Rzemiosło: Wycinanie tkanin, papieru, drewna w kształcie kwadratów, projektowanie i wykonywanie mebli.
- Gry i zabawy: Projektowanie plansz do gier, tworzenie puzzli, rozwiązywanie łamigłówek geometrycznych.
Wyobraź sobie, że planujesz położyć płytki w kształcie kwadratów w łazience. Musisz obliczyć, ile płytek potrzebujesz, aby pokryć całą podłogę. Znając wymiary podłogi i płytek, możesz łatwo obliczyć pole powierzchni podłogi i pole powierzchni jednej płytki, a następnie podzielić jedno przez drugie, aby otrzymać liczbę potrzebnych płytek. To proste zadanie wymaga jednak znajomości wzoru na pole kwadratu!
Wskazówki i triki
- Pamiętaj o jednostkach: Zawsze upewnij się, że wszystkie wymiary są podane w tej samej jednostce (np. centymetry, metry). Jeśli tak nie jest, przekształć je przed rozpoczęciem obliczeń.
- Sprawdzaj wyniki: Po obliczeniu obwodu, pola lub przekątnej, zastanów się, czy wynik jest sensowny. Czy obwód jest większy niż długość boku? Czy pole jest wyrażone w jednostkach kwadratowych?
- Korzystaj z kalkulatora: Do obliczeń z pierwiastkiem kwadratowym (√2) warto użyć kalkulatora, aby uzyskać dokładniejszy wynik.
- Zapamiętaj wzory: Im lepiej zapamiętasz wzory na obwód, pole i przekątną kwadratu, tym szybciej i łatwiej będziesz mógł rozwiązywać zadania.
- Ćwicz: Rozwiązuj jak najwięcej zadań związanych z kwadratami, aby utrwalić wiedzę i nabrać wprawy.
Podsumowanie
Uzupełnianie tabeli z danymi kwadratu, choć na pierwszy rzut oka może wydawać się prostym zadaniem, pomaga zrozumieć fundamentalne zależności geometryczne. Znajomość wzorów na obwód, pole i długość przekątnej oraz umiejętność ich stosowania jest niezwykle przydatna zarówno w szkole, jak i w życiu codziennym. Mamy nadzieję, że ten artykuł pozwolił Ci lepiej zrozumieć te zależności i poczuć się pewniej w rozwiązywaniu zadań związanych z kwadratami. Pamiętaj, że kluczem do sukcesu jest praktyka – im więcej ćwiczysz, tym lepiej będziesz rozumiał i zapamiętywał! Powodzenia!